No mundo real, as oscilações raramente seguem o verdadeiro SHM. A fricção de algum tipo geralmente actua para amortecer o movimento, de modo que este morre, ou precisa de mais força para continuar. Nesta secção, examinamos alguns exemplos de movimento harmónico amortecido e vemos como modificar as equações de movimento para descrever este caso mais geral.

Uma corda de guitarra deixa de oscilar alguns segundos depois de ser depenada. Para continuar a oscilar no balanço de um playground, é preciso continuar a empurrar (Figura \PageIndex{1}}). Embora possamos frequentemente tornar o atrito e outras forças não conservadoras pequenas ou insignificantes, o movimento completamente não amortecido é raro. De facto, podemos até querer amortecer oscilações, tais como com amortecedores de choque automóvel.

Figure {\PageIndex{2}} mostra uma massa m ligada a uma mola com uma constante de força k. A massa é elevada a uma posição A0, a amplitude inicial, e depois libertada. A massa oscila em torno da posição de equilíbrio num fluido com viscosidade, mas a amplitude diminui a cada oscilação. Para um sistema que tem uma pequena quantidade de amortecimento, o período e frequência são constantes e são quase os mesmos que para SHM, mas a amplitude diminui gradualmente como mostrado. Isto ocorre porque a força de amortecimento não conservadora remove energia do sistema, geralmente sob a forma de energia térmica.

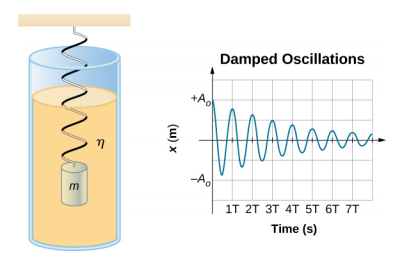
Considerar as forças que actuam sobre a massa. Note-se que a única contribuição do peso é a alteração da posição de equilíbrio, como discutido anteriormente no capítulo. Portanto, a força líquida é igual à força da mola e à força de amortecimento (F_D\)). Se a magnitude da velocidade é pequena, significando que a massa oscila lentamente, a força de amortecimento é proporcional à velocidade e actua contra a direcção do movimento (\(F_D = -b\)). A força líquida sobre a massa é, portanto,

p>>p> Escrevendo isto como uma equação diferencial em x, obtemos

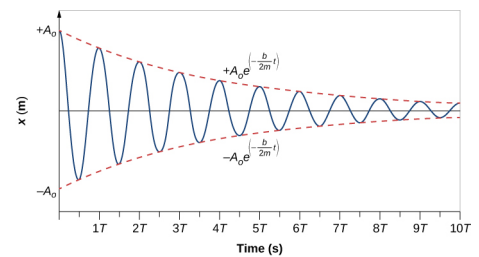
>p>>p> Para determinar a solução para esta equação, considerar o gráfico de posição versus tempo mostrado na Figura \(\PageIndex{3}). A curva assemelha-se a uma curva cosina oscilando no envelope de uma função exponencial (A_0e^{-alpha t}) onde {(|alpha = |frac{b}{2m}). A solução é

>p> É deixado como um exercício para provar que esta é, de facto, a solução. Para provar que é a solução certa, tomar a primeira e a segunda derivadas em relação ao tempo e substituí-las na Equação 15.23. Descobre-se que a Equação 15.24 é a solução se

\

Recordar que a frequência angular de uma massa submetida a SHM é igual à raiz quadrada da constante de força dividida pela massa. Isto é frequentemente referido como a frequência angular natural, que é representada como

\

A frequência angular para o movimento harmónico amortecido torna-se

\

Recordar que quando começámos esta descrição do movimento harmónico amortecido, afirmámos que o amortecimento deve ser pequeno. Duas perguntas nos vêm à mente. Porque é que o amortecimento tem de ser pequeno? E quão pequeno é pequeno? Se se aumentar gradualmente a quantidade de amortecimento num sistema, o período e a frequência começam a ser afectados, porque o amortecimento se opõe e, portanto, retarda o movimento de ida e volta. (A força da rede é menor em ambos os sentidos). Se houver um amortecimento muito grande, o sistema nem sequer oscilar – move-se lentamente em direcção ao equilíbrio. A frequência angular é igual a

p>>p>Como b aumenta, ^(m) – esquerda(b) – direita(2m) – esquerda(b) – direita(2m)) torna-se menor e eventualmente atinge zero quando b = b = 4mk). Se b se tornar maior, b = b = frac = k = – esquerda = b = frac = b = direita = 2m) torna-se um número negativo e b =qrt = frac = k = – esquerda = b = frac = b = direita = 2m) é um número complexo.

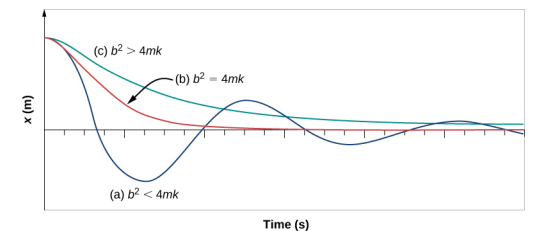
Figure {4}} mostra o deslocamento de um oscilador harmónico para diferentes quantidades de amortecimento.

1. Quando a constante de amortecimento é pequena, b < \\(\sqrt{4mk}}), o sistema oscila enquanto a amplitude do movimento decai exponencialmente. Diz-se que este sistema está subamortecido, como na curva (a). Muitos sistemas estão subamortecidos, e oscilam enquanto a amplitude diminui exponencialmente, tal como a massa oscila numa mola. O amortecimento pode ser bastante pequeno, mas eventualmente a massa vem em repouso.
2. Se a constante de amortecimento for \(b = \sqrt{4mk}}), diz-se que o sistema está gravemente amortecido, como em curva (b)). Um exemplo de um sistema gravemente humedecido são os amortecedores de choque num carro. É vantajoso que as oscilações se decomponham o mais rápido possível. Aqui, o sistema não oscila, mas aproxima-se assimmptoticamente da condição de equilíbrio o mais rapidamente possível.

li>Curve (c) na Figura \PageIndex{4}} representa um sistema sobre-humidificado onde { b >sqrt{4mk}). Um sistema sobrealimentado aproximar-se-á do equilíbrio durante um período de tempo mais longo.

O amortecimento crítico é frequentemente desejado, porque tal sistema regressa rapidamente ao equilíbrio e permanece também em equilíbrio. Além disso, uma força constante aplicada a um sistema gravemente amortecido move o sistema para uma nova posição de equilíbrio no menor tempo possível sem ultrapassar ou oscilar sobre a nova posição.