قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).
Definition
A lei de Bragg fornece a condição para uma onda plana ser difratada por uma família de planos de treliça:
2 d sin θ = n λ
onde d é o espaçamento interplanar, θ o ângulo entre o vector de onda da onda plana incidente, ko, e os planos da malha, λ o seu comprimento de onda e n é um inteiro, a ordem da reflexão. É equivalente à condição de difracção no espaço recíproco e às equações de Laue.
Derivação directa da lei de Bragg
- Reflexão do primeiro plano
As ondas dispersas estarão em fase qualquer que seja a distribuição dos dispersores de pontos no primeiro plano se o ângulo do vector de onda reflectido, kh, for também igual a θ. Esta é a lei de reflexão de Snell-Descartes.
- Reflexão do segundo plano
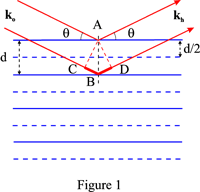
Desde que a fase das ondas reflectidas é independente da posição do dispersor de pontos no plano, a diferença de fase entre as ondas reflectidas por dois planos de grelha sucessivos é obtida escolhendo arbitrariamente um ponto de dispersão, A, no primeiro plano e um ponto de dispersão, B, no segundo plano, de modo a que AB seja normal para os planos. Se C e D são as projecções de A sobre os vectores de onda incidentes e reflectidos que passam por B, a Figura 1 mostra claramente que a diferença de percurso entre as ondas reflectidas em A e B, respectivamente, é:
CB + BD = 2d sin θ
e que as duas ondas estarão em fase se esta diferença de caminho for igual a nλ onde n é um número inteiro.
- Reflexão do terceiro, etc. planos
Se a relação de Bragg estiver satisfeita para os dois primeiros planos, as ondas reflectidas com o vector de onda kh estarão em fase para todos os planos da família.
Ordem da reflexão
A lei de Bragg também pode ser escrita:
2 (d/n) sin θ = λ.
Pode-se então dizer que um Bragg reflexão de ordem n numa família de planos de grelha de ordem n é equivalente à reflexão de ordem 1 numa família de planos de grelha de espaçamento fictício, ou imaginário
d_{hkl} = d/n.
Esta família fictícia está associada ao vector de malha recíproca OH onde OH = n/d = 1/d_{hkl}. Os índices da reflexão são hkl. Por exemplo, as linhas horizontais tracejadas na Figura 1 correspondem aos planos fictícios associados à segunda ordem, n = 2.
Condições de reflexão
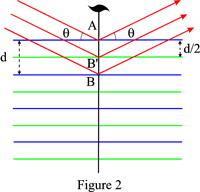
Se houver um plano de planeio ou um eixo de parafuso normal para os planos de grelha, o espaçamento dos planos reflectores reais é d/2 para um plano de planeio e (d p/q) para um eixo de parafuso qp. A lei de Bragg deve então ser escrita:
2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ
para um plano de planeio e
2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ
para um eixo de parafuso qp.
Os reflexos de ordem ímpar para um plano de planeio e de ordem diferente de (q/p)n para um eixo de parafuso estão então ausentes. Fala-se de ausências sistemáticas relacionadas com a presença de componentes de planeio ou parafuso.
Como exemplo, a Figura 2 mostra o caso de um eixo de 21 parafusos: os planos reflectores são os planos azuis e os planos verdes deduzidos destes últimos pela acção do eixo do parafuso. Reflexões de ordem estranha estarão sistematicamente ausentes.
Influência da deformação
Uma deformação que deixa uma família de planos de malha (hkl) sem distorções e o seu espaçamento de malha d inalterado não afectará o ângulo de Bragg dos reflexos kkl, e.g. planos de grelha paralelos a um deslocamento de parafuso.
História
Bragg (1890-1971) apresentou a sua derivação da condição de reflexão numa reunião da Sociedade Filosófica de Cambridge a 11 de Novembro de 1912. O seu trabalho foi publicado em 1913. Para detalhes, ver P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Secção 5, p. 64 e A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Secção 6.11, p. 120.
See também
- equações de Laue