Introduction

Column Buckling é um assunto curioso e único. É talvez a única área da mecânica estrutural em que a falha não está relacionada com a resistência do material. Uma análise de encurvadura de coluna consiste em determinar a carga máxima que uma coluna pode suportar antes de colapsar. Mas para colunas longas, o colapso não tem nada a ver com o rendimento do material. É governada pela rigidez da coluna, tanto material como geométrica.
Esta página irá derivar as equações padrão da encurvadura da coluna utilizando duas abordagens. Em primeiro lugar, irá cobrir o desenvolvimento habitual das equações, ou seja, a Teoria da Encurvadura de Euler. Esta é a derivação encontrada em livros de texto e apresentada em cursos de engenharia. Mas nunca gostei dela. Não porque seja incorrecta (é correcta), mas porque não creio que apresente satisfatoriamente os mecanismos físicos que regem o processo de encurvadura. É por isso que uma segunda derivação das equações de encurvadura também será apresentada.
Curiamente, os objectos são referidos como colunas quando são carregados axialmente em compressão, como é o caso aqui, mas são referidos como vigas quando são carregados transversalmente.No entanto, a teoria da flexão de vigas é central nas análises de encurvadura de colunas, pelo que se recomenda que o leitor reveja esta página de flexão de vigas.

Teoria de Buckling Euler

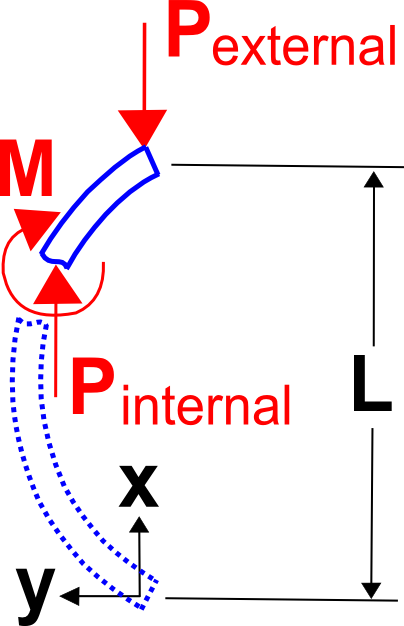
Teoria de Buckling Euler é a teoria clássica apresentada em livros escolares e salas de aula. Começa simplesmente por observar que o momento de flexão interna numa coluna carregada e deformada é a carga compressiva e a columeflexão. Por isso, inserir { -P, y” = M } na equação de flexão do feixe, { E, I, y” = M }. sto produz a seguinte equação diferencial
br>br>br> que tem a solução
br>br>br>onde A(A) e B(B) são constantes determinadas a partir das condições de contorno.
As condições de limite são \\(y = 0\) a \(x = 0\) e \(x = L\).
A primeira condição de limite, \(y = 0\) a \(x = 0\), leva a concluir que \(B = 0\). E isto deixa
br>br> tão bom, tão bom. Mas é neste ponto que a derivação clássica tende a deixar para trás a intuição física e a tornar-se abertamente matemática…
As coisas tornam-se muito interessantes com a segunda condição limite porque, como veremos, não leva à determinação do incognoscível, {\an8}(A). Para ver isto, inserir a segunda condição de limite como se segue.
br>Existem basicamente duas possibilidades aqui. No primeiro caso, {A = 0}, mas isto é aborrecido porque leva ao resultado de que todas as colocações são zero. Esta é apenas a solução sem fivelas. Antes das fivelas da coluna, os seus deslocamentos laterais são simplesmente zero.

O segundo caso é o interessante, e o directamente relacionado com a fivela da coluna. O segundo método para satisfazer a condição de contorno é notar que {sin(\pi) = 0\pi}. Portanto, a forma de satisfazer a condição de contorno é exigir que o argumento na equação,esquerda( Pqrt{P sobre E, I; L direita)}) seja igual a 0.Fazendo-o dá

{\i}br> e resolvendo para {\i}br>>br>>br>>br> Este é o resultado clássico da teoria da encurvadura de Euler. Dá o valor crítico da carga, chamado P_{cr}, acima do qual, a coluna se afivelará. ste resultado é perfeitamente legítimo. No entanto, como já deveria ser evidente, é de natureza muito matemática, e proporciona pouca percepção física como resultado. A derivação ascendente abaixo apresentará um método analitivo para chegar à mesma equação que, creio, proporciona uma ligação física muito mais directa ao processo de encurvadura que a derivação acima fez.

Buckling vs Yielding

Como foi dito no início, a análise clássica da encurvadura é independente da força de rendimento de um material. Isto é evidente na derivação acima referida porque em nenhum momento foi discutida a tensão ou tensão em comparação com a resistência de um material.
Mas, de facto, as considerações de cedência nunca devem ser totalmente ignoradas. Assim que se obtém uma estimativa de P_cr da equação acima, deve-se sempre dividi-la pela área da secção transversal da coluna,{(A), para obter uma tensão
br>br> e comparar este valor com a resistência de cedência do material para determinar se a cedência ocorrerá antes da deformação. Isto é crítico para as colunas curtas, pois têm valores intrinsecamente elevados,porque L^2 está no denominador da sequência de encurvadura.

End Constraints in Buckling

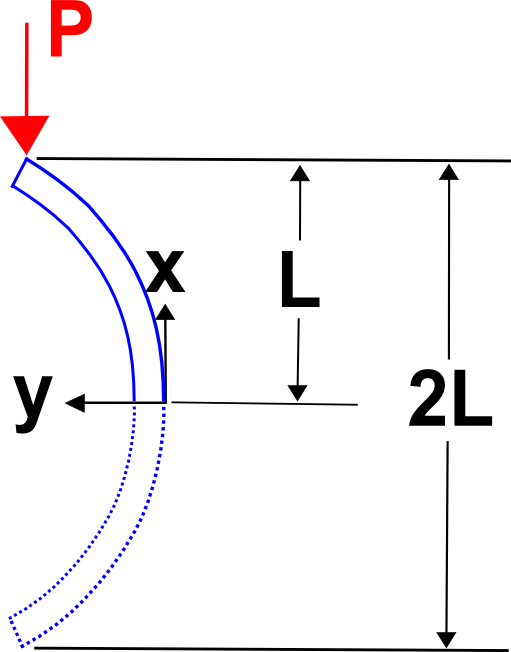
embora não seja o foco desta página, é importante reconhecer que os constrangimentos finais são críticos para as análises de encurvadura porque alteram o valor de {cr}}(P_{cr}}). Por exemplo,considere que a carga crítica de encurvadura da coluna aqui mostrada é dada por
br>Note que este valor é 1/4 do valor dado na equação anterior para {(P_{cr}}),mas é fácil de ver porquê. O esboço mostra que a condição de encurvadura aqui mostrada é exactamente equivalente à encurvadura de uma coluna com o dobro do comprimento e com as mesmas condições de contorno que na derivação acima referida. E isto leva a
/div>

Derivação de encurvadura com base física

Esta secção apresentará um método alternativo de determinação de cargas críticas de encurvadura que acredito ser mais intuitivo fisicamente do que a clássica teoria de encurvadura de Euler. A sua característica chave é a comparação do momento de flexão interno resultante da distribuição de tensão interna ao momento de flexão externo resultante da carga aplicada à coluna. (A frase anterior é crítica.)
Esta abordagem retoma aproximadamente onde anteriormente se notou que a abordagem clássica de Euler se torna abertamente matemática. O primeiro passo consiste em assumir uma forma deformada. Sabemos que \(y = 0\) em ambas as extremidades da coluna, e que a forma segue uma função \(\sin()\) baseada na equação acima referida. Assim, a escolha mais lógica é
br> onde {delta_{max}} é o deslocamento lateral no ponto médio da coluna. O seu valor é desconhecido, mas sabe-se que é maior no ponto médio do que em qualquer outro ponto da coluna, daí o subscrito {max}. A escolha da função {\pi x / L} como argumento da função {\sin()}) assegura que os deslocamentos são zero em {\ x = 0} e {\ x = L}. (Falaremos brevemente sobre outras formas assumidas.)

Se estiver a pensar sobre o termo \sqrt{P/EI} na função \sin()} da solução anterior de Euler, não o faça. Surgiu da solução da equação diferencial, mas estamos a fingir não saber nada sobre os detalhes dessa solução aqui (alerta de excepção!). Só precisamos de uma função que possa assemelhar-se a uma coluna arqueada com deslocamentos zero nas suas extremidades. O “alerta de excepção” está presente acima porque estamos de facto a tirar partido de um pedaço de conhecimento sobre a análise anterior. É que as funções trigonométricas são as soluções da equação diferencial. Por conseguinte, os pecados e os cossenos devem ser utilizados sempre que possível para descrever as formas deformadas, porque elas conduzirão às estimativas mais precisas de {\i}(P_{cr}}).

Recordar da teoria da flexão de viga que o momento de flexão, (M), está relacionado com a deflexão da coluna por
br>br>>br> Não sendo crítico, é útil recordar que esta relação se deveu ao cálculo do momento na secção transversal devido à distribuição da tensão. A relação mostra que precisamos do segundo derivado da suposta função de deslocamento.

\\\\\br> Este é o momento de flexão interna da coluna devido à distribuição de tensão dentro dela, que por sua vez se deve ao facto de a coluna estar dobrada.
Aqui vem um pensamento importante… Este momento de flexão pode ser pensado na resistência interna da coluna à flexão, ou na força com que tenta endireitar-se para fora.
A próxima etapa é simplesmente equacionar este momento de flexão resistivo interno com o resultante da carga externa. Essa quantidade é simplesmente\\(M = -P \, y(x)\). Equacionando os dois dá
br> Não é difícil ver neste momento que esta abordagem está a conduzir à mesma expressão para { P_{cr}} como a clássica teoria da encurvadura de Euler. Mas ao longo do caminho, tem proporcionado muito mais visão do processo físico da encurvadura do que a teoria anterior. Nomeadamente…

/ol>Anyway, anulando \(y(x)\) de ambos os lados da equação dá
br>br>again, mas com muito mais discernimento físico desta vez.

Fixed End Example

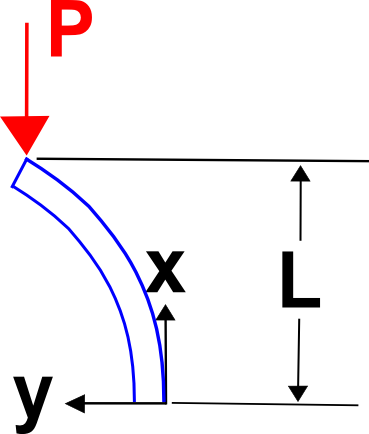
/div> Desta vez, assumir uma forma deformada de
br>br>Calcular o momento de flexão devido a isto. momento de flexão devido à carga externa é { M = P ( \delta_{max}) – y(x) )\). Equilibrar estes dois e simplificar dá o resultado familiar.
\

Exemplo Final Fixo com Forma Assumida Diferente

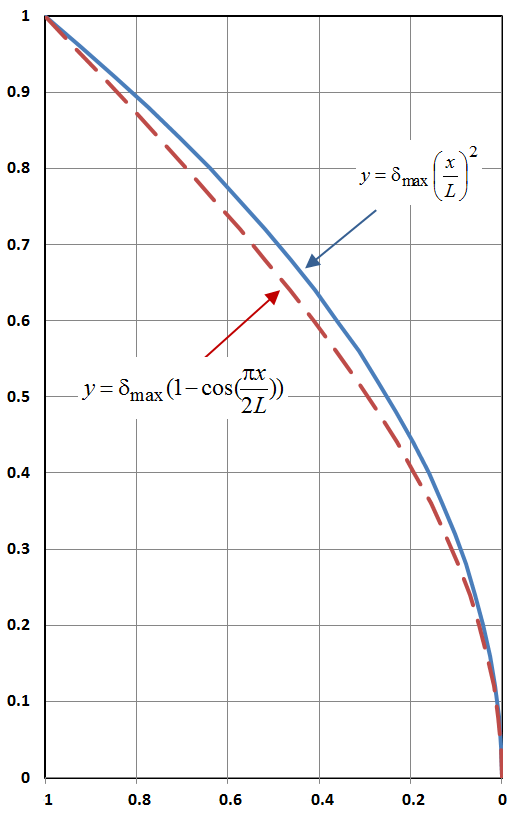
Este exemplo demonstrará que funções alternativas podem ser assumidas para a forma deformada da coluna, e que a fórmula resultante para {cr}(P_{cr}) não será significativamente diferente da solução exacta.
Esta vez, assumir uma forma deformada de
br>br>Calcular o momento de flexão devido a isto.
br>br>br> O momento de flexão devido à carga externa permanece \(M = P ( {delta_{max} – y(x) )\). Equacionando estes dois dá
br>br> É claro a partir da equação que o valor mínimo de {(P) ocorrerá em {x = 0}) porque é neste ponto que {y(x)} é um mínimo (zero, de facto) e portanto((delta_{max}) – y(x))\) é um máximo. A definição de {y(x)}(y(x)}) a zero e o cancelamento de {delta_{max}) de ambos os lados dá

Este resultado não é obviamente igual à solução exacta acima referida. A diferença é que a solução exacta contém {\pi^2 / 4 = 2,467}, enquanto que esta solução aproximada contém 2,a 23% de diferença. Significativa, mas não grande como, digamos, um factor de 2, ou uma ordem de grandeza. Note-se também que a solução aproximada é conservadora, uma vez que dá uma encurvadura crítica sem carga do que a da solução exacta.
É interessante notar que esta solução baseada na forma quadrática, levou a uma menor carga crítica de encurvadura e a uma concentração da falha de encurvadura na base da coluna, \(x = 0\).Em contraste, a solução exacta que consiste na função trigonométrica, produziu uma tendência de encurvadura igual ao longo de todo o comprimento da coluna, e uma correspondente maior \(P_{cr}}).
Um factor chave aqui é que a forma quadrática deformada assumida não é uma solução exacta da equação diferencial governante (embora esteja próxima). As funções Trig são.