Última actualização em 25 de Setembro de 2019
Em vez de prever valores de classe directamente para um problema de classificação, pode ser conveniente prever a probabilidade de uma observação pertencente a cada classe possível.
Prever probabilidades permite alguma flexibilidade, incluindo decidir como interpretar as probabilidades, apresentando previsões com incerteza, e fornecendo formas mais nuances para avaliar a capacidade do modelo.
Probabilidades previstas que correspondem à distribuição esperada de probabilidades para cada classe são referidas como calibradas. O problema é que nem todos os modelos de aprendizagem de máquinas são capazes de prever probabilidades calibradas.
Existem métodos tanto para diagnosticar como são calibradas as probabilidades previstas e para melhor calibrar as probabilidades previstas com a distribuição observada de cada classe. Muitas vezes, isto pode levar a previsões de melhor qualidade, dependendo de como a capacidade do modelo é avaliada.
Neste tutorial, descobrirá a importância de calibrar as probabilidades previstas e como diagnosticar e melhorar a calibração dos modelos utilizados para a classificação probabilística.
Após completar este tutorial, saberá:
- algoritmos de aprendizagem não-linear de máquinas prevêem frequentemente probabilidades de classe não calibradas.
- diagramas de fiabilidade podem ser usados para diagnosticar a calibração de um modelo, e os métodos podem ser usados para melhor calibrar as previsões para um problema.
- Como desenvolver diagramas de fiabilidade e calibrar modelos de classificação em Python com scikit-learn.
P>Dê início ao seu projecto com o meu novo livro Probability for Machine Learning, incluindo tutoriais passo-a-passo e os ficheiros de código fonte Python para todos os exemplos.
P>Damos início.

Como e Quando Utilizar um Modelo de Classificação Calibrado com scikit-learn
Photo de Nigel Howe, alguns direitos reservados.
Síntese tutorial
Este tutorial está dividido em quatro partes; são elas
- Probabilidades de Previsão
- Calibração de Previsões
- Como calibrar probabilidades em Python
- Exemplo trabalhado de calibração de probabilidades de SVM
Probabilidades de Previsão
Um problema de modelação preditiva de classificação requer a previsão ou previsão de uma etiqueta para uma determinada observação.
Uma alternativa à previsão directa da etiqueta, um modelo pode prever a probabilidade de uma observação pertencente a cada etiqueta de classe possível.
Isto proporciona alguma flexibilidade tanto na forma como as previsões são interpretadas e apresentadas (escolha do limiar e incerteza da previsão) como na forma como o modelo é avaliado.
Embora um modelo possa ser capaz de prever probabilidades, a distribuição e comportamento das probabilidades pode não corresponder à distribuição esperada das probabilidades observadas nos dados de formação.
Isto é especialmente comum com algoritmos complexos de aprendizagem não-linear de máquinas que não fazem directamente previsões probabilísticas e utilizam aproximações.
A distribuição das probabilidades pode ser ajustada para melhor corresponder à distribuição esperada observada nos dados. Este ajustamento é referido como calibração, como na calibração do modelo ou na calibração da distribuição das probabilidades de classe.
desejamos que as probabilidades de classe estimadas sejam o reflexo da verdadeira probabilidade subjacente da amostra. Ou seja, a probabilidade de classe prevista (ou o valor de probabilidades) precisa de ser bem calibrada. Para serem bem calibradas, as probabilidades devem reflectir efectivamente a verdadeira probabilidade do evento de interesse.
– Página 249, Applied Predictive Modeling, 2013.
Calibration of Predictions
Existem duas preocupações na calibração das probabilidades; elas estão a diagnosticar a calibração das probabilidades previstas e o próprio processo de calibração.
Diagramas de Fiabilidade (Curvas de Calibração)
Um diagrama de fiabilidade é um gráfico da frequência relativa do que foi observado (eixo y) versus a frequência de probabilidade prevista (eixo x).
Diagramas de fiabilidade são ajudas comuns para ilustrar as propriedades dos sistemas de previsão probabilística. Consistem num gráfico da frequência relativa observada contra a probabilidade prevista, fornecendo uma rápida intercomparação visual ao afinar os sistemas de previsão probabilística, bem como documentando o desempenho do produto final
– Aumentando a Fiabilidade dos Diagramas de Fiabilidade, 2007.
Especificamente, as probabilidades previstas são divididas num número fixo de baldes ao longo do eixo x. O número de eventos (classe=1) é então contado para cada balde (por exemplo, a frequência relativa observada). Finalmente, as contagens são normalizadas. Os resultados são então traçados como um gráfico de linha.
Estes gráficos são geralmente referidos como diagramas de ‘fiabilidade’ na literatura de previsão, embora também possam ser chamados de gráficos ou curvas de ‘calibração’, uma vez que resumem a forma como as probabilidades de previsão são calibradas.
Quanto melhor calibrada ou mais fiável for uma previsão, mais perto os pontos aparecerão ao longo da diagonal principal desde a parte inferior esquerda até à parte superior direita do gráfico.
A posição dos pontos ou a curva relativa à diagonal pode ajudar a interpretar as probabilidades; por exemplo:
- Abaixo da diagonal: O modelo tem uma previsão excessiva; as probabilidades são demasiado grandes.
- Acima da diagonal: O modelo tem sub-previsão; as probabilidades são demasiado pequenas.
Probabilidades, por definição, são contínuas, pelo que esperamos alguma separação da linha, muitas vezes mostrada como uma curva em forma de S mostrando tendências pessimistas sobre-previsão de probabilidades baixas e sub-previsão de probabilidades altas.
Diagramas de fiabilidade fornecem um diagnóstico para verificar se o valor de previsão Xi é fiável. Grosso modo, uma previsão de probabilidade é fiável se o evento acontecer realmente com uma frequência relativa observada consistente com o valor da previsão.
– Aumentando a Fiabilidade dos Diagramas de Fiabilidade, 2007.
O diagrama de fiabilidade pode ajudar a compreender a calibração relativa das previsões de diferentes modelos preditivos.
Quer aprender Probabilidade de Aprendizagem de Máquina
Fazer agora o meu curso intensivo de 7 dias por correio electrónico gratuito (com código de amostra).
Clique para se inscrever e também obter uma versão PDF Ebook gratuita do curso.
p>Download Your FREE Mini-Course
Calibração de Probabilidade
As previsões feitas por um modelo preditivo podem ser calibradas.
Previsões calibradas podem (ou não) resultar numa calibração melhorada num diagrama de fiabilidade.
Alguns algoritmos são adequados de tal forma que as suas probabilidades previstas já estão calibradas. Sem entrar em detalhes do porquê, a regressão logística é um desses exemplos.
Outros algoritmos não produzem directamente previsões de probabilidades, e em vez disso uma previsão de probabilidades deve ser aproximada. Alguns exemplos incluem redes neurais, máquinas vectoriais de suporte, e árvores de decisão.
As probabilidades previstas a partir destes métodos provavelmente não serão calibradas e poderão beneficiar de ser modificadas via calibração.
Calibração das probabilidades de previsão é uma operação de redimensionamento que é aplicada após as previsões terem sido feitas por um modelo preditivo.
Existem duas abordagens populares para calibrar probabilidades; são a Escala Platt e a Regressão Isotónica.
A Escala Platt é mais simples e é adequada para diagramas de fiabilidade com a forma S. A Regressão Isotónica é mais complexa, requer muito mais dados (caso contrário pode sobreajustar-se), mas pode suportar diagramas de fiabilidade com diferentes formas (não é paramétrica).
Platt Scaling é mais eficaz quando a distorção nas probabilidades previstas tem a forma sigmóide. A Regressão Isotónica é um método de calibração mais potente que pode corrigir qualquer distorção monotónica. Infelizmente, esta potência extra vem a um preço. Uma análise da curva de aprendizagem mostra que a Regressão Isotónica é mais propensa a sobreajustamento, e assim tem um desempenho pior do que o Platt Scaling, quando os dados são escassos.
– Prevendo Boas Probabilidades com Aprendizagem Supervisionada, 2005.
Nota, e isto é realmente importante: probabilidades melhor calibradas podem ou não conduzir a melhores previsões baseadas na classe ou em probabilidades. Depende realmente da métrica específica utilizada para avaliar as previsões.
De facto, alguns resultados empíricos sugerem que os algoritmos que podem beneficiar mais da calibração das probabilidades previstas incluem SVMs, árvores de decisão ensacadas, e florestas aleatórias.
após a calibração, os melhores métodos são árvores, florestas aleatórias e SVMs.
– Predicting Good Probabilities With Supervised Learning, 2005.
Como calibrar probabilidades em Python
A biblioteca de aprendizagem de máquinas de aprendizagem scikit-learn permite tanto diagnosticar a calibração de probabilidades de um classificador como calibrar um classificador que possa prever probabilidades.
Diagnosticar Calibração
É possível diagnosticar a calibração de um classificador criando um diagrama de fiabilidade das probabilidades reais versus as probabilidades previstas num conjunto de testes.
Em scikit-learn, isto chama-se uma curva de calibração.
Isto pode ser implementado calculando primeiro a função calibration_curve(). Esta função toma os verdadeiros valores de classe para um conjunto de dados e as probabilidades previstas para a classe principal (class=1). A função retorna as probabilidades reais para cada contentor e as probabilidades previstas para cada contentor. O número de caixas pode ser especificado através do argumento de n_bins e por defeito para 5.
Por exemplo, abaixo está um snippet de código mostrando a utilização da API:
|
1
2
3
4
5
6
7
8
9
10
|
Calibrate Classifier
Um classificador pode ser calibrado em scikit-learn utilizando a classe CalibratedClassifierCV.
Existem duas formas de utilizar esta classe: pré-instalação e validação cruzada.
P>Pode caber um modelo num conjunto de dados de formação e calibrar este modelo de pré-validação usando um conjunto de dados de validação hold out.
Por exemplo, abaixo está um trecho de código que mostra a utilização da API:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
Alternately, o CalibratedClassifierCV pode caber várias cópias do modelo utilizando a validação cruzada k-fold e calibrar as probabilidades previstas por estes modelos utilizando o hold out set. As previsões são feitas utilizando cada um dos modelos treinados.
Por exemplo, abaixo está um trecho de código que mostra a utilização do API:
|
1
2
3
4
5
6
7
8
9
10
11
|
/div>
A classe CalibratedClassifierCV suporta dois tipos de calibração de probabilidade; especificamente, o método paramétrico ‘sigmoid’ (método de Platt) e o método não paramétrico ‘isotónico’ que pode ser especificado através do argumento ‘método’.
Exemplo trabalhado de calibração das probabilidades de SVM
Podemos concretizar a discussão da calibração com alguns exemplos trabalhados.
Nestes exemplos, vamos ajustar uma máquina vectorial de suporte (SVM) a um problema ruidoso de classificação binária e usar o modelo para prever probabilidades, depois rever a calibração usando um diagrama de fiabilidade e calibrar o classificador e rever o resultado.
SVM é um bom modelo candidato para calibrar porque não prevê nativamente as probabilidades, o que significa que as probabilidades são frequentemente não calibradas.
Uma nota sobre SVM: as probabilidades podem ser previstas chamando a função decision_function() ao modelo de ajuste em vez da função habitual predict_proba(). As probabilidades não são normalizadas, mas podem ser normalizadas quando se chama a função calibration_curve() definindo o argumento ‘normalize’ para ‘True’.
O exemplo abaixo encaixa um modelo SVM no problema do teste, prevê probabilidades, e traça a calibração das probabilidades como um diagrama de fiabilidade,
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
>/td> # Diagrama de fiabilidade SVM
do sklearn.importação de conjuntos de dados make_classification
de sklearn.svm importação SVC
de sklearn.model_selection importação de train_test_split
de sklearn.calibration import calibration_curve
from matplotlib import pyplot
# generate 2 class dataet
X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1)
# dividido em conjuntos comboio/teste
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# caber um modelo
modelo = SVC()
model.fit(trainX, trainy)
# prever probabilidades
probs = modelo.decision_function(testX)
# diagrama de fiabilidade
fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True)
# plot perfeitamente calibrado
pyplot.plot(, , linestyle=’–‘)
# fiabilidade do modelo de plot
pyplot.plot(mpv, fop, marker=’.’)
pyplot.show()
|
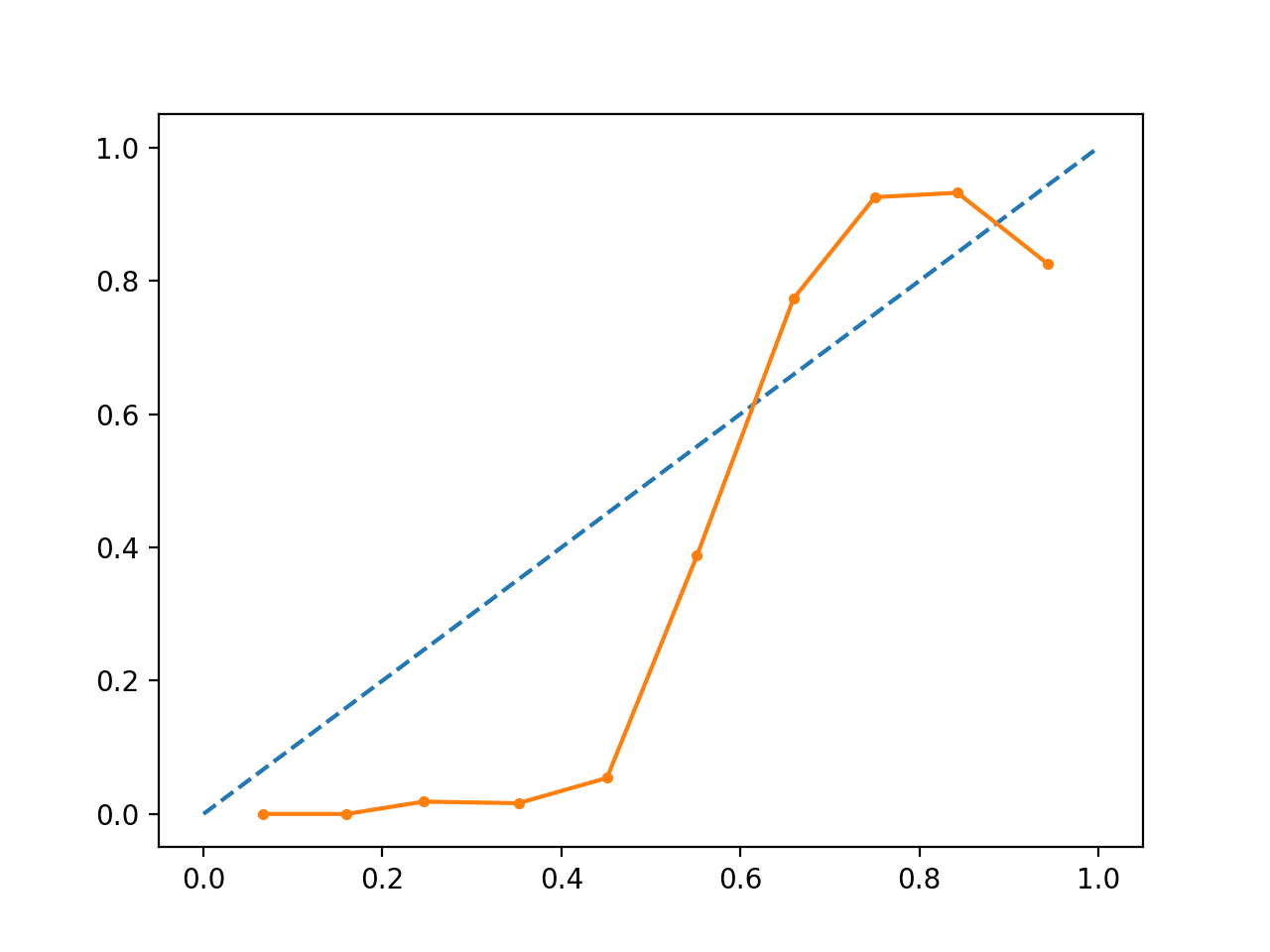
Executar o exemplo cria um diagrama de fiabilidade mostrando a calibração das probabilidades previstas das SVMs (linha sólida) em comparação com um modelo perfeitamente calibrado ao longo da diagonal da parcela (linha tracejada.)
Vemos a curva em forma de S esperada de uma previsão conservadora.
 p>Diagrama de Fiabilidade SVM não calibrado
p>Diagrama de Fiabilidade SVM não calibrado P>Podemos actualizar o exemplo para ajustar a SVM através da classe CalibratedClassifierCV usando a validação cruzada de 5 vezes, usando os conjuntos de holdout para calibrar as probabilidades previstas.
O exemplo completo é listado abaixo.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/td> # diagrama de fiabilidade SVM com calibração
a partir do sklearn.importação de conjuntos de dados make_classification
de sklearn.svm importação SVC
de sklearn.calibration importação de CalibratedClassifierCV
de sklearn.model_selection importação de train_test_split
de sklearn.calibration import calibration_curve
from matplotlib import pyplot
# generate 2 class dataet
X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1)
# dividido em conjuntos comboio/teste
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# caber um modelo
modelo = SVC()
calibrado = CalibratedClassifierCV(model, method=’sigmoid’, cv=5)
calibrado.fit(trainX, trainy)
# predict probabilities
probs = calibrado.predict_proba(testX)
# diagrama de fiabilidade
fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True)
# plot perfeitamente calibrado
pyplot.plot(, , linestyle=’–‘)
# plot fiabilidade calibrada
pyplot.plot(mpv, fop, marker=’.’)
pyplot.show()
|
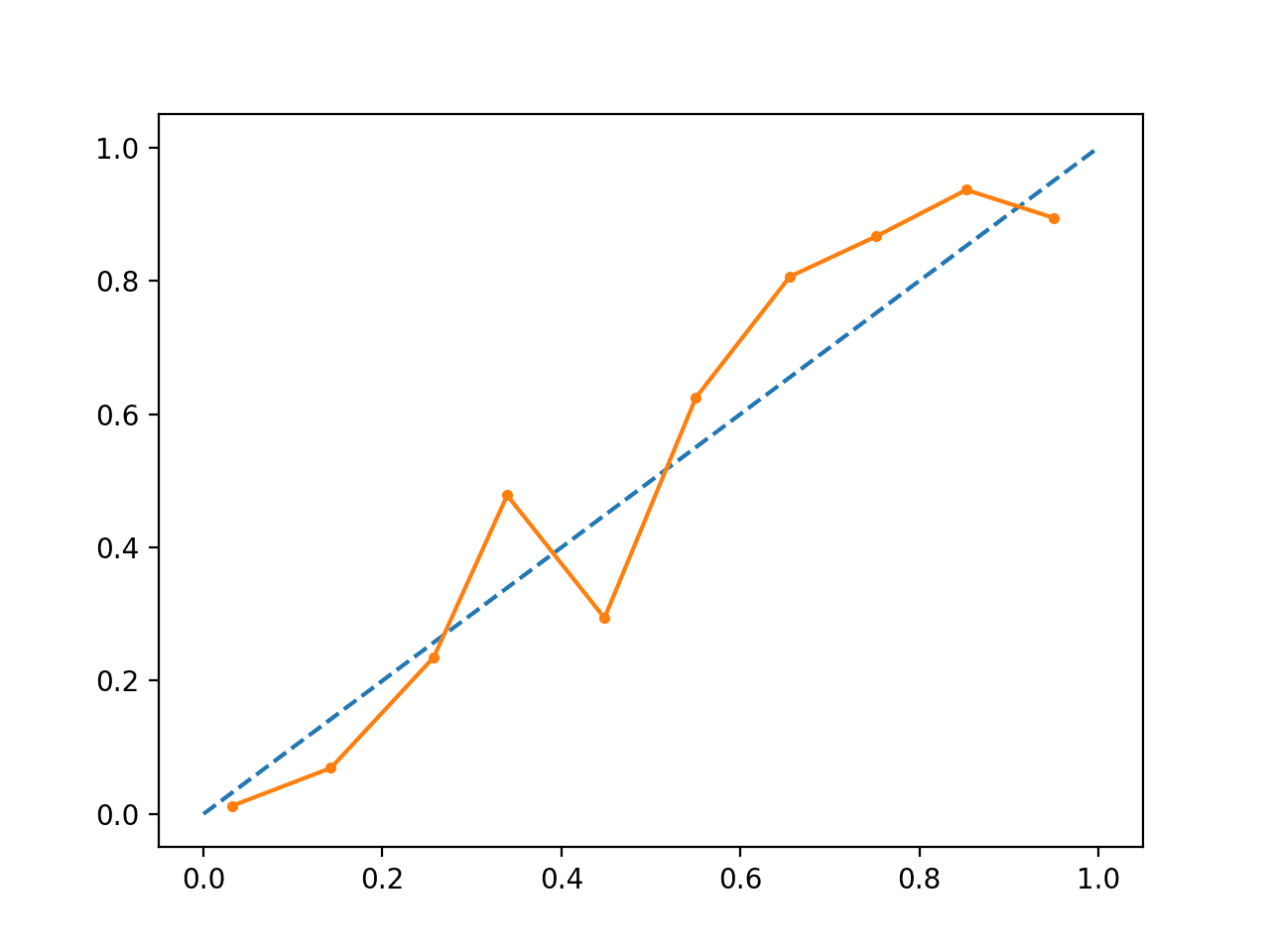
Executar o exemplo cria um diagrama de fiabilidade para as probabilidades calibradas.
A forma das probabilidades calibradas é diferente, abraçando a linha diagonal muito melhor, embora ainda com pouca previsão no quadrante superior.
Visualmente, o gráfico sugere um modelo melhor calibrado.
 p>Diagrama de Fiabilidade SVM Calibrado
p>Diagrama de Fiabilidade SVM Calibrado Podemos tornar o contraste entre os dois modelos mais óbvio, incluindo ambos os diagramas de fiabilidade no mesmo gráfico.
O exemplo completo está listado abaixo.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
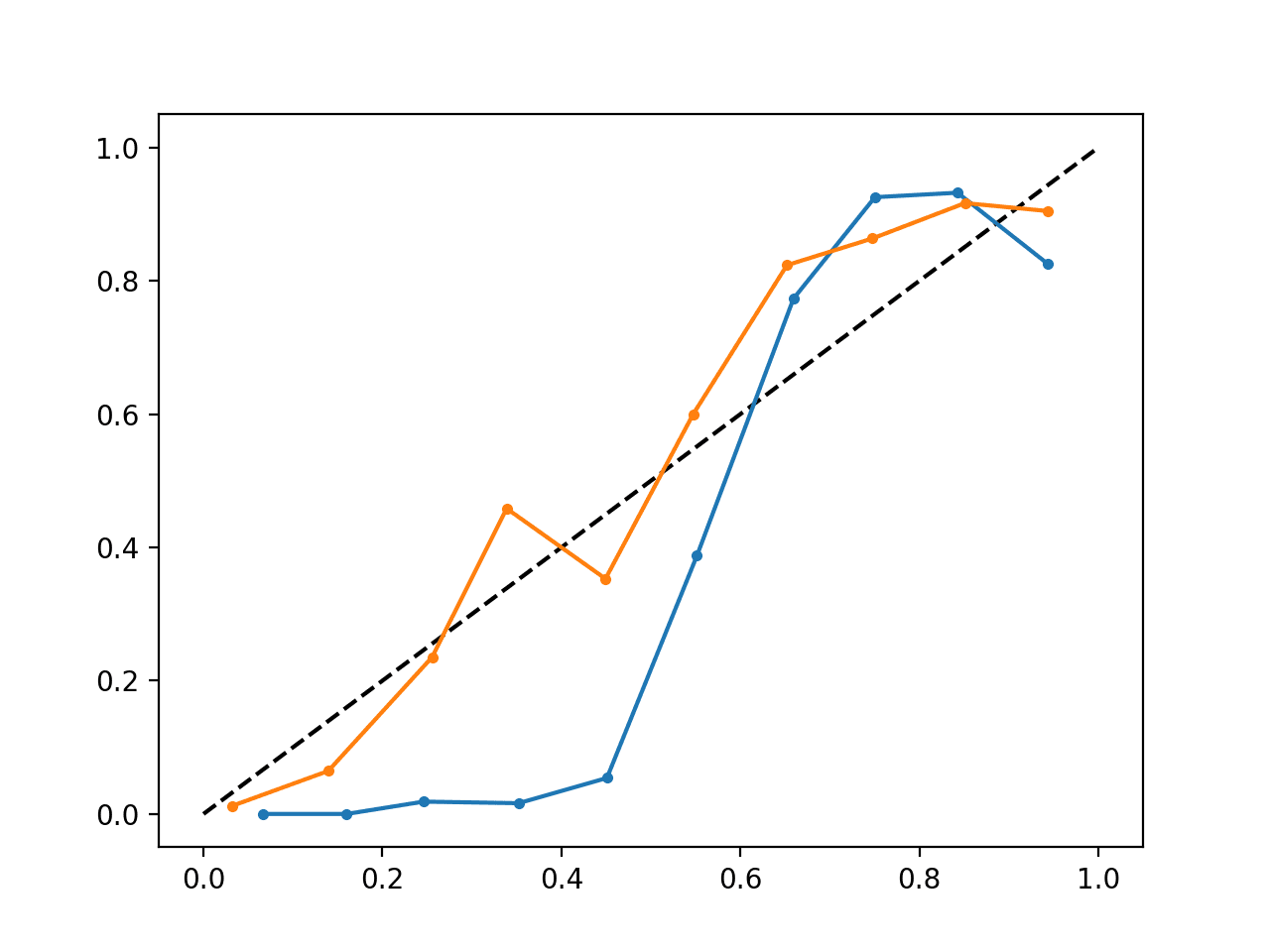
Executar o exemplo cria um único diagrama de fiabilidade mostrando tanto as probabilidades calibradas (laranja) como não calibradas (azul).
Não é realmente uma comparação maçãs-maçãs, uma vez que as previsões feitas pelo modelo calibrado são de facto uma combinação de cinco submodelos.
Não obstante, vemos uma diferença acentuada na fiabilidade das probabilidades calibradas (muito provavelmente causada pelo processo de calibração).
 p>Diagrama de Fiabilidade SVM calibrado e não calibrado
p>Diagrama de Fiabilidade SVM calibrado e não calibrado Outras Leituras
Esta secção fornece mais recursos sobre o tópico, se pretender ir mais fundo.
Livros e Documentos
- Modelação Preditiva Aplicada, 2013.
- Predicting Good Probabilities With Supervised Learning, 2005.
- Obtenção de estimativas de probabilidade calibradas a partir de árvores de decisão e classificadores Bayesianos ingénuos, 2001.
- Aumentar os Diagramas de Fiabilidade, 2007.
API
- sklearn.calibration.CalibratedClassifierCV API
- sklearn.calibration.calibration_curve API
li>Calibração de Probabilidade, scikit-learn Guia do Utilizadorli> Curvas de Calibração de Probabilidade, scikit-learnli>Comparação de Calibração de Classificadores, scikit-learn
Artigos
- Site de verificação CAWCAR
- Calibração (estatística) na Wikipedia
- Classificação probabilística na Wikipedia
- Scikit forma correcta de calibrar classificadores com CalibratedClassifierCV em CrossValidated
Summary
Neste tutorial, descobriu a importância de calibrar as probabilidades previstas e como diagnosticar e melhorar a calibração dos modelos utilizados para a classificação probabilística.
Especificamente, aprendeu:
- Os algoritmos de aprendizagem de máquinas não lineares prevêem frequentemente probabilidades de classe não calibradas.
- Diagramas de fiabilidade podem ser usados para diagnosticar a calibração de um modelo, e os métodos podem ser usados para melhor calibrar as previsões para um problema.
- Como desenvolver diagramas de fiabilidade e calibrar modelos de classificação em Python com scikit-learn.
Têm alguma questão?
Saber as vossas questões nos comentários abaixo e farei o meu melhor para responder.
Confiram a Probabilidade para Aprendizagem de Máquinas!

Desenvolvam a vossa compreensão da Probabilidade
…com apenas algumas linhas de código python
Descobre como no meu novo Ebook:
Probabilidade para Aprendizagem de Máquinas
p>proporciona tutoriais de auto-estudo e projectos end-to-end em:
Theorem Bayes, Bayesian Optimization, Distributions, Maximum Likelihood, Cross-Entropy, Calibrating Models
e muito mais…
Finally Harness Uncertainty in Your Projects
Skip the Academics. Just Results.See What’s Inside