Drei grundlegende Eigenschaften des Gleichgewichts im Allgemeinen wurden von Huw Dixon vorgeschlagen. Diese sind:
Gleichgewichtseigenschaft P1: Das Verhalten der Agenten ist konsistent.
Gleichgewichtseigenschaft P2: Kein Agent hat einen Anreiz, sein Verhalten zu ändern.
Gleichgewichtseigenschaft P3: Das Gleichgewicht ist das Ergebnis eines dynamischen Prozesses (Stabilität).
Beispiel: WettbewerbsgleichgewichtBearbeiten

- P – Preis
- Q – nachgefragte und angebotene Menge
- S – Angebotskurve
- D – Nachfragekurve
- P0 – Gleichgewichtspreis
- A – Überschuss Nachfrage – wenn P<P0
- B – Angebotsüberschuss – wenn P>P0
In einem Wettbewerbsgleichgewicht, ist das Angebot gleich der Nachfrage. Eigenschaft P1 ist erfüllt, da zum Gleichgewichtspreis die angebotene Menge gleich der nachgefragten Menge ist. Die Eigenschaft P2 ist ebenfalls erfüllt. Die Nachfrage wird so gewählt, dass der Nutzen angesichts des Marktpreises maximiert wird: Niemand auf der Nachfrageseite hat einen Anreiz, zum herrschenden Preis mehr oder weniger zu verlangen. Ebenso wird das Angebot von den Unternehmen bestimmt, die ihre Gewinne zum Marktpreis maximieren: Kein Unternehmen wird zum Gleichgewichtspreis mehr oder weniger liefern wollen. Daher haben die Akteure weder auf der Nachfrage- noch auf der Angebotsseite einen Anreiz, ihre Handlungen zu ändern.
Um zu sehen, ob Eigenschaft P3 erfüllt ist, betrachten wir, was passiert, wenn der Preis über dem Gleichgewichtspreis liegt. In diesem Fall besteht ein Überangebot, d. h. die angebotene Menge übersteigt die nachgefragte. Dadurch wird der Preis tendenziell nach unten gedrückt, damit er zum Gleichgewicht zurückkehrt. Liegt der Preis unter dem Gleichgewichtspunkt, besteht eine Angebotsknappheit, die zu einem Preisanstieg führt, der den Gleichgewichtszustand wieder herstellt. Nicht alle Gleichgewichte sind „stabil“ im Sinne der Gleichgewichtseigenschaft P3. Es ist möglich, Wettbewerbsgleichgewichte zu haben, die instabil sind. Wenn ein Gleichgewicht jedoch instabil ist, stellt sich die Frage, wie es erreicht werden kann. Selbst wenn es die Eigenschaften P1 und P2 erfüllt, bedeutet das Fehlen von P3, dass sich der Markt nur dann im instabilen Gleichgewicht befinden kann, wenn er von dort ausgeht.
In den meisten einfachen mikroökonomischen Geschichten von Angebot und Nachfrage wird ein statisches Gleichgewicht in einem Markt beobachtet; das ökonomische Gleichgewicht kann jedoch auch dynamisch sein. Das Gleichgewicht kann auch gesamtwirtschaftlich oder allgemein sein, im Gegensatz zum partiellen Gleichgewicht eines einzelnen Marktes. Das Gleichgewicht kann sich ändern, wenn sich die Nachfrage- oder Angebotsbedingungen ändern. Zum Beispiel stört ein Anstieg des Angebots das Gleichgewicht, was zu niedrigeren Preisen führt. Letztendlich wird auf den meisten Märkten ein neues Gleichgewicht erreicht. Dann gibt es keine Veränderung des Preises oder der gekauften und verkauften Produktionsmenge – bis es zu einer exogenen Verschiebung des Angebots oder der Nachfrage kommt (z. B. Änderungen der Technologie oder des Geschmacks). Das heißt, es gibt keine endogenen Kräfte, die zum Preis oder zur Menge führen.
Beispiel: Nash-GleichgewichtBearbeiten
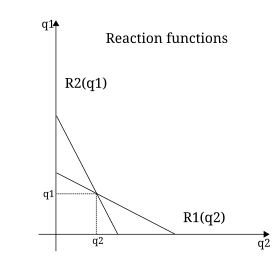
Das Nash-Gleichgewicht wird in den Wirtschaftswissenschaften häufig als Hauptalternative zum Wettbewerbsgleichgewicht verwendet. Es wird immer dann verwendet, wenn es ein strategisches Element im Verhalten der Agenten gibt und die „Preisübernahme“-Annahme des Wettbewerbsgleichgewichts unangemessen ist. Die erste Anwendung des Nash-Gleichgewichts war das Cournot-Duopol, das von Antoine Augustin Cournot in seinem Buch von 1838 entwickelt wurde. Beide Firmen produzieren ein homogenes Produkt: Angesichts der Gesamtmenge, die von den beiden Firmen geliefert wird, wird der (einzige) Branchenpreis anhand der Nachfragekurve bestimmt. Dieser bestimmt die Einnahmen jeder Firma (der Industriepreis mal die von der Firma gelieferte Menge). Der Gewinn jedes Unternehmens ergibt sich dann aus diesen Einnahmen abzüglich der Kosten für die Produktion des Outputs. Es besteht eindeutig eine strategische Interdependenz zwischen den beiden Unternehmen. Wenn eine Firma ihren Output variiert, wirkt sich dies wiederum auf den Marktpreis und damit auf die Einnahmen und Gewinne der anderen Firma aus. Wir können die Auszahlungsfunktion definieren, die den Gewinn jeder Firma als eine Funktion der beiden von den Firmen gewählten Outputs angibt. Cournot nahm an, dass jede Firma ihren eigenen Output so wählt, dass sie ihren Gewinn angesichts des Outputs der anderen Firma maximiert. Das Nash-Gleichgewicht tritt ein, wenn beide Firmen den Output produzieren, der ihren eigenen Gewinn unter Berücksichtigung des Outputs der anderen Firma maximiert.
In Bezug auf die Gleichgewichtseigenschaften können wir sehen, dass P2 erfüllt ist: In einem Nash-Gleichgewicht hat keine Firma einen Anreiz, vom Nash-Gleichgewicht unter Berücksichtigung des Outputs der anderen Firma abzuweichen. P1 ist erfüllt, da die Auszahlungsfunktion sicherstellt, dass der Marktpreis mit dem gelieferten Output konsistent ist und dass der Gewinn jedes Unternehmens bei diesem Output gleich dem Erlös abzüglich der Kosten ist.
Ist das Gleichgewicht stabil, wie von P3 gefordert? Cournot selbst argumentierte, dass es stabil ist, indem er das Stabilitätskonzept der Best-Response-Dynamik anwendet. Die Reaktionsfunktion für jedes Unternehmen gibt den Output an, der die Gewinne maximiert (best response), und zwar in Bezug auf den Output eines Unternehmens in Bezug auf einen gegebenen Output des anderen Unternehmens. Im Standard-Cournot-Modell ist dies abwärts gerichtet: Wenn das andere Unternehmen einen höheren Output produziert, besteht die beste Reaktion darin, weniger zu produzieren. Bei der Best-Response-Dynamik gehen die Unternehmen von einer beliebigen Position aus und passen dann ihren Output an ihre beste Reaktion auf den vorherigen Output des anderen Unternehmens an. Solange die Reaktionsfunktionen eine Steigung von weniger als -1 haben, wird dies zum Nash-Gleichgewicht konvergieren. Diese Stabilitätsgeschichte ist jedoch sehr kritisch zu sehen. Wie Dixon argumentiert: „Die entscheidende Schwäche ist, dass sich die Firmen bei jedem Schritt kurzsichtig verhalten: Sie wählen ihren Output, um ihre aktuellen Gewinne angesichts des Outputs der anderen Firma zu maximieren, ignorieren aber die Tatsache, dass der Prozess vorgibt, dass die andere Firma ihren Output anpassen wird…“. Es gibt noch andere Stabilitätskonzepte, die für das Nash-Gleichgewicht vorgeschlagen wurden, z. B. evolutionäre Stabilität.