Lernziele

  • Beschreiben Sie die Bewegung der gedämpften harmonischen Bewegung
  • Schreiben Sie die Bewegungsgleichungen für gedämpfte harmonische Schwingungen
  • Beschreiben Sie die Bewegung der getriebenen, oder erzwungenen, gedämpften harmonischen Bewegung
  • Beschreiben Sie die Bewegungsgleichungen für erzwungene, gedämpfte harmonische Bewegung

In der realen Welt folgen Schwingungen selten einer echten SHM. Reibung irgendeiner Art dämpft normalerweise die Bewegung, so dass sie abklingt oder mehr Kraft benötigt, um fortzufahren. In diesem Abschnitt werden wir einige Beispiele für gedämpfte harmonische Bewegungen untersuchen und sehen, wie man die Bewegungsgleichungen modifizieren kann, um diesen allgemeineren Fall zu beschreiben.

Eine Gitarrensaite hört einige Sekunden nach dem Anzupfen auf zu schwingen. Um auf einer Spielplatzschaukel weiter zu schwingen, muss man weiter schieben (Abbildung \(\PageIndex{1}\)). Obwohl wir die Reibung und andere nicht-konservative Kräfte oft klein oder vernachlässigbar machen können, ist eine völlig ungedämpfte Bewegung selten. Tatsächlich möchten wir vielleicht sogar Schwingungen dämpfen, wie bei Stoßdämpfern im Auto.

Ein Foto von einer Person auf einer Schaukel
Abbildung \(\PageIndex{1}\): Um den dämpfenden Kräften entgegenzuwirken, müssen Sie eine Schaukel immer wieder aufpumpen. (credit: Bob Mical)

Abbildung \(\PageIndex{2}\) zeigt eine Masse m, die an einer Feder mit einer Kraftkonstante k befestigt ist. Die Masse wird bis zu einer Position A0, der Anfangsamplitude, angehoben und dann losgelassen. Die Masse schwingt um die Gleichgewichtslage in einer Flüssigkeit mit Viskosität, wobei die Amplitude bei jeder Schwingung abnimmt. Für ein System mit einer geringen Dämpfung sind die Periode und die Frequenz konstant und entsprechen nahezu der SHM, aber die Amplitude nimmt wie gezeigt allmählich ab. Dies geschieht, weil die nicht-konservative Dämpfungskraft dem System Energie entzieht, normalerweise in Form von thermischer Energie.

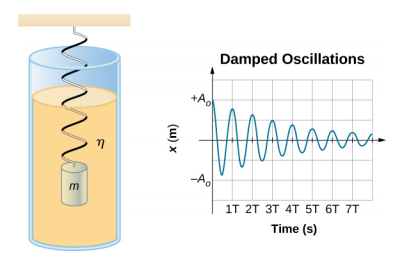
Eine Masse m ist an einer vertikalen Feder aufgehängt und in eine Flüssigkeit mit der Viskosität eta eingetaucht. Ein Graph der gedämpften Schwingung zeigt die Auslenkung x in Metern auf der vertikalen Achse als Funktion der Zeit in Sekunden auf der horizontalen Achse. Der Bereich von x reicht von minus A sub Null bis plus A sub Null. Die Zeitskala reicht von Null bis 7 T, mit Ticks in Schritten von T. Die Auslenkung ist zum Zeitpunkt Null plus A sub Null und oszilliert zwischen positiven Maxima und negativen Minima, wobei jeder volle Zyklus die gleiche Zeit T benötigt, aber die Amplitude der Schwingungen mit der Zeit abnimmt.
Abbildung: Bei einer Masse an einer Feder, die in einer viskosen Flüssigkeit schwingt, bleibt die Periode konstant, aber die Amplituden der Schwingungen nehmen aufgrund der Dämpfung durch die Flüssigkeit ab.

Betrachten Sie die auf die Masse wirkenden Kräfte. Beachten Sie, dass der einzige Beitrag der Masse darin besteht, die Gleichgewichtslage zu verändern, wie bereits weiter oben im Kapitel besprochen. Daher ist die Nettokraft gleich der Kraft der Feder und der Dämpfungskraft (\(F_D\)). Wenn der Betrag der Geschwindigkeit klein ist, d. h. die Masse schwingt langsam, ist die Dämpfungskraft proportional zur Geschwindigkeit und wirkt entgegen der Bewegungsrichtung (\(F_D = -b\)). Die Nettokraft auf die Masse ist daher

Schreibt man dies als Differentialgleichung in x, erhält man

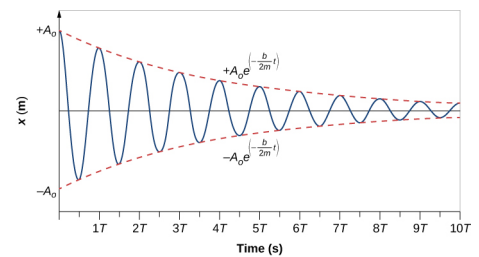
Um die Lösung dieser Gleichung zu bestimmen, betrachten Sie den in Abbildung \(\PageIndex{3}\) gezeigten Verlauf von Position gegen Zeit. Die Kurve ähnelt einer Kosinuskurve, die in der Einhüllenden einer Exponentialfunktion \(A_0e^{-\alpha t}\) schwingt, wobei \(\alpha = \frac{b}{2m}\). Die Lösung ist

Es bleibt als Übung, zu beweisen, dass dies tatsächlich die Lösung ist. Um zu beweisen, dass es die richtige Lösung ist, nimmt man die erste und zweite Ableitung nach der Zeit und setzt sie in Gleichung 15.23 ein. Es zeigt sich, dass Gleichung 15.24 die Lösung ist, wenn

Erinnern Sie sich, dass die Winkelfrequenz einer Masse, die einer SHM unterliegt, gleich der Quadratwurzel der Kraftkonstante geteilt durch die Masse ist. Dies wird oft als die Eigenwinkelfrequenz bezeichnet, die wie folgt dargestellt wird

Die Winkelfrequenz für eine gedämpfte harmonische Bewegung wird

Die Abbildung zeigt ein Diagramm der Verschiebung, x in Metern, entlang der vertikalen Achse, gegen die Zeit in Sekunden entlang der horizontalen Achse. Die Verschiebung reicht von minus A sub Null bis plus A sub Null und die Zeit reicht von 0 bis 10 T. Die Verschiebung, dargestellt durch eine blaue Kurve, oszilliert zwischen positiven Maxima und negativen Minima und bildet eine Welle, deren Amplitude allmählich abnimmt, je weiter man sich von t=0 entfernt. Die Zeit, T, zwischen benachbarten Scheitelpunkten bleibt immer gleich. Die Hüllkurve, die glatte Kurve, die die Scheitelpunkte und eine weitere glatte Kurve, die die Tiefpunkte der Schwingungen verbindet, ist als gestrichelte rote Linienpaar dargestellt. Die obere Kurve, die die Scheitelpunkte verbindet, ist beschriftet als plus A sub Null mal e bis zur Menge minus b t über 2 m. Die untere Kurve, die die Tiefpunkte verbindet, ist beschriftet als minus A sub Null mal e bis zur Menge minus b t über 2 m.
Abbildung \(\PageIndex{3}\): Position über der Zeit für die an einer Feder schwingende Masse in einer viskosen Flüssigkeit. Beachten Sie, dass die Kurve eine Kosinusfunktion innerhalb einer exponentiellen Hüllkurve zu sein scheint.

Erinnern Sie sich, dass wir zu Beginn dieser Beschreibung der gedämpften harmonischen Bewegung festgestellt haben, dass die Dämpfung klein sein muss. Zwei Fragen drängen sich auf. Warum muss die Dämpfung klein sein? Und wie klein ist klein? Wenn Sie die Dämpfung in einem System allmählich erhöhen, beginnen sich Periode und Frequenz zu verändern, weil die Dämpfung der Hin- und Herbewegung entgegenwirkt und sie somit verlangsamt. (Die Nettokraft ist in beiden Richtungen kleiner.) Bei sehr großer Dämpfung schwingt das System gar nicht mehr – es bewegt sich langsam in Richtung Gleichgewicht. Die Kreisfrequenz ist gleich

Wenn b zunimmt, wird \(\frac{k}{m} – \left(\dfrac{b}{2m}\right)^{2}\) kleiner und erreicht schließlich Null, wenn b = \(\sqrt{4mk}\). Wenn b noch größer wird, wird \(\frac{k}{m} – \left(\dfrac{b}{2m}\right)^{2}\) eine negative Zahl und \(\sqrt{\frac{k}{m} – \left(\dfrac{b}{2m}\right)^{2}}) ist eine komplexe Zahl.

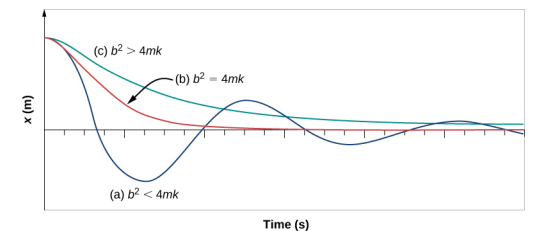
Die Position, x in Metern auf der vertikalen Achse, gegen die Zeit in Sekunden auf der horizontalen Achse, mit unterschiedlichen Graden der Dämpfung. Für beide Achsen ist keine Skala angegeben. Alle drei Kurven beginnen an der gleichen positiven Position zum Zeitpunkt Null. Die blaue Kurve a, beschriftet mit b zum Quadrat ist kleiner als 4 m k, durchläuft etwas mehr als zweieinviertel Schwingungen mit abnehmender Amplitude und konstanter Periode. Die rote Kurve b, beschriftet mit b zum Quadrat ist gleich 4 m k, fällt bei t=0 weniger schnell ab als die blaue Kurve, oszilliert aber nicht. Die rote Kurve nähert sich asymptotisch x=0 und ist innerhalb einer Schwingung der blauen Kurve nahezu Null. Die grüne Kurve c, beschriftet mit b zum Quadrat, ist größer als 4 m k, fällt bei t=0 weniger schnell ab als die rote Kurve und oszilliert nicht. Die grüne Kurve nähert sich asymptotisch x=0, liegt aber am Ende der Grafik, nach mehr als zwei Oszillationen der blauen Kurve, immer noch deutlich über Null.
Abbildung \(\PageIndex{4}\): Die Position über der Zeit für drei Systeme, bestehend aus einer Masse und einer Feder in einer viskosen Flüssigkeit. (a) Wenn die Dämpfung klein ist (b < \(\sqrt{4mk}\)), oszilliert die Masse und verliert langsam an Amplitude, da die Energie durch die nicht konservierende(n) Kraft(en) dissipiert wird. Der Grenzfall ist (b), wenn die Dämpfung (b = \(\sqrt{4mk}\)) ist. (c) Wenn die Dämpfung sehr groß ist (b > \(\sqrt{4mk}\)), schwingt die Masse bei einer Verschiebung nicht, sondern versucht, in die Gleichgewichtslage zurückzukehren.

Abbildung \(\PageIndex{4}\) zeigt die Auslenkung eines harmonischen Oszillators für verschiedene Beträge der Dämpfung.

  1. Wenn die Dämpfungskonstante klein ist, b < \(\sqrt{4mk}\), schwingt das System, während die Amplitude der Bewegung exponentiell abfällt. Dieses System wird als unterdämpft bezeichnet, wie in Kurve (a). Viele Systeme sind unterdämpft und schwingen, während die Amplitude exponentiell abnimmt, wie z. B. die Masse, die auf einer Feder schwingt. Die Dämpfung kann recht klein sein, aber schließlich kommt die Masse zur Ruhe.
  2. Wenn die Dämpfungskonstante \(b = \sqrt{4mk}\) ist, wird das System als kritisch gedämpft bezeichnet, wie in Kurve (\(b\)). Ein Beispiel für ein kritisch gedämpftes System sind die Stoßdämpfer in einem Auto. Es ist von Vorteil, wenn die Schwingungen so schnell wie möglich abklingen. Hier schwingt das System nicht, sondern nähert sich asymptotisch so schnell wie möglich dem Gleichgewichtszustand.
  3. Kurve (c) in Abbildung \(\PageIndex{4}\) stellt ein überdämpftes System dar, bei dem \(b > \sqrt{4mk}\). Ein überdämpftes System nähert sich dem Gleichgewicht über einen längeren Zeitraum an.

Eine kritische Dämpfung ist oft erwünscht, da ein solches System schnell ins Gleichgewicht zurückkehrt und auch im Gleichgewicht bleibt. Außerdem bringt eine konstante Kraft, die auf ein kritisch gedämpftes System ausgeübt wird, das System in kürzester Zeit in eine neue Gleichgewichtslage, ohne dass es überschwingt oder um die neue Lage schwingt.

Übungsaufgabe \(\PageIndex{1}\)

Warum sind völlig ungedämpfte harmonische Oszillatoren so selten?

Beitragende und Namensnennung

  • Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University) und Bill Moebs mit vielen beitragenden Autoren. Dieses Werk ist lizenziert von OpenStax University Physics unter einer Creative Commons Attribution License (by 4.0).

By: adminPosted on

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert.