In diesem Tutorial werden wir über den aktiven Bandpassfilter, seinen Frequenzgang, Typen, Beispiele und vieles mehr lernen. In einem früheren Tutorium haben wir uns mit Bandpassfiltern beschäftigt, aber der Entwurfsansatz in diesem Tutorium basierte auf passiven Komponenten.
Bandpassfilter können, wie jedes andere Filter, mit aktiven Komponenten wie Transistoren und Operationsverstärkern entworfen werden. Wenn Sie mehr über passive Bandpassfilter wissen wollen, lesen Sie „Passive Bandpass-RC-Filter“.
Übersicht
Einführung
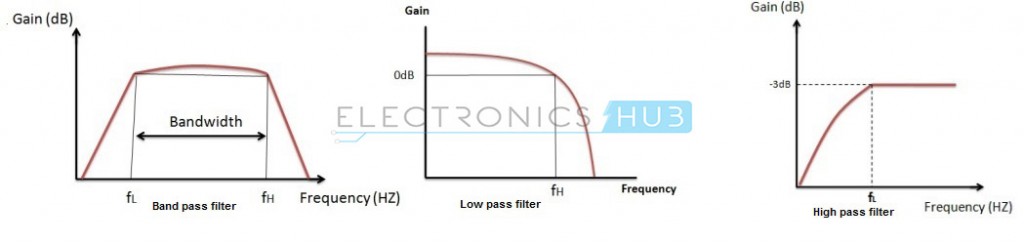
Ein Bandpassfilter ist eine Schaltung, die nur ein bestimmtes Frequenzband durchlässt. Dieses Passband liegt hauptsächlich zwischen den Grenzfrequenzen und diese sind fL und fH, wobei fL die untere Grenzfrequenz und fH die obere Grenzfrequenz ist.
Die Mittenfrequenz wird mit ‚fC‘ bezeichnet und wird auch als Resonanzfrequenz oder Spitzenfrequenz bezeichnet.
Der Wert von fL muss immer kleiner sein als der Wert von fH. Der Durchlassbereich des Filters ist nichts anderes als die Bandbreite. Die Verstärkung des Filters ist bei der Resonanz- oder Mittenfrequenz maximal und wird als Gesamt-Durchlassbereichsverstärkung bezeichnet. Diese Durchlassbandverstärkung wird mit ‚Amax‘ bezeichnet.
Bei Tiefpassfiltern beginnt das Durchlassband bei 0 Hz und reicht bis zur Resonanzfrequenz bei -3 dB unterhalb der maximalen Durchlassbandverstärkung.
Beim Hochpassfilter beginnt dieses Durchlassband bei der -3-dB-Resonanzfrequenz und endet bei dem Wert der maximalen Schleifenverstärkung für das aktive Filter. Die Kombination von Tiefpass- und Hochpassverhalten ergibt das unten gezeigte Bandpassverhalten:
ZURÜCK ZUM OBENEN
Aktives Bandpassfilter
Abhängig vom Gütefaktor wird das Bandpassfilter in Breitband- und Schmalbandfilter unterteilt. Der Gütefaktor wird auch als „figure of merit“ bezeichnet. Durch Kaskadierung von Hochpassfilter und Tiefpassfilter mit einem verstärkenden Bauteil erhält man ein Bandpassfilter.

Die Verstärkerschaltung zwischen diesen Hochpass- und Tiefpassfiltern sorgt für die Isolierung und gibt der Schaltung eine Gesamtverstärkung. Die Werte der Grenzfrequenzen der beiden Filter müssen mit minimaler Differenz eingehalten werden.
Wenn diese Differenz sehr klein ist, kann es zu einer Interaktion von Hoch- und Tiefpassstufen kommen. Um die richtigen Pegel dieser Grenzfrequenzen zu erhalten, ist daher eine Verstärkerschaltung erforderlich.
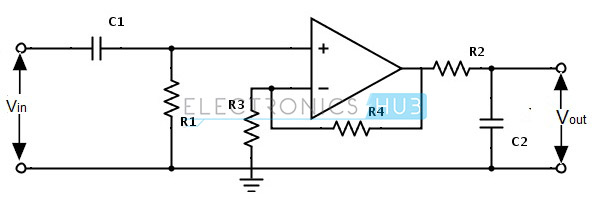
Das Schaltbild für ein aktives Bandpassfilter ist unten dargestellt:
ZURÜCK ZUM OBENEN
Breitbandpassfilter
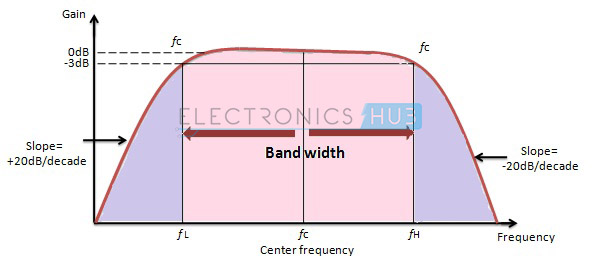
Wenn der Wert des Qualitätsfaktors kleiner als zehn ist, dann ist das Durchlassband breit, was uns eine größere Bandbreite gibt. Dieses Bandpassfilter wird Wide Band Pass Filter genannt.
In diesem Filter muss die hohe Grenzfrequenz größer sein als die untere Grenzfrequenz. Es verwendet zwei verstärkende Elemente (Op-Amps) in der Konstruktion.
Zuerst durchläuft das Signal den Hochpassfilter, das Ausgangssignal dieses Hochpassfilters tendiert gegen unendlich und somit wird das gegen unendlich tendierende Signal am Ende an den Tiefpassfilter gegeben.
Dieser Tiefpassfilter lässt das Hochfrequenzsignal tief durch.
Wenn der Hochpassfilter mit dem Tiefpassfilter kaskadiert wird, erhält man den einfachen Bandpassfilter. Um dieses Filter zu realisieren, muss die Reihenfolge der Tiefpass- und Hochpassschaltungen gleich sein.
Durch Kaskadierung eines Tiefpasses und eines Hochpasses erster Ordnung erhalten wir das Bandpassfilter zweiter Ordnung und durch Kaskadierung von zwei Tiefpassfiltern erster Ordnung mit zwei Hochpassfiltern entsteht ein Bandpassfilter vierter Ordnung.
Durch diese Kaskadierung ergibt die Schaltung einen geringen Gütefaktor. Der Kondensator im Hochpassfilter erster Ordnung blockiert jegliche Gleichstromvorspannung aus dem Eingangssignal.
Die Verstärkung rollt an den beiden Stoppbändern ab und beträgt im Fall des Filters zweiter Ordnung (High + Low) ± 20 dB /Dekade. Die Hochpass- und Tiefpassfilter dürfen nur erster Ordnung sein.
Wenn die Hochpass- und Tiefpassfilter zweiter Ordnung sind, dann beträgt der Verstärkungsabfall an beiden Stoppbändern ± 40 dB/Dekade.
Der Ausdruck für die Spannungsverstärkung des Bandpassfilters lautet:
| Vout / Vin | = / √{}
Er ergibt sich aus den individuellen Verstärkungen des Hochpass- und des Tiefpassfilters, die individuellen Verstärkungen des Hochpass- und des Tiefpassfilters sind unten angegeben.
Spannungsverstärkung für Hochpassfilter:
| Vout / Vin | = / √
Spannungsverstärkung für Tiefpassfilter:
| Vout / Vin | = Amax2 / √
Amax = Amax1 * Amax2
Wobei Amax1 die Verstärkung der Hochpassstufe und Amax2 die Verstärkung der Tiefpassstufe ist.
Der Frequenzgang des Breitbandfilters ist unten dargestellt.
ZURÜCK NACH OBEN
Schmalband-Passfilter
Wenn der Wert des Qualitätsfaktors größer als zehn ist, dann ist das Durchlassband schmal und die Bandbreite des Durchlassbandes ist ebenfalls geringer. Dieses Bandpassfilter wird als Schmalbandpassfilter bezeichnet.
Es verwendet nur ein aktives Bauteil (Operationsverstärker) anstelle von zwei und dieser Operationsverstärker ist in invertierender Konfiguration. In diesem Filter ist die Verstärkung des Operationsverstärkers bei der Mittenfrequenz fc maximal.
ZURÜCK NACH OBEN
Schmalbandpassfilter-Schaltung
Der Eingang liegt an der invertierenden Eingangsklemme an. Dies zeigt, dass der Operationsverstärker in invertierender Konfiguration arbeitet. Diese Filterschaltung erzeugt ein Schmalbandpassfilterverhalten.

Die Spannungsverstärkung der obigen Filterschaltung ist AV = – R2 / R1
Die Grenz-Off-Frequenzen der Filterschaltung sind
fC1 = 1 / (2πR1C1) und fC2 = 1 / (2πR2C2)
ZURÜCK NACH OBEN
Mehrfach rückgekoppeltes aktives Bandpassfilter
Diese Filterschaltung ergibt einen abgestimmten Kreis, der auf der Gegenkopplung des Filters basiert. Der wichtige Vorteil dieser mehrfachen Rückkopplung ist, dass wir ohne Änderung der maximalen Verstärkung bei der Mittenfrequenz den Wert der Grenzfrequenz ändern können. Diese Änderung der Grenzfrequenz kann über den Widerstand ‚R3‘ erfolgen.
Betrachten wir die untenstehende aktive Filterschaltung, betrachten wir den geänderten Widerstandswert als R3′und den geänderten Wert der Grenzfrequenz als fc′, dann können wir für den neuen Widerstandswert wie folgt gleichsetzen:
R3′ = R3(fc /fc′)²
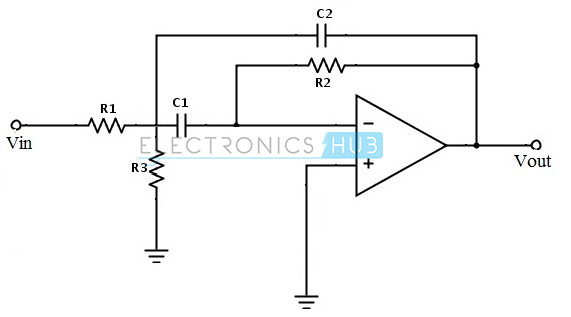
Es besteht aus zwei Rückkopplungspfaden, wegen dieser mehreren Rückkopplungspfade wird es auch als „Bandpassschaltung mit mehreren Rückkopplungen“ bezeichnet. Diese Schaltung erzeugt ein mehrfach rückgekoppeltes Bandpassfilter mit unendlicher Verstärkung. Durch diese Schaltung erhöht sich der Gütefaktorwert maximal bis auf 20.
fc = 1/√(R1R2C1C2)
Q = fc/Bandbreite = (½){√}
Amax = -R2/2R1
R1 = Q/{2πfcCAmax}
R2 = Q/πfcC
R3 = Q/{2πfcC(2Q² – Amax)}
Die Verstärkung bei der Mittenfrequenz ‚Amax‘ muss kleiner als 2Q² sein. Das heißt,
Amax < 2Q²
Wobei,
fc = Grenzfrequenz in Hz
C = Kapazität, (C1 = C2 = C)
Q = Gütefaktor
Amax = Maximale Verstärkung
ZURÜCK ZUM TOP
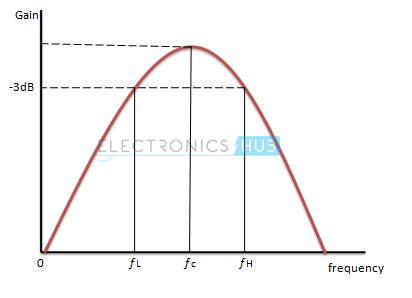
Der Frequenzgang eines aktiven Bandpassfilters
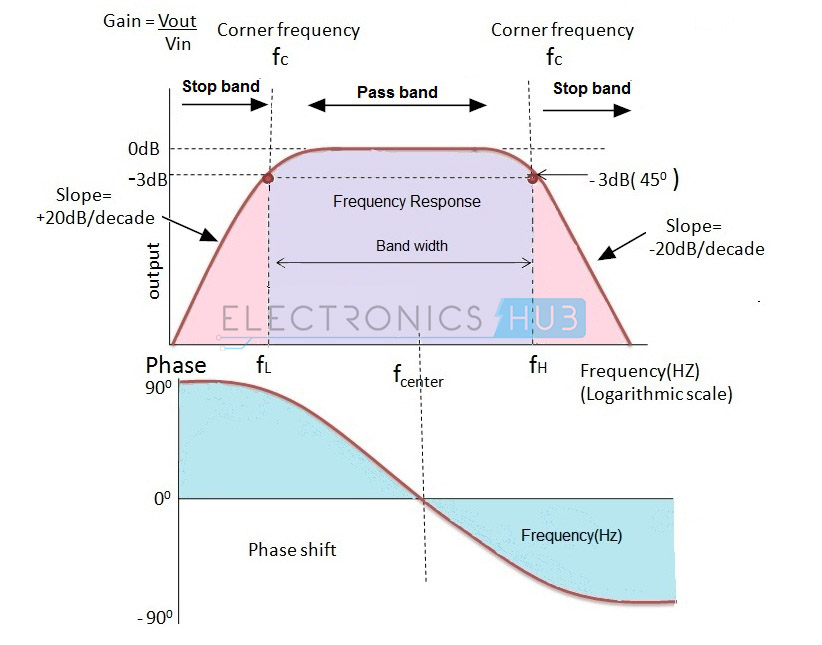
Es hat zwei Mittenfrequenzen, eine des Hochpassfilters und die andere des Tiefpassfilters. Die Mittenfrequenz des Hochpassfilters muss niedriger sein als die Mittenfrequenz des Tiefpassfilters.
Die Mittenfrequenz des Bandpassfilters ist das geometrische Mittel aus unterer und oberer Grenzfrequenz fr2 = fH * fL.
Die Verstärkung des Filters beträgt 20 log (Vout/Vin) dB/Dekade. Der Amplitudengang ist ähnlich dem des Tiefpass- und Hochpassfilters. Je nach Kaskadierung der Filterreihenfolge ändert sich die Kennlinie.
Die normierte Mittenfrequenz ist mit fr = 1 gegeben. Betrachten wir zwei Grenzfrequenzen als 300 Hz und 900 Hz, dann ist die Bandbreite des Filters 300 Hz -900 Hz = 600 Hz.
ZURÜCK ZUM TOP
Der Gütefaktor
Der Gütefaktor hängt von der Bandbreite des Durchlassbereichs ab. Der Qualitätsfaktor ist umgekehrt proportional zur Bandbreite. Das heißt, wenn die Bandbreite zunimmt, sinkt der Qualitätsfaktor und wenn die Bandbreite abnimmt, steigt der Qualitätsfaktor.
Q = fc/Bandbreite
Für breitbandige Durchlassfilter ist der Qualitätsfaktor niedrig, weil die Durchlassbandbreite hoch ist. Beim Schmalbandpassfilter ist der Gütefaktor hoch. Selektivität und Unselektivität hängen von der Breite des Durchlassbandes ab.
Dieser Qualitätsfaktor hängt auch mit dem Dämpfungsfaktor () zusammen. Je höher der Wert des Dämpfungsfaktors ist, desto flacher ist auch die Ausgangsantwort. Dies wird wie folgt gleichgesetzt:
ε = 2/Q
Für verschiedene Werte des Gütefaktors ist die normierte Verstärkungsantwort eines Bandpassfilters zweiter Ordnung gegeben als:
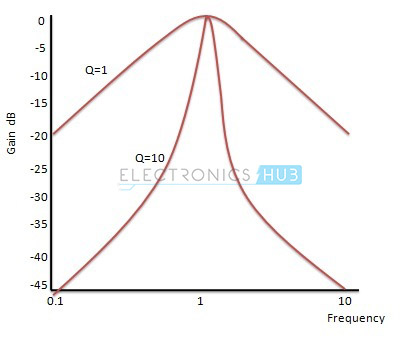
Aus diesem Diagramm ist ersichtlich, dass die Selektivität für einen höheren Gütefaktor größer ist.
ZURÜCK ZUM OBENEN
Beispiel für ein aktives Bandpassfilter
Betrachten wir eine aktive Filterschaltung mit unendlicher Verstärkung und mehrfacher Rückkopplung, bei der die Resonanzfrequenz 1.5 kHz, die maximale Spannungsverstärkung ist 15 und der Gütefaktor ist 7. Dann werden die Komponentenwerte wie folgt berechnet:
Für Widerstände
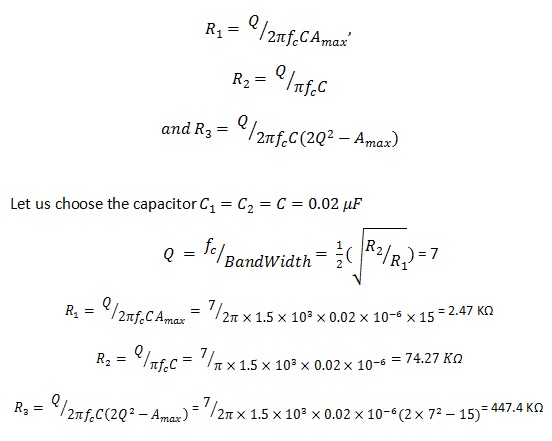
Wenn wir den geänderten Widerstandswert als R3′ und den geänderten Grenzfrequenzwert fc’=2 KHz betrachten, können wir für den neuen Widerstandswert wie folgt gleichsetzen: