Braggsches Gesetz

قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).

Definition

Das Braggsche Gesetz gibt die Bedingung an, dass eine ebene Welle an einer Familie von Gitterebenen gebeugt wird:

2 d sin θ = n λ

wobei d der Abstand zwischen den Ebenen ist, θ der Winkel zwischen dem Wellenvektor der einfallenden ebenen Welle, ko, und den Gitterebenen, λ ihre Wellenlänge und n eine ganze Zahl, die Ordnung der Reflexion. Es ist äquivalent zur Beugungsbedingung im reziproken Raum und zu den Laue-Gleichungen.

Direkte Herleitung des Braggschen Gesetzes

Reflexion an der ersten Ebene

Die gestreuten Wellen sind unabhängig von der Verteilung der Punktstreuer in der ersten Ebene phasengleich, wenn der Winkel des reflektierten Wellenvektors, kh, ebenfalls gleich θ ist. Dies ist das Snell-Descartes’sche Reflexionsgesetz.

Reflexion an der zweiten Ebene

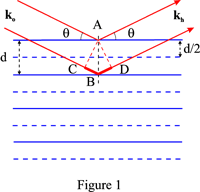
Da die Phase der reflektierten Wellen unabhängig von der Position des Punktstreuers in der Ebene ist, erhält man die Phasendifferenz zwischen den von zwei aufeinanderfolgenden Gitterebenen reflektierten Wellen, indem man willkürlich einen Streupunkt A in der ersten Ebene und einen Streupunkt B in der zweiten Ebene so wählt, dass AB senkrecht zu den Ebenen steht. Wenn C und D die Projektionen von A auf die einfallenden und reflektierten Wellenvektoren sind, die durch B gehen, ist aus Abbildung 1 ersichtlich, dass der Wegunterschied zwischen den an A bzw. B reflektierten Wellen ist:

CB + BD = 2d sin θ

und dass die beiden Wellen in Phase sind, wenn diese Wegdifferenz gleich nλ ist, wobei n eine ganze Zahl ist.

Reflexion an der dritten usw. Ebene

Wenn die Braggsche Beziehung für die ersten beiden Ebenen erfüllt ist, werden die mit dem Wellenvektor kh reflektierten Wellen für alle Ebenen der Familie in Phase sein.

Ordnung der Reflexion

Das Braggsche Gesetz kann auch geschrieben werden:

2 (d/n) sin θ = λ.

Man kann dann sagen, dass eine Bragg-Reflexion der Ordnung n an einer Familie von Gitterebenen der Ordnung n äquivalent ist zu einer Reflexion der Ordnung 1 an einer Familie von fiktiven oder imaginären Ebenen mit Gitterabstand

d_{hkl} = d/n.

Diese fiktive Familie ist mit dem reziproken Gittervektor OH verbunden, wobei OH = n/d = 1/d_{hkl}. Die Indizes der Spiegelung sind hkl. Zum Beispiel entsprechen die gestrichelten horizontalen Linien in Abbildung 1 den fiktiven Ebenen, die der zweiten Ordnung, n = 2, zugeordnet sind.

Reflexionsbedingungen

Wenn es eine Gleitebene oder eine Schraubenachse senkrecht zu den Gitterebenen gibt, ist der Abstand der eigentlichen Reflexionsebenen d/2 für eine Gleitebene und (d p/q) für eine qp-Schraubenachse. Das Braggsche Gesetz sollte dann geschrieben werden:

2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ

für eine Gleitebene und

2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ

für eine Schraubenachse qp.

Die Reflexionen ungerader Ordnung für eine Gleitebene und anderer Ordnung als (q/p)n für eine Schraubenachse sind dann abwesend. Man spricht von systematischen Abwesenheiten, die mit dem Vorhandensein von Gleit- oder Schraubenkomponenten zusammenhängen.

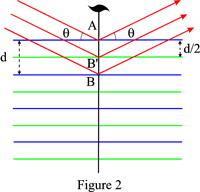
Als Beispiel zeigt Abbildung 2 den Fall einer 21-Schrauben-Achse: Die reflektierenden Ebenen sind die blauen Ebenen und die grünen Ebenen, die von letzteren durch die Wirkung der Schraubenachse abgeleitet werden. Reflexe ungerader Ordnung werden systematisch fehlen.

Einfluss der Verformung

Eine Verformung, die eine Familie von Gitterebenen (hkl) unverzerrt und ihren Gitterabstand d unverändert lässt, hat keinen Einfluss auf den Bragg-Winkel von kkl-Reflexen, z.

Geschichte

Bragg (1890-1971) präsentierte seine Herleitung der Reflexionsbedingung bei einem Treffen der Cambridge Philosophical Society am 11. November 1912. Sein Papier wurde 1913 veröffentlicht. Für Details siehe P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Abschnitt 5, S. 64 und A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Abschnitt 6.11, S. 120.