Hallo Glenn,

Ich gehe davon aus, dass Sie es mit einem regelmäßigen Achteck zu tun haben.

Zuerst musst du wissen, wie viele Diagonalen ein regelmäßiges Achteck hat und dann, wie viele davon die längste Länge haben. Zeichnen Sie ein Achteck, wählen Sie einen Scheitelpunkt und konstruieren Sie jede Diagonale von diesem Scheitelpunkt aus.

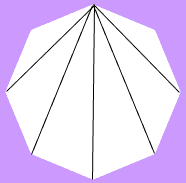
Damit können Sie für jeden der 8 Scheitelpunkte 5 Diagonalen zeichnen und haben somit 5 8 = 40 Diagonalen konstruiert. Aber Sie haben jede Diagonale zweimal konstruiert, einmal von jedem ihrer Enden aus. Es gibt also 20 Diagonalen in einem regelmäßigen Achteck.

Ein Blick auf das Diagramm oben zeigt, dass eine der konstruierten Diagonalen länger ist als die anderen. Man konstruiert also von jedem Scheitelpunkt eine lange Diagonale, also 8 lange Diagonalen. Wiederum haben Sie jede zweimal konstruiert, so dass es 4 lange Diagonalen gibt. Wenn man also eine Diagonale aus allen Diagonalen eines regelmäßigen Achtecks auswählt, gibt es 4 von 20 Chancen, dass man eine der längsten Diagonalen auswählt, und damit eine Wahrscheinlichkeit von 4/20 = 1/5.

Wie sieht es mit der kürzesten aus?

Andrei und Penny