Ein schrittweises Backpropagation-Beispiel - Matt Mazur

Hintergrund

Backpropagation ist eine gängige Methode zum Trainieren eines neuronalen Netzwerks. Es gibt keinen Mangel an Abhandlungen im Internet, die zu erklären versuchen, wie Backpropagation funktioniert, aber nur wenige, die ein Beispiel mit tatsächlichen Zahlen enthalten. Dieser Beitrag ist mein Versuch, die Funktionsweise anhand eines konkreten Beispiels zu erklären, mit dem die Leute ihre eigenen Berechnungen vergleichen können, um sicherzustellen, dass sie Backpropagation richtig verstehen.

Backpropagation in Python

Sie können mit einem Python-Skript herumspielen, das ich geschrieben habe und das den Backpropagation-Algorithmus in diesem Github Repo implementiert.

Visualisierung der Backpropagation

Für eine interaktive Visualisierung, die zeigt, wie ein neuronales Netzwerk lernt, schauen Sie sich meine Visualisierung des neuronalen Netzwerks an.

Zusätzliche Ressourcen

Wenn Sie dieses Tutorial nützlich finden und weiter über neuronale Netzwerke, maschinelles Lernen und Deep Learning lernen wollen, empfehle ich Ihnen das neue Buch von Adrian Rosebrock, Deep Learning for Computer Vision with Python. Ich habe das Buch wirklich genossen und werde bald eine vollständige Rezension veröffentlichen.

Übersicht

Für dieses Tutorial werden wir ein neuronales Netzwerk mit zwei Eingängen, zwei versteckten Neuronen und zwei Ausgangsneuronen verwenden. Zusätzlich werden die versteckten Neuronen und die Ausgangsneuronen einen Bias enthalten.

Hier ist die Grundstruktur:

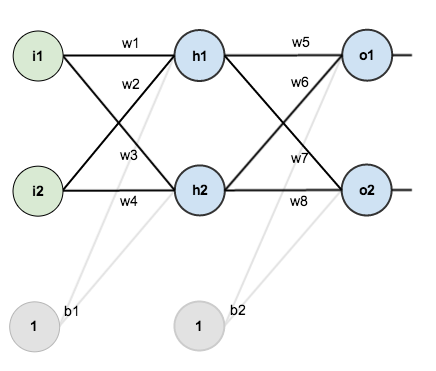
Neuronales_Netz (7)

Um ein paar Zahlen zum Arbeiten zu haben, sind hier die anfänglichen Gewichte, die Verzerrungen und die Trainingsinputs/-outputs:

Neuronales_Netz (9)

Das Ziel der Backpropagation ist es, die Gewichte zu optimieren, damit das neuronale Netz lernen kann, wie es beliebige Eingaben korrekt auf Ausgaben abbildet.

Für den Rest dieses Tutorials werden wir mit einem einzigen Trainingsset arbeiten: Bei Eingaben von 0,05 und 0,10 soll das neuronale Netz 0,01 und 0,99 ausgeben.

Der Vorwärtsdurchlauf

Zu Beginn sehen wir uns an, was das neuronale Netz bei den obigen Gewichten und Verzerrungen und den Eingaben von 0,05 und 0,10 derzeit vorhersagt. Dazu werden wir diese Eingaben vorwärts durch das Netz leiten.

Wir ermitteln die gesamte Netzeingabe für jedes Neuron der versteckten Schicht, zerquetschen die gesamte Netzeingabe mithilfe einer Aktivierungsfunktion (hier verwenden wir die logistische Funktion) und wiederholen den Vorgang dann mit den Neuronen der Ausgabeschicht.

Die Gesamtnetzeingabe wird in einigen Quellen auch als reine Netzeingabe bezeichnet.

Hier sehen Sie, wie wir die Gesamtnetzeingabe für $h_1$ berechnen:

$net_{h1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1$

$net_{h1} = 0.15 * 0.05 + 0.2 * 0.1 + 0.35 * 1 = 0.3775$

Wir zerlegen es dann mit der logistischen Funktion, um die Ausgabe von $h_1$ zu erhalten:

$out_{h1} = \frac{1}{1+e^{-net_{h1}}} = \frac{1}{1+e^{-0.3775}} = 0.593269992$

Wenn man den gleichen Prozess für $h_2$ durchführt, erhält man:

$out_{h2} = 0.596884378$

Wir wiederholen diesen Vorgang für die Neuronen der Ausgabeschicht und verwenden die Ausgaben der Neuronen der versteckten Schicht als Eingaben.

Hier ist die Ausgabe für $o_1$ :

$Netz_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1$

$net_{o1} = 0,4 * 0,593269992 + 0,45 * 0,596884378 + 0,6 * 1 = 1.105905967$

$out_{o1} = \frac{1}{1+e^{-net_{o1}}} = \frac{1}{1+e^{-1.105905967}} = 0.75136507$

Und wenn wir den gleichen Prozess für $o_2$ durchführen, erhalten wir:

$out_{o2} = 0.772928465$

Berechnen des Gesamtfehlers

Wir können nun den Fehler für jedes Ausgangsneuron mit Hilfe der quadratischen Fehlerfunktion berechnen und diese addieren, um den Gesamtfehler zu erhalten:

$E_{Gesamt} = \sum \frac{1}{2}(target - output)^{2}$

Einige Quellen bezeichnen das Ziel als das Ideal und den Ausgang als das Ist.

Das $\frac{1}{2}$ ist enthalten, damit der Exponent beim späteren Differenzieren aufgehoben wird. Das Ergebnis wird schließlich ohnehin mit einer Lernrate multipliziert, so dass es keine Rolle spielt, dass wir hier eine Konstante einführen.

Zum Beispiel ist die Zielausgabe für $o_1$ 0.01, aber die Ausgabe des neuronalen Netzwerks 0,75136507, daher ist sein Fehler:

$E_{o1} = \frac{1}{2}(target_{o1} - out_{o1})^{2} = \frac{1}{2}(0.01 - 0.75136507)^{2} = 0.274811083$

Wenn wir diesen Vorgang für $o_2$ wiederholen (und uns daran erinnern, dass das Ziel 0.99) erhalten wir:

$E_{o2} = 0.023560026$

Der Gesamtfehler für das neuronale Netz ist die Summe dieser Fehler:

$E_{Gesamt} = E_{o1} + E_{o2} = 0,274811083 + 0,023560026 = 0,298371109$

Der Rückwärtsdurchlauf

Unser Ziel bei der Backpropagation ist es, jedes der Gewichte im Netzwerk so zu aktualisieren, dass sie die tatsächliche Ausgabe näher an die Zielausgabe heranführen, wodurch der Fehler für jedes Ausgangsneuron und das Netzwerk als Ganzes minimiert wird.

Output Layer

Betrachten Sie $w_5$ . Wir wollen wissen, wie stark sich eine Änderung von $w_5$ auf den Gesamtfehler auswirkt, also $\frac{\partial E_{total}}{\partial w_{5}}$ .

$\frac{\partial E_{total}}{\partial w_{5}}$ wird gelesen als „die partielle Ableitung von $E_{total}$ nach $w_{5}$ „. Man kann auch sagen „die Steigung in Bezug auf $w_{5}$ „.

Durch Anwendung der Kettenregel wissen wir, dass:

$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$

Visuell gesehen, machen wir Folgendes:

output_1_backprop (4)

Wir müssen jeden Teil in dieser Gleichung herausfinden.

Erstens, wie stark ändert sich der Gesamtfehler in Bezug auf die Ausgabe?

$E_{Gesamt} = \frac{1}{2}(target_{o1} - out_{o1})^{2} + \frac{1}{2}(target_{o2} - out_{o2})^{2}$

$\frac{\partial E_{total}}{\partial out_{o1}} = 2 * \frac{1}{2}(target_{o1} - out_{o1})^{2 - 1} * -1 + 0$

$\frac{\partial E_{total}}{\partial out_{o1}} = -(target_{o1} - out_{o1}) = -(0,01 - 0,75136507) = 0.74136507$

$-(Ziel - out)$ wird manchmal ausgedrückt als $out - Ziel$

Wenn wir die partielle Ableitung des Gesamtfehlers nach $out_{o1}$ nehmen, wird die Größe $\frac{1}{2}(target_{o2} - out_{o2})^{2}$ Null, weil $out_{o1}$ sie nicht beeinflusst, was bedeutet, dass wir die Ableitung einer Konstanten nehmen, die Null ist.

Nächste Frage: Wie stark ändert sich der Ausgang von $o_1$ in Bezug auf seinen gesamten Nettoeingang?

Die partielle Ableitung der logistischen Funktion ist der Output multipliziert mit 1 minus dem Output:

$out_{o1} = \frac{1}{1+e^{-net_{o1}}$

$\frac{\partial out_{o1}}{\partial net_{o1}} = out_{o1}(1 - out_{o1}) = 0.75136507(1 - 0.75136507) = 0.186815602$

Schließlich, wie stark ändert sich der gesamte Netto-Input von $o1$ in Bezug auf $w_5$ ?

$net_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1$

$\frac{\partial net_{o1}}{\partial w_{5}} = 1 * out_{h1} * w_5^{(1 - 1)} + 0 + 0 = out_{h1} = 0.593269992$

Alles zusammenfassen:

$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$

$\frac{\partial E_{total}}{\partial w_{5}} = 0.74136507 * 0.186815602 * 0.593269992 = 0.082167041$

Sie werden diese Berechnung oft in Form der Delta-Regel kombiniert sehen:

$\frac{\partial E_{total}}{\partial w_{5}} = -(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1}) * out_{h1}$

Alternativ, haben wir $\frac{\partial E_{total}}{\partial out_{o1}}$ und $\frac{\partial out_{o1}}{\partial net_{o1}}$ , was als $\frac{\partial E_{total}}{\partial net_{o1}}$ geschrieben werden kann, auch bekannt als $\delta_{o1}$ (der griechische Buchstabe delta), auch bekannt als das Knoten-Delta. Wir können dies verwenden, um die obige Berechnung umzuschreiben:

$\delta_{o1} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} = \frac{\partial E_{total}}{\partial net_{o1}}$

$\delta_{o1} = -(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1})$

Daraus folgt:

$\frac{\partial E_{total}}{\partial w_{5}} = \delta_{o1} out_{h1}$

Einige Quellen extrahieren das negative Vorzeichen aus $\delta$ , so dass es geschrieben werden würde als:

$\frac{\partial E_{total}}{\partial w_{5}} = -\delta_{o1} out_{h1}$

Um den Fehler zu verringern, subtrahieren wir dann diesen Wert von der aktuellen Gewichtung (optional multipliziert mit einer Lernrate, eta, die wir auf 0 setzen werden.5):

$w_5^{+} = w_5 - \eta * \frac{\partial E_{total}}{\partial w_{5}} = 0.4 - 0.5 * 0.082167041 = 0.35891648$

Einige Quellen verwenden $\alpha$ (alpha), um die Lernrate darzustellen, andere verwenden $\eta$ (eta), und wieder andere verwenden sogar $\epsilon$ (epsilon).

Wir können diesen Vorgang wiederholen, um die neuen Gewichte $w_6$ $w_7$ , und $w_8$ zu erhalten:

$w_6^{+} = 0.408666186$

$w_7^{+} = 0.511301270$

$w_8^{+} = 0.561370121$

Wir führen die eigentlichen Aktualisierungen im neuronalen Netz durch, nachdem wir die neuen Gewichte haben, die in die Neuronen der versteckten Schicht führen (d. h., wir verwenden die ursprünglichen Gewichte, nicht die aktualisierten Gewichte, wenn wir unten mit dem Backpropagation-Algorithmus fortfahren).

Hintere Schicht

Als Nächstes setzen wir den Rückwärtsdurchlauf fort, indem wir neue Werte für $w_1$ berechnen, $w_2$ $w_3$ , und $w_4$ .

Im Großen und Ganzen müssen wir folgendes herausfinden:

$\frac{\partial E_{total}}{\partial w_{1}} = \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

Visuell:

nn-Berechnung

Wir werden ein ähnliches Verfahren wie für die Ausgabeschicht verwenden, aber etwas anders, um der Tatsache Rechnung zu tragen, dass die Ausgabe jedes Neurons der versteckten Schicht zur Ausgabe (und damit zum Fehler) mehrerer Ausgangsneuronen beiträgt. Wir wissen, dass $out_{h1}$ sowohl $out_{o1}$ als auch $out_{o2}$ beeinflusst. muss das $\frac{\partial E_{total}}{\partial out_{h1}}$ seine Wirkung auf die beiden Ausgangsneuronen berücksichtigen:

$\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}}$

Beginnend mit $\frac{\partial E_{o1}}{\partial out_{h1}}$ :

$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}$

Wir können $\frac{\partial E_{o1}}{\partial net_{o1}}$ mit den Werten berechnen, die wir zuvor berechnet haben:

$\frac{\partial E_{o1}}{\partial net_{o1}} = \frac{\partial E_{o1}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} = 0,74136507 * 0,186815602 = 0.138498562$

Und $\frac{\partial net_{o1}}{\partial out_{h1}}$ ist gleich $w_5$ :

$net_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1$

$\frac{\partial net_{o1}}{\partial out_{h1}} = w_5 = 0.40$

Einstecken:

$\frac{\partial E_{o1}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}} = 0.138498562 * 0.40 = 0.055399425$

Wenn wir den gleichen Prozess für $\frac{\partial E_{o2}}{\partial out_{h1}}$ verfolgen, erhalten wir:

$\frac{\partial E_{o2}}{\partial out_{h1}} = -0.019049119$

Daher:

$\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}} = 0,055399425 + -0,019049119 = 0.036350306$

Nun, da wir $\frac{\partial E_{total}}{\partial out_{h1}}$ haben, müssen wir $\frac{\partial out_{h1}}{\partial net_{h1}}$ herausfinden und dann $\frac{\partial net_{h1}}{\partial w}$ für jedes Gewicht:

$out_{h1} = \frac{1}{1+e^{-net_{h1}}$

$\frac{\partial out_{h1}}{\partial net_{h1}} = out_{h1}(1 - out_{h1}) = 0.59326999(1 - 0.59326999 ) = 0.241300709$

Wir berechnen die partielle Ableitung des gesamten Netzeingangs für $h_1$ nach $w_1$ genauso wie für das Ausgangsneuron:

$net_{h1} = w_1 * i_1 + w_3 * i_2 + b_1 * 1$

$\frac{\partial net_{h1}}{\partial w_1} = i_1 = 0.05$

Zusammengefasst:

$\frac{\partial E_{total}}{\partial w_{1}} = \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial w_{1}} = 0.036350306 * 0.241300709 * 0.05 = 0.000438568$

Sie könnten dies auch geschrieben sehen als:

$\frac{\partial E_{total}}{\partial w_{1}} = (\sum\limits_{o}{\frac{\partial E_{total}}{\partial out_{o}} * \frac{\partial out_{o}}{\partial net_{o}} * \frac{\partial net_{o}}{\partial out_{h1}}) * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial w_{1}} = (\sum\limits_{o}{\delta_{o} * w_{ho}}) * out_{h1}(1 - out_{h1}) * i_{1}$

$\frac{\partial E_{total}}{\partial w_{1}} = \delta_{h1}i_{1}$

Wir können nun $w_1$ aktualisieren:

$w_1^{+} = w_1 - \eta * \frac{\partial E_{total}}{\partial w_{1}} = 0.15 - 0.5 * 0.000438568 = 0.149780716$

Wiederhole dies für $w_2$ $w_3$ und $w_4$

$w_2^{+} = 0.19956143$

$w_3^{+} = 0.24975114$

$w_4^{+} = 0.29950229$

Zuletzt haben wir alle unsere Gewichte aktualisiert! Als wir ursprünglich die 0,05- und 0,1-Eingänge weiterleiteten, betrug der Fehler des Netzwerks 0,298371109. Nach dieser ersten Runde der Backpropagation ist der Gesamtfehler jetzt auf 0,291027924 gesunken. Das mag nicht viel erscheinen, aber nachdem dieser Prozess beispielsweise 10.000 Mal wiederholt wurde, sinkt der Fehler auf 0,0000351085. An diesem Punkt, wenn wir 0,05 und 0,1 vorwärts einspeisen, erzeugen die beiden Ausgänge Neuronen 0,015912196 (gegenüber dem 0,01-Ziel) und 0,984065734 (gegenüber dem 0,99-Ziel).

Wenn Sie es bis hierher geschafft haben und irgendwelche Fehler in den obigen Ausführungen gefunden haben oder Ihnen eine Möglichkeit einfällt, es für zukünftige Leser klarer zu machen, zögern Sie nicht, mir eine Nachricht zu schicken. Danke!