Hintergrund
Elliptic Curve Cryptography (ECC) ist ein Ansatz zur Public-Key-Kryptographie, der auf der algebraischen Struktur von elliptischen Kurven über endlichen Feldern basiert. ECC erfordert einen kleineren Schlüssel im Vergleich zur Nicht-ECC-Kryptografie, um eine gleichwertige Sicherheit zu bieten (eine 256-Bit-ECC-Sicherheit hat eine gleichwertige Sicherheit, die von einer 3072-Bit-RSA-Kryptografie erreicht wird).
Für ein besseres Verständnis der Elliptischen Kurven-Kryptografie ist es sehr wichtig, die Grundlagen der Elliptischen Kurve zu verstehen. Eine elliptische Kurve ist eine planare algebraische Kurve, die durch eine Gleichung der Form
![]()
Wobei ‚a‘ der Koeffizient von x und ‚b‘ die Konstante der Gleichung ist
Die Kurve ist nichtsingulär; d.h. ihr Graph hat keine Scheitelpunkte oder Selbstschnittpunkte (wenn die Charakteristik des Koeffizientenfeldes gleich 2 oder 3 ist).
Im Allgemeinen sieht eine elliptische Kurve wie unten dargestellt aus. Elliptische Kurven können sich in fast 3 Punkten schneiden, wenn eine gerade Linie gezogen wird, die die Kurve schneidet. Wie wir sehen können, ist die elliptische Kurve symmetrisch um die x-Achse, diese Eigenschaft spielt eine Schlüsselrolle im Algorithmus.
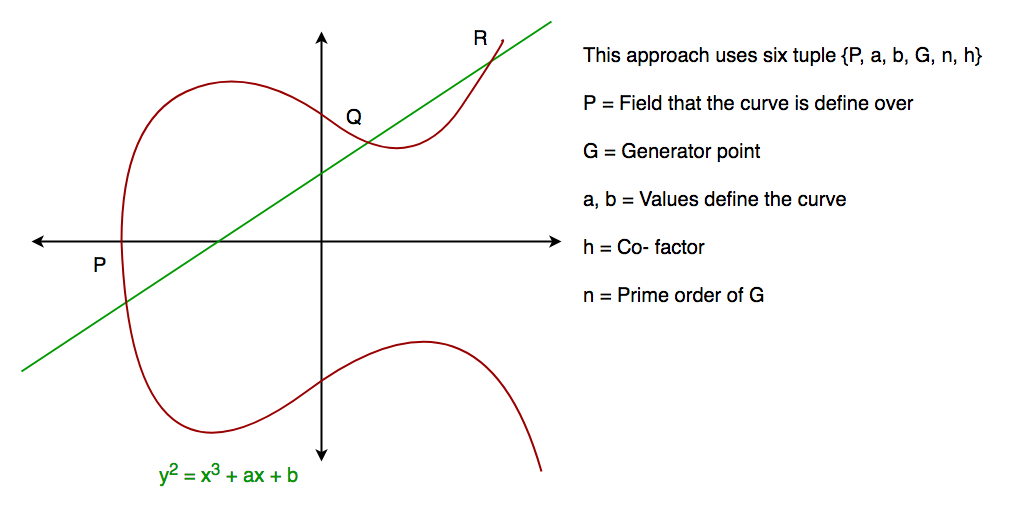
Diffie-Hellman-Algorithmus
Der Diffie-Hellman-Algorithmus wird verwendet, um ein gemeinsames Geheimnis zu etablieren, das für die geheime Kommunikation beim Austausch von Daten über ein öffentliches Netzwerk verwendet werden kann, indem die elliptische Kurve verwendet wird, um Punkte zu generieren und den geheimen Schlüssel anhand der Parameter zu erhalten.
- Der Einfachheit halber und zur praktischen Umsetzung des Algorithmus betrachten wir nur 4 Variablen, eine Primzahl P und G (eine primitive Wurzel aus P) und zwei private Werte a und b.
- P und G sind beides öffentlich verfügbare Zahlen. Die Benutzer (sagen wir Alice und Bob) wählen die privaten Werte a und b und generieren einen Schlüssel und tauschen ihn öffentlich aus, die andere Person erhält den Schlüssel und generiert daraus einen geheimen Schlüssel, nach dem sie den gleichen geheimen Schlüssel zum Verschlüsseln haben.
Schrittweise Erläuterung
| Alice | Bob |
|---|---|
| Public Keys available = P, G | Öffentliche Tasten verfügbar = P, G |
| Privater Schlüssel ausgewählt = a | Privater Schlüssel ausgewählt = b |
|
Schlüssel erzeugt =
|
Schlüssel erzeugt =
|
| Austausch der generierten Schlüssel findet statt | |
| Schlüssel erhalten = y | Schlüssel erhalten = x |
|
Generierter geheimer Schlüssel =
|
Generierter geheimer Schlüssel =
|
|
Algebraisch kann gezeigt werden, dass
|
|
| Der Anwender hat nun einen symmetrischen geheimen Schlüssel zum Verschlüsseln | |
Beispiel
Step 1: Alice and Bob get public numbers P = 23, G = 9Step 2: Alice selected a private key a = 4 and Bob selected a private key b = 3Step 3: Alice and Bob compute public valuesAlice: x =(9^4 mod 23) = (6561 mod 23) = 6 Bob: y = (9^3 mod 23) = (729 mod 23) = 16Step 4: Alice and Bob exchange public numbersStep 5: Alice receives public key y =16 and Bob receives public key x = 6Step 6: Alice and Bob compute symmetric keys Alice: ka = y^a mod p = 65536 mod 23 = 9 Bob: kb = x^b mod p = 216 mod 23 = 9Step 7: 9 is the shared secret.
Implementierung:
#include<stdio.h>#include<math.h>longlongintpower(longlonginta, longlongintb, longlongintP) { if(b == 1) returna; else return(((longlongint)pow(a, b)) % P); }intmain() { longlongintP, G, x, a, y, b, ka, kb;
P = 23; printf("The value of P : %lld\n", P); G = 9; printf("The value of G : %lld\n\n", G); a = 4; printf("The private key a for Alice : %lld\n", a); x = power(G, a, P); b = 3; printf("The private key b for Bob : %lld\n\n", b); y = power(G, b, P); ka = power(y, a, P); kb = power(x, b, P); printf("Secret key for the Alice is : %lld\n", ka); printf("Secret Key for the Bob is : %lld\n", kb); return0; }
fromrandom importrandint if__name__ =='__main__':
P =23 G =9 print('The Value of P is :%d'%(P)) print('The Value of G is :%d'%(G))
a =4 print('The Private Key a for Alice is :%d'%(a)) x =int(pow(G,a,P)) b =3 print('The Private Key b for Bob is :%d'%(b))
y =int(pow(G,b,P)) ka =int(pow(y,a,P))
kb =int(pow(x,b,P)) print('Secret key for the Alice is : %d'%(ka)) print('Secret Key for the Bob is : %d'%(kb))
Ausgabe
The value of P : 23The value of G : 9The private key a for Alice : 4The private key b for Bob : 3Secret key for the Alice is : 9Secret Key for the Bob is : 9
Dieser Artikel wurde von Souvik Nandi verfasst. Wenn Ihnen GeeksforGeeks gefällt und Sie einen Beitrag leisten möchten, können Sie auch einen Artikel über contribute.GeeksforGeeks.org schreiben oder eine Mail an [email protected] schicken. Sehen Sie, wie Ihr Artikel auf der GeeksforGeeks-Hauptseite erscheint, und helfen Sie anderen Geeks.
Bitte schreiben Sie Kommentare, wenn Sie etwas falsch finden oder weitere Informationen zu dem oben besprochenen Thema mitteilen möchten.