Familienweise Fehlerraten > Holm-.Bonferroni-Methode

Vielleicht möchten Sie zuerst diesen Artikel lesen: Familienweise Fehlerraten.

Was ist die Holm-Bonferroni-Methode?

Die Holm-Bonferroni-Methode (auch Holm’s Sequential Bonferroni Procedure genannt) ist eine Möglichkeit, mit familienweisen Fehlerraten (FWER) für multiple Hypothesentests umzugehen. Sie ist eine Modifikation der Bonferroni-Korrektur. Die Bonferroni-Korrektur reduziert die Möglichkeit eines statistisch signifikanten Ergebnisses (d. h. eines Fehlers vom Typ I), wenn mehrere Tests durchgeführt werden. Obwohl die Bonferroni-Korrektur einfach zu berechnen ist, leidet sie unter einem Mangel an statistischer Aussagekraft. Die Holm-Bonferroni-Methode ist ebenfalls recht einfach zu berechnen, aber sie ist leistungsfähiger als die einstufige Bonferroni-Methode.

Formel

Die Formel zur Berechnung der Holm-Bonferroni-Methode lautet: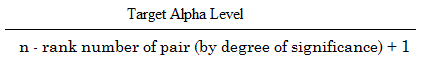

Wobei:

• Ziel-Alpha-Niveau = Gesamt-Alpha-Niveau (normalerweise .05),
• n = Anzahl der Tests.

Das nächste Beispiel zeigt, wie die Formel funktioniert.

Beispiel

Frage: Testen Sie mit der Holm-Bonferroni-Methode die folgenden vier Hypothesen und ihre zugehörigen p-Werte bei einem Alpha-Niveau von .05:

• H1 = 0.01.
• H2 = 0.04
• H3 = 0.03
• H4 = 0.005

Hinweis: Wir kennen bereits die p-Werte, die mit jeder Hypothese verbunden sind. Wenn Sie die p-Werte nicht kennen, führen Sie einen Test für jede Hypothese durch, bevor Sie versuchen, FWER mit der Holm-Bonferroni-Methode anzupassen.

Schritt 1: Ordnen Sie die p-Werte vom kleinsten zum größten Wert:

• H4 = 0.005
• H1 = 0,01
• H3 = 0,03
• H2 = 0,04

Schritt 2: Arbeiten Sie die Holm-Bonferroni-Formel für den ersten Rang:
HB = Ziel α / (n – Rang + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Schritt 3: Vergleichen Sie den erstrangigen (kleinsten) p-Wert aus Schritt 1 mit dem in Schritt 2 berechneten Alpha-Niveau:
Kleinster p-Wert, in Schritt 1 (H4 = 0.005) <Alpha-Niveau in Schritt 2 (.0125).
Wenn der p-Wert kleiner ist, verwerfen Sie die Nullhypothese für diesen Einzeltest.

Der p-Wert von .005 ist kleiner als .0125, also wird die Nullhypothese für H4 abgelehnt.

Schritt 4: Wiederholen Sie die HB-Formel für den zweiten Rang .
HB = Ziel α / (n – Rang + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

Schritt 5: Vergleichen Sie das Ergebnis aus der HB-Formel in Schritt 4 mit dem p-Wert des zweiten Ranges:
Zweitrangiger p-Wert, in Schritt 1 (H1 = 0,01) < Alpha-Niveau in Schritt 2 (.0167).
Der p-Wert von .01 ist kleiner als .0167, also wird auch die Nullhypothese für H1 abgelehnt.

Schritt 6: Wiederholen Sie die HB-Formel für den dritten Rang.
HB = Ziel α / (n – Rang + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

Schritt 7: Vergleichen Sie das Ergebnis aus der HB-Formel in Schritt 6 mit dem p-Wert des dritten Ranges:
Drittrangiger p-Wert, in Schritt 1 (H3 = 0,03) > Alpha-Niveau in Schritt 6 (.025).
Der p-Wert von .03 ist größer als .025, also wird die Nullhypothese für H3 nicht abgelehnt.

Der Test stoppt, wenn Sie die erste nicht abgelehnte Hypothese erreichen. Alle nachfolgenden Hypothesen sind nicht signifikant (d.h. nicht abgelehnt).

Referenz:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf dem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!