Einführung

Das Säulenknicken ist ein interessantes und einzigartiges Thema. Es ist vielleicht der einzige Bereich der Strukturmechanik, in dem das Versagen nicht mit der Festigkeit des Materials zusammenhängt. Eine Stützenknickanalyse besteht darin, die maximale Last zu bestimmen, die eine Stütze tragen kann, bevor sie zusammenbricht. Aber bei langen Stützen hat der Zusammenbruch nichts mit der Materialnachgiebigkeit zu tun. Auf dieser Seite werden die Standardgleichungen für das Knicken von Stützen mit zwei Ansätzen hergeleitet: Zunächst wird die übliche Entwicklung der Gleichungen behandelt, d.h. die Eulersche Knickungstheorie. Dies ist die Ableitung, die in Lehrbüchern zu finden ist und in Ingenieurkursen vorgestellt wird. Aber ich habe sie nie gemocht. Nicht, weil sie falsch ist (sie ist richtig), sondern weil ich denke, dass sie die physikalischen Mechanismen, die den Knickprozess bestimmen, nicht zufriedenstellend darstellt. Deshalb wird auch eine zweite Ableitung der Knickgleichungen vorgestellt.
Kurioserweise werden Objekte als Stützen bezeichnet, wenn sie axial auf Druck belastet werden, wie es hier der Fall ist, aber sie werden als Balken bezeichnet, wenn sie quer belastet werden.
Nichtsdestotrotz ist die Balkenbiegetheorie von zentraler Bedeutung für Stützenknickanalysen, deshalb wird dem Leser empfohlen, diese Balkenbiegeseite zu lesen.
Eulersche Knickungstheorie
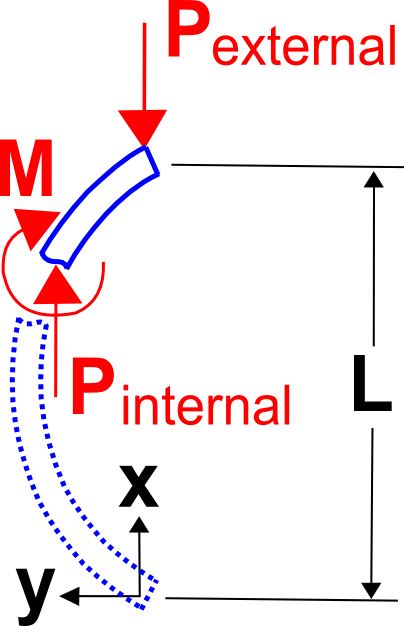
Die Eulersche Knickungstheorie ist die klassische Theorie, die in Lehrbüchern und Klassenzimmern vorgestellt wird. Sie beginnt einfach mit der Feststellung, dass das innere Biegemoment in einer belasteten und verformten Stütze \(-P \, y\) ist, wobei \(P \) die Druckbelastung und \(y\) die Durchbiegung der Stütze ist. Setzen Sie also \(-P \, y\) für \(M\) in die Balkenbiegegleichung ein, \( E \, I \, y“ = M \).
\
Daraus ergibt sich die folgende Differentialgleichung
\
, die die Lösung
\
hat, wobei \(A\) und \(B\) Konstanten sind, die aus den Randbedingungen bestimmt werden.
Die Randbedingungen sind \(y = 0\) bei \(x = 0\) und \(x = L\).
Die erste Randbedingung, \(y = 0\) bei \(x = 0\), führt zu dem Schluss, dass \(B = 0\). Und damit bleibt
\
So weit, so gut. Aber an diesem Punkt neigt die klassische Herleitung dazu, die physikalische Intuition hinter sich zu lassen und offenkundig mathematisch zu werden…
Die Sache wird mit der zweiten Randbedingung sehr interessant, weil sie, wie wir sehen werden, nicht zur Bestimmung der unbekannten Konstante \(A\) führt. Um dies zu sehen, fügen Sie die zweite Randbedingung wie folgt ein.
Hier gibt es grundsätzlich zwei Möglichkeiten. Im ersten Fall ist \(A = 0\), aber das ist langweilig, weil es zu dem Ergebnis führt, dass alle Verschiebungen null sind. Dies ist nur die nicht geknickte Lösung. Bevor die Säule knickt, sind ihre seitlichen Verschiebungen einfach null.
Der zweite Fall ist der interessante und der, der direkt mit dem Knicken der Säule zusammenhängt. Die zweite Methode, die Randbedingung zu erfüllen, besteht darin, zu beachten, dass \(\sin(\pi) = 0\). Daher ist der Weg, die Randbedingung zu erfüllen, zu verlangen, dass das Argument in der Gleichung, \(\left( \sqrt{{P \over E \, I}} \; L \right)\) gleich \(\pi\) sein muss.Dies ergibt
\
und die Lösung für \(P\) ergibt
\
Dies ist das klassische Ergebnis der Eulerschen Knickungstheorie. Es gibt den kritischen Wert der Last \(P\), genannt \(P_{cr}\), oberhalb dessen die Säule knickt.
Dieses Ergebnis ist vollkommen legitim. Allerdings ist es, wie inzwischen klar sein sollte, sehr mathematisch und liefert daher wenig physikalische Erkenntnisse. In der folgenden Ableitung wird eine alternative Methode vorgestellt, um zur gleichen Gleichung zu gelangen, die meines Erachtens einen viel direkteren physikalischen Zusammenhang mit dem Knickvorgang herstellt als die obige Ableitung.

Knicken vs. Fließen
Wie eingangs erwähnt, ist die klassische Knickanalyse unabhängig von der Fließgrenze eines Materials. Dies wird in der obigen Herleitung deutlich, da zu keinem Zeitpunkt Spannung oder Dehnung diskutiert oder mit der Festigkeit eines Materials verglichen wurde.
Aber in der Tat sollten Überlegungen zur Fließfähigkeit nie völlig ignoriert werden. Sobald man eine Schätzung von P_{cr}} aus der obigen Gleichung erhalten hat, sollte man sie immer durch die Querschnittsfläche der Säule dividieren, um eine Spannung
\
zu erhalten und diesen Wert mit der Streckgrenze des Materials zu vergleichen, um festzustellen, ob ein Fließen vor dem Knicken auftritt. Dies ist für kurze Stützen kritisch, da sie von Natur aus hohe \(P_{cr}\) Werte haben, da \(L^2\) im Nenner der Knickgleichung steht.

Endzwänge beim Knicken
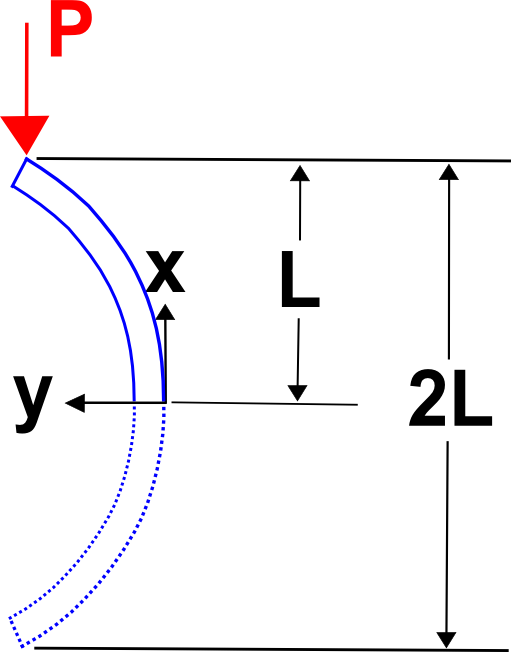
Obwohl es nicht der Schwerpunkt dieser Seite ist, ist es wichtig zu erkennen, dass Endzwangsbedingungen für Knickanalysen kritisch sind, da sie den Wert von \(P_{cr}\) verändern. Betrachten Sie zum Beispiel, dass die kritische Knicklast der hier gezeigten Säule durch
\
gegeben ist. Beachten Sie, dass dieser Wert 1/4 des Wertes ist, der in der früheren Gleichung für \(P_{cr}\) angegeben wurde. Die Skizze zeigt, dass die Knickbedingung hier genau äquivalent zum Knicken einer doppelt so langen Säule mit den gleichen Randbedingungen wie in der obigen Ableitung ist. Und dies führt zu
\
Physikalisch basierte Knickableitung
In diesem Abschnitt wird eine alternative Methode zur Bestimmung kritischer Knicklasten vorgestellt, die meiner Meinung nach physikalisch intuitiver ist als die klassische Eulersche Knicktheorie. Ihr Hauptmerkmal ist der Vergleich des inneren Biegemoments, das sich aus der inneren Spannungsverteilung ergibt, mit dem äußeren Biegemoment, das sich aus der auf die Stütze wirkenden Last ergibt. (Der vorige Satz ist kritisch.)
Dieser Ansatz setzt ungefähr dort an, wo zuvor festgestellt wurde, dass der klassische Euler-Ansatz zu mathematisch wird. Der erste Schritt besteht darin, eine verformte Form anzunehmen. Wir wissen, dass \(y = 0\) an beiden Enden der Säule ist und dass die Form einer \(\sin()\)-Funktion folgt, die auf der oben genannten Differentialgleichung beruht. Die logischste Wahl ist also
\
, wobei \(\delta_{max}\) die seitliche Verschiebung in der Mitte der Säule ist. Ihr Wert ist unbekannt, aber es ist bekannt, dass sie am Mittelpunkt größer ist als an jedem anderen Punkt der Säule, daher der tiefgestellte Index \(max\). Die Wahl von \(\pi x / L\) als Argument der Funktion \(\sin()\) stellt sicher, dass die Verschiebungen bei \(x = 0\) und \(x = L\) null sind. (Wir werden in Kürze über andere angenommene Formen sprechen.)

Wenn Sie sich über den Term \(\sqrt{P/EI}\) in der Funktion \(\sin()\) aus der früheren Euler-Lösung wundern, lassen Sie es. Er ergab sich aus der Lösung der Differentialgleichung, aber wir tun hier so, als wüssten wir nichts über die Details dieser Lösung (Ausnahmealarm!).Wir brauchen nur eine Funktion, die einer gekrümmten Säule mit Nullverschiebungen an ihren Enden ähneln kann. Die Verwendung von \(\sin ( {\pi x \over L} )\) erreicht dies.
Der „Ausnahmealarm“ ist oben vorhanden, weil wir in der Tat ein Stück Wissen über die frühere Analyse ausnutzen. Daher sollten Sinus und Kosinus, wann immer möglich, zur Beschreibung der verformten Formen verwendet werden, da sie zu den genauesten Schätzungen von \(P_{cr}\) führen.
Erinnern Sie sich aus der Balkenbiegetheorie, dass das Biegemoment, \(M\), mit der Durchbiegung der Stütze durch
\
zusammenhängt. Obwohl nicht kritisch, ist es hilfreich, sich daran zu erinnern, dass diese Beziehung aus der Berechnung des Moments im Querschnitt aufgrund der Spannungsverteilung stammt. Die Beziehung zeigt, dass wir die zweite Ableitung der angenommenen Verschiebungsfunktion benötigen.
\
Dies ist das innere Biegemoment in der Stütze aufgrund der Spannungsverteilung in ihr, die wiederum auf die Tatsache zurückzuführen ist, dass die Stütze gebogen ist.
Hier kommt ein wichtiger Gedanke… Dieses Biegemoment kann man sich als den inneren Biegewiderstand der Stütze vorstellen, also die Kraft, mit der sie versucht, sich wieder aufzurichten.
Der einfache nächste Schritt ist, dieses innere Widerstandsbiegemoment mit dem aus der äußeren Belastung resultierenden gleichzusetzen. Dieser Betrag ist einfach
(M = -P \, y(x)\). Die Gleichsetzung der beiden ergibt
\
Es ist an dieser Stelle nicht schwer zu erkennen, dass dieser Ansatz zum gleichen Ausdruck für \(P_{cr}\) führt wie die klassische Eulersche Knicktheorie.
Aber auf dem Weg dorthin hat er viel mehr Einblick in den physikalischen Prozess des Knickens geliefert als die frühere Theorie. Nämlich…
- Wir sind zu dieser Beziehung gelangt, indem wir das innere Biegemoment (aufgrund der inneren Spannungen, die aus der Biegung der Säule resultieren) mit dem äußeren Biegemoment gleichgesetzt haben, das aus der äußeren Last resultiert, \(P\).Es sollte klar sein, dass Knicken auftritt, wenn \(P\) groß genug ist, um die Gleichung zu erfüllen.
- Die Tatsache, dass \(y(x)\) auf beiden Seiten der Gleichung auftaucht und sich daher aufhebt, bedeutet, dass das Knicken, wenn es auftritt, gleichzeitig über die gesamte Länge der Säule erfolgt. (Ein faszinierendes Ergebnis, das in der Euler-Theorie nicht ersichtlich ist.)
Wie auch immer, das Streichen von \(y(x)\) aus beiden Seiten der Gleichung ergibt
\
wieder, aber diesmal mit viel mehr physikalischer Einsicht.

Beispiel mit festem Ende
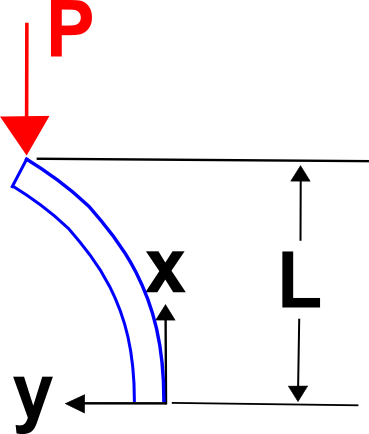
Nehmen Sie diesmal eine verformte Form an
\
Berechnen Sie das dadurch entstehende Biegemoment.
\
Das Biegemoment infolge der äußeren Belastung ist \(M = P ( \delta_{max} – y(x) )\). Durch Gleichsetzen und Vereinfachen erhält man das bekannte Ergebnis.
\

Beispiel mit festem Ende und anderer angenommener Form
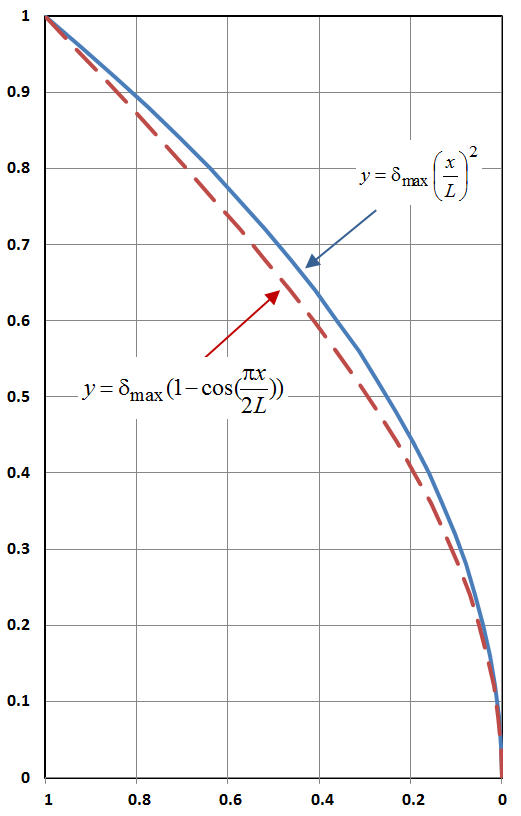
Dieses Beispiel soll zeigen, dass für die verformte Form der Stütze alternative Funktionen angenommen werden können, und dass die resultierende Formel für \(P_{cr}\) sich nicht wesentlich von der exakten Lösung unterscheidet.
Nehmen Sie diesmal eine verformte Form von
Berechnen Sie das daraus resultierende Biegemoment.
\
Das Biegemoment aufgrund der äußeren Last bleibt \(M = P ( \delta_{max} – y(x) )\). Die Gleichsetzung dieser beiden ergibt
\
Aus der Gleichung geht klar hervor, dass der Minimalwert von \(P\) bei \(x = 0\) auftritt, da an diesem Punkt \(y(x)\) ein Minimum ist (genau genommen Null) und daher \((\delta_{max} – y(x))\) ein Maximum ist. Setzt man \(y(x)\) auf Null und streicht \(\delta_{max}\) von beiden Seiten, so erhält man
\
Dieses Ergebnis ist natürlich nicht gleich der exakten Lösung oben. Der Unterschied besteht darin, dass die exakte Lösung \(\pi^2 / 4 = 2,467\) enthält, während diese Näherungslösung 2 enthält, ein Unterschied von 23 %. Signifikant, aber nicht so groß wie, sagen wir, ein Faktor von 2 oder eine Größenordnung. Beachten Sie auch, dass die Näherungslösung konservativ ist, da sie eine kritische Knicklast ergibt, die geringer ist als die der exakten Lösung.
Interessant ist, dass diese Lösung, die auf der quadratischen Form basiert, zu einer niedrigeren kritischen Knicklast und einer Konzentration des Knickversagens an der Basis der Säule führt.Im Gegensatz dazu führte die exakte Lösung, die aus der trigonometrischen Funktion besteht, zu einer gleichmäßigen Knickneigung über die gesamte Länge der Stütze und zu einem entsprechend höheren \(P_{cr}\).
Ein Schlüsselfaktor ist hier, dass die angenommene quadratische verformte Form keine exakte Lösung der herrschenden Differentialgleichung ist (obwohl sie nahe dran ist). Trigonometrische Funktionen schon.