Dies ist ein Vektor:

Ein Vektor hat Betrag (Größe) und Richtung:
Die Länge der Linie gibt den Betrag an und die Pfeilspitze zeigt in die Richtung.
Wir können zwei Vektoren addieren, indem wir sie Kopf an Kopf verbinden:
Und es ist egal, in welcher Reihenfolge wir sie addieren, wir erhalten das gleiche Ergebnis:
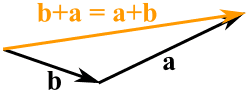
Beispiel: Ein Flugzeug fliegt entlang, zeigt nach Norden, aber es weht ein Wind aus Nordwest.
Die beiden Vektoren (die Geschwindigkeit, die durch den Propeller verursacht wird, und die Geschwindigkeit des Windes) führen zu einer etwas langsameren Geschwindigkeit über Grund, die etwas östlich von Norden liegt.
Wenn Sie das Flugzeug vom Boden aus beobachten würden, würde es den Anschein erwecken, dass es ein wenig seitwärts rutscht.
Haben Sie das schon einmal gesehen? Vielleicht haben Sie Vögel gesehen, die gegen einen starken Wind ankämpfen und seitwärts zu fliegen scheinen. Vektoren helfen, das zu erklären.
Geschwindigkeit, Beschleunigung, Kraft und viele andere Dinge sind Vektoren.
Subtrahieren
Wir können auch einen Vektor von einem anderen subtrahieren:
- Zuerst kehren wir die Richtung des Vektors um, den wir subtrahieren wollen,
- dann addieren wir sie wie gewohnt:
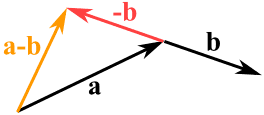
a – b
Notation
Ein Vektor wird oft fett geschrieben, wie a oder b.
| Ein Vektor kann auch als die Buchstaben seines Kopfes und seines Endes mit einem Pfeil darüber geschrieben werden, etwa so: |
 |
Berechnungen
Nun …. wie machen wir die Berechnungen?
Am häufigsten werden Vektoren zunächst in x- und y-Anteile zerlegt, etwa so:
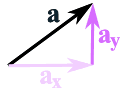
Der Vektor a wird zerlegt in
die beiden Vektoren ax und ay
(Wie das geht, sehen wir später.)
Vektoren addieren
Wir können dann Vektoren addieren, indem wir die x-Teile addieren und die y-Teile addieren:
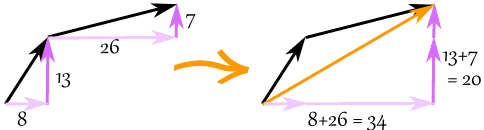
Der Vektor (8, 13) und der Vektor (26, 7) addieren sich zum Vektor (34, 20)
Beispiel: Addiere die Vektoren a = (8, 13) und b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Wenn wir einen Vektor auf diese Weise zerlegen, nennt man jeden Teil eine Komponente:
Vektoren subtrahieren
Um zu subtrahieren, kehren wir zuerst den Vektor um, den wir subtrahieren wollen, und addieren dann.
Beispiel: Subtrahiere k = (4, 5) von v = (12, 2)
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
Magnitude eines Vektors
Die Magnitude eines Vektors wird durch zwei senkrechte Balken auf beiden Seiten des Vektors dargestellt:
|a|
Oder er kann mit zwei senkrechten Balken geschrieben werden (um ihn nicht mit dem Absolutwert zu verwechseln):
|a||
Wir berechnen ihn mit dem Satz des Pythagoras:
a| = √( x2 + y2 )
Beispiel: Wie groß ist der Betrag des Vektors b = (6, 8) ?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Ein Vektor mit dem Betrag 1 nennt man Einheitsvektor.
Vektor vs. Skalar
Ein Skalar hat nur den Betrag (Größe).
Skalar: einfach eine Zahl (wie 7 oder -0.32) …. definitiv kein Vektor.
Ein Vektor hat Größe und Richtung und wird oft fett geschrieben, damit wir wissen, dass er kein Skalar ist:
- So ist c ein Vektor, er hat Größe und Richtung
- aber c ist nur ein Wert, wie 3 oder 12.4
Beispiel: kb ist eigentlich der Skalar k mal der Vektor b.
Multiplizieren eines Vektors mit einem Skalar
Wenn wir einen Vektor mit einem Skalar multiplizieren, nennt man das „skalieren“ eines Vektors, weil wir ändern, wie groß oder klein der Vektor ist.
Beispiel: Multiplizieren des Vektors m = (7, 3) mit dem Skalar 3
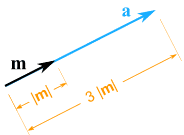 |
a = 3m = (3×7, 3×3) = (21, 9) |
Es zeigt immer noch in die gleiche Richtung, ist aber 3 mal länger
(Und jetzt wissen Sie, warum Zahlen „Skalare“ genannt werden, weil sie den Vektor nach oben oder unten „skalieren“.)
Multiplizieren eines Vektors mit einem anderen Vektor (Punktprodukt und Kreuzprodukt)
 |
Wie multipliziert man zwei Vektoren miteinander? Es gibt mehr als einen Weg!
(Lesen Sie diese Seiten für weitere Details.) |
Mehr als 2 Dimensionen
Vektoren funktionieren auch sehr gut in 3 oder mehr Dimensionen:
Der Vektor (1, 4, 5)
Beispiel: Addiere die Vektoren a = (3, 7, 4) und b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Beispiel: Wie groß ist der Betrag des Vektors w = (1, -2, 3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9) = √14
Hier ist ein Beispiel mit 4 Dimensionen (aber es ist schwer zu zeichnen!):
Beispiel: Subtrahiere (1, 2, 3, 4) von (3, 3, 3, 3)
(3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3) + (-1,-2,-3,-4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Betrag und Richtung
Wir kennen vielleicht den Betrag und die Richtung eines Vektors, wollen aber seine x- und y-Längen (oder umgekehrt):
 |
<> |  |
| Vektor a in Polar Koordinaten |
Vektor a in kartesischen Koordinaten |
Sie können unter Polare und kartesische Koordinaten nachlesen, wie man sie umrechnet, aber hier ist eine kurze Zusammenfassung:
| Von Polarkoordinaten (r,θ) zu kartesischen Koordinaten (x,y) |
Von kartesischen Koordinaten (x,y) zu Polarkoordinaten (r,θ) |
|
|---|---|---|
|
|
Ein Beispiel
Sam und Alex ziehen einen Kasten.
- Sam zieht mit einer Kraft von 200 Newton unter einem Winkel von 60°
- Alex zieht mit einer Kraft von 120 Newton unter einem Winkel von 45° wie gezeigt
Wie groß ist die kombinierte Kraft und ihre Richtung?
Lassen Sie uns die beiden Vektoren Kopf an Fuß addieren:
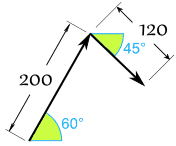
Zunächst konvertieren wir von polar zu kartesisch (auf 2 Nachkommastellen):
Sams Vektor:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0,8660 = 173.21
Alex‘ Vektor:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0,7071 = 84,85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84.85
Nun haben wir:
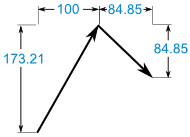
Addieren Sie:
(100, 173.21) + (84.85, -84.85) = (184.85, 88.36)
Diese Antwort ist gültig, aber konvertieren wir zurück in polar, da die Frage in polar war:
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88,36 / 184,85 ) = 25.5°
Und wir haben dieses (gerundete) Ergebnis: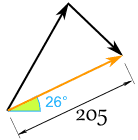
Und für Sam und Alex sieht es so aus:
Sie könnten ein besseres Ergebnis erhalten, wenn sie Schulter an Schulter stehen würden!





