Letztes Update am 25. September 2019
Anstatt die Klassenwerte für ein Klassifikationsproblem direkt vorherzusagen, kann es praktisch sein, die Wahrscheinlichkeit einer Beobachtung vorherzusagen, die zu jeder möglichen Klasse gehört.
Die Vorhersage von Wahrscheinlichkeiten ermöglicht eine gewisse Flexibilität, einschließlich der Entscheidung, wie die Wahrscheinlichkeiten zu interpretieren sind, der Darstellung von Vorhersagen mit Unsicherheiten und der Bereitstellung nuancierterer Möglichkeiten zur Bewertung der Fähigkeit des Modells.
Vorgesagte Wahrscheinlichkeiten, die der erwarteten Verteilung der Wahrscheinlichkeiten für jede Klasse entsprechen, werden als kalibriert bezeichnet. Das Problem ist, dass nicht alle Modelle für maschinelles Lernen in der Lage sind, kalibrierte Wahrscheinlichkeiten vorherzusagen.
Es gibt Methoden, um sowohl zu diagnostizieren, wie kalibriert die vorhergesagten Wahrscheinlichkeiten sind, als auch um die vorhergesagten Wahrscheinlichkeiten besser mit der beobachteten Verteilung jeder Klasse zu kalibrieren. Oft kann dies zu einer besseren Qualität der Vorhersagen führen, je nachdem, wie die Fähigkeit des Modells bewertet wird.
In diesem Lernprogramm erfahren Sie, wie wichtig die Kalibrierung der vorhergesagten Wahrscheinlichkeiten ist und wie Sie die Kalibrierung von Modellen, die für die probabilistische Klassifizierung verwendet werden, diagnostizieren und verbessern können.
Nach Abschluss dieses Tutorials wissen Sie:
- Nichtlineare Algorithmen für maschinelles Lernen sagen oft unkalibrierte Klassenwahrscheinlichkeiten voraus.
- Zuverlässigkeitsdiagramme können zur Diagnose der Kalibrierung eines Modells verwendet werden, und es können Methoden zur besseren Kalibrierung von Vorhersagen für ein Problem eingesetzt werden.
- Wie man Zuverlässigkeitsdiagramme entwickelt und Klassifikationsmodelle in Python mit scikit-learn kalibriert.
Starten Sie Ihr Projekt mit meinem neuen Buch Probability for Machine Learning, inklusive Schritt-für-Schritt-Tutorials und den Python-Quellcode-Dateien für alle Beispiele.
Lassen Sie uns loslegen.

Wie und wann man ein kalibriertes Klassifikationsmodell mit scikit-learn verwendet
Foto von Nigel Howe, einige Rechte vorbehalten.
Übersicht über das Tutorial
Dieses Tutorial ist in vier Teile unterteilt; diese sind:
- Vorhersage von Wahrscheinlichkeiten
- Kalibrierung von Vorhersagen
- Wie man Wahrscheinlichkeiten in Python kalibriert
- Arbeitsbeispiel für die Kalibrierung von SVM-Wahrscheinlichkeiten
Vorhersage von Wahrscheinlichkeiten
Ein Problem der Klassifikationsvorhersage erfordert die Vorhersage oder Prognose eines Labels für eine gegebene Beobachtung.
Alternativ zur direkten Vorhersage des Labels kann ein Modell die Wahrscheinlichkeit vorhersagen, dass eine Beobachtung zu jedem möglichen Klassenlabel gehört.
Dies bietet eine gewisse Flexibilität sowohl in der Art und Weise, wie Vorhersagen interpretiert und dargestellt werden (Wahl des Schwellenwerts und der Vorhersageunsicherheit) als auch in der Art und Weise, wie das Modell bewertet wird.
Obwohl ein Modell in der Lage ist, Wahrscheinlichkeiten vorherzusagen, stimmen die Verteilung und das Verhalten der Wahrscheinlichkeiten möglicherweise nicht mit der erwarteten Verteilung der beobachteten Wahrscheinlichkeiten in den Trainingsdaten überein.
Dies ist besonders häufig bei komplexen nichtlinearen Algorithmen für maschinelles Lernen der Fall, die keine direkten probabilistischen Vorhersagen machen und stattdessen Näherungen verwenden.
Die Verteilung der Wahrscheinlichkeiten kann angepasst werden, damit sie besser mit der in den Daten beobachteten erwarteten Verteilung übereinstimmt. Diese Anpassung wird als Kalibrierung bezeichnet, wie bei der Kalibrierung des Modells oder der Kalibrierung der Verteilung der Klassenwahrscheinlichkeiten.
Wir möchten, dass die geschätzten Klassenwahrscheinlichkeiten die wahre zugrundeliegende Wahrscheinlichkeit der Stichprobe widerspiegeln. Das heißt, die vorhergesagte Klassenwahrscheinlichkeit (oder der wahrscheinlichkeitsähnliche Wert) muss gut kalibriert sein. Um gut kalibriert zu sein, müssen die Wahrscheinlichkeiten tatsächlich die wahre Wahrscheinlichkeit des interessierenden Ereignisses widerspiegeln.
– Seite 249, Applied Predictive Modeling, 2013.
Kalibrierung von Vorhersagen
Bei der Kalibrierung von Wahrscheinlichkeiten gibt es zwei Anliegen: die Diagnose der Kalibrierung von vorhergesagten Wahrscheinlichkeiten und der Kalibrierungsprozess selbst.
Reliabilitätsdiagramme (Kalibrierungskurven)
Ein Reliabilitätsdiagramm ist ein Liniendiagramm der relativen Häufigkeit des Beobachteten (y-Achse) gegenüber der vorhergesagten Wahrscheinlichkeitshäufigkeit (x-Achse).
Reliabilitätsdiagramme sind gängige Hilfsmittel zur Veranschaulichung der Eigenschaften von probabilistischen Vorhersagesystemen. Sie bestehen aus einem Diagramm der beobachteten relativen Häufigkeit gegen die vorhergesagte Wahrscheinlichkeit und bieten einen schnellen visuellen Vergleich bei der Abstimmung probabilistischer Vorhersagesysteme sowie eine Dokumentation der Leistung des Endprodukts
– Increasing the Reliability of Reliability Diagrams, 2007.
Speziell werden die vorhergesagten Wahrscheinlichkeiten in eine feste Anzahl von Bereichen entlang der x-Achse aufgeteilt. Dann wird die Anzahl der Ereignisse (Klasse=1) für jedes Bin gezählt (z. B. die relative beobachtete Häufigkeit). Schließlich werden die Zählungen normalisiert.
Diese Diagramme werden in der Prognoseliteratur üblicherweise als „Zuverlässigkeitsdiagramme“ bezeichnet, obwohl sie auch als „Kalibrierungsdiagramme“ oder -kurven bezeichnet werden können, da sie zusammenfassen, wie gut die Prognosewahrscheinlichkeiten kalibriert sind.
Je besser kalibriert oder zuverlässiger eine Vorhersage ist, desto näher erscheinen die Punkte entlang der Hauptdiagonale von links unten nach rechts oben im Diagramm.
Die Position der Punkte oder der Kurve relativ zur Diagonale kann bei der Interpretation der Wahrscheinlichkeiten helfen; zum Beispiel:
- Unterhalb der Diagonale: Das Modell hat überprognostiziert; die Wahrscheinlichkeiten sind zu groß.
- Oberhalb der Diagonale: Das Modell hat unterprognostiziert; die Wahrscheinlichkeiten sind zu klein.
Wahrscheinlichkeiten sind per Definition kontinuierlich, daher erwarten wir eine gewisse Abweichung von der Linie, die oft als S-förmige Kurve dargestellt wird und pessimistische Tendenzen zeigt, die niedrige Wahrscheinlichkeiten überprognostizieren und hohe Wahrscheinlichkeiten unterprognostizieren.
Wahrscheinlichkeitsdiagramme bieten eine Diagnose, um zu prüfen, ob der Prognosewert Xi zuverlässig ist. Grob gesagt, ist eine Wahrscheinlichkeitsprognose zuverlässig, wenn das Ereignis tatsächlich mit einer beobachteten relativen Häufigkeit eintritt, die mit dem Prognosewert übereinstimmt.
– Increasing the Reliability of Reliability Diagrams, 2007.
Das Zuverlässigkeitsdiagramm kann helfen, die relative Kalibrierung der Vorhersagen aus verschiedenen Vorhersagemodellen zu verstehen.
Willst du Wahrscheinlichkeit für maschinelles Lernen lernen
Nimm jetzt meinen kostenlosen 7-Tage-E-Mail-Crashkurs (mit Beispielcode).
Klicken Sie, um sich anzumelden und auch eine kostenlose PDF-Ebook-Version des Kurses zu erhalten.
Laden Sie sich Ihren KOSTENLOSEN Mini-Kurs herunter
Wahrscheinlichkeitskalibrierung
Die Vorhersagen eines Vorhersagemodells können kalibriert werden.
Kalibrierte Vorhersagen können (oder auch nicht) zu einer verbesserten Kalibrierung in einem Zuverlässigkeitsdiagramm führen.
Einige Algorithmen sind so angepasst, dass ihre vorhergesagten Wahrscheinlichkeiten bereits kalibriert sind. Ohne ins Detail zu gehen, warum, ist die logistische Regression ein solches Beispiel.
Andere Algorithmen erzeugen keine direkten Vorhersagen von Wahrscheinlichkeiten, und stattdessen muss eine Vorhersage von Wahrscheinlichkeiten angenähert werden. Einige Beispiele sind neuronale Netze, Support-Vektor-Maschinen und Entscheidungsbäume.
Die von diesen Methoden vorhergesagten Wahrscheinlichkeiten sind wahrscheinlich unkalibriert und können von einer Modifizierung durch Kalibrierung profitieren.
Die Kalibrierung von Vorhersagewahrscheinlichkeiten ist ein Skalierungsvorgang, der angewendet wird, nachdem die Vorhersagen von einem Vorhersagemodell gemacht wurden.
Es gibt zwei beliebte Ansätze zur Kalibrierung von Wahrscheinlichkeiten; sie sind die Platt-Skalierung und die Isotonische Regression.
Die Platt-Skalierung ist einfacher und eignet sich für Zuverlässigkeitsdiagramme mit der S-Form. Isotonische Regression ist komplexer, erfordert viel mehr Daten (sonst kann es zu einer Überanpassung kommen), kann aber Zuverlässigkeitsdiagramme mit verschiedenen Formen unterstützen (ist nichtparametrisch).
Platt Scaling ist am effektivsten, wenn die Verzerrung in den vorhergesagten Wahrscheinlichkeiten sigmoidförmig ist. Die isotonische Regression ist eine leistungsfähigere Kalibrierungsmethode, die jede monotone Verzerrung korrigieren kann. Leider hat diese zusätzliche Leistung ihren Preis. Eine Lernkurvenanalyse zeigt, dass die Isotonische Regression anfälliger für Überanpassung ist und daher bei knappen Daten schlechter abschneidet als die Platt-Skalierung.
– Predicting Good Probabilities With Supervised Learning, 2005.
Hinweis, und das ist wirklich wichtig: Besser kalibrierte Wahrscheinlichkeiten können zu besseren klassenbasierten oder wahrscheinlichkeitsbasierten Vorhersagen führen oder auch nicht. Es hängt wirklich von der spezifischen Metrik ab, die zur Bewertung der Vorhersagen verwendet wird.
In der Tat deuten einige empirische Ergebnisse darauf hin, dass die Algorithmen, die am meisten von der Kalibrierung der Vorhersagewahrscheinlichkeiten profitieren können, SVMs, Bagged Decision Trees und Random Forests sind.
Nach der Kalibrierung sind die besten Methoden Boosted Trees, Random Forests und SVMs.
– Predicting Good Probabilities With Supervised Learning, 2005.
Wie man Wahrscheinlichkeiten in Python kalibriert
Mit der scikit-learn-Bibliothek für maschinelles Lernen können Sie sowohl die Wahrscheinlichkeitskalibrierung eines Klassifikators diagnostizieren als auch einen Klassifikator kalibrieren, der Wahrscheinlichkeiten vorhersagen kann.
Diagnose der Kalibrierung
Sie können die Kalibrierung eines Klassifikators diagnostizieren, indem Sie ein Zuverlässigkeitsdiagramm der tatsächlichen Wahrscheinlichkeiten gegenüber den vorhergesagten Wahrscheinlichkeiten auf einem Testset erstellen.
In scikit-learn wird dies als Kalibrierungskurve bezeichnet.
Dies kann implementiert werden, indem Sie zunächst die Funktion calibration_curve() berechnen. Diese Funktion nimmt die wahren Klassenwerte für einen Datensatz und die vorhergesagten Wahrscheinlichkeiten für die Hauptklasse (Klasse=1). Die Funktion gibt die wahren Wahrscheinlichkeiten für jedes Bin und die vorhergesagten Wahrscheinlichkeiten für jedes Bin zurück. Die Anzahl der Bins kann über das Argument n_bins angegeben werden und ist standardmäßig auf 5 festgelegt.
Nachfolgend ein Beispiel für einen Codeausschnitt, der die Verwendung der API zeigt:
|
1
2
3
4
5
6
7
8
9
10
|
…
# Wahrscheinlichkeiten vorhersagen
probs = model.predic_proba(testX)
# Zuverlässigkeitsdiagramm
fop, mpv = calibration_curve(testy, probs, n_bins=10)
# plot perfectly calibrated
pyplot.plot(, , linestyle=‘–‚)
# plot model reliability
pyplot.plot(mpv, fop, marker=‘.‘)
pyplot.show()
|
Klassifikator kalibrieren
Ein Klassifikator kann in scikit-learn mithilfe der Klasse CalibratedClassifierCV kalibriert werden.
Es gibt zwei Möglichkeiten, diese Klasse zu verwenden: prefit und cross-validation.
Sie können ein Modell auf einem Trainingsdatensatz anpassen und dieses Prefit-Modell mit einem Hold-Out-Validierungsdatensatz kalibrieren.
Nachfolgend finden Sie beispielsweise einen Codeausschnitt, der die Verwendung der API zeigt:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
…
# Daten vorbereiten
trainX, trainy = …
valX, valy = …
testX, testy = …
# fit base model on training dataset
model = …
model.fit(trainX, trainy)
# Modell auf Validierungsdaten kalibrieren
calibrator = CalibratedClassifierCV(model, cv=’prefit‘)
calibrator.fit(valX, valy)
# das Modell auswerten
yhat = calibrator.predict(testX)
|
Alternativ kann der CalibratedClassifierCV mehrere Kopien des Modells unter Verwendung der k-fachen Kreuzvalidierung anpassen und die von diesen Modellen vorhergesagten Wahrscheinlichkeiten unter Verwendung des Hold-out-Sets kalibrieren. Vorhersagen werden mit jedem der trainierten Modelle gemacht.
Nachfolgend finden Sie einen Codeschnipsel, der die Verwendung der API zeigt:
|
1
2
3
4
5
6
7
8
9
10
11
|
…
# Daten vorbereiten
trainX, trainy = …
testX, testy = …
# Basismodell definieren
model = …
# Modell auf Trainingsdaten anpassen und kalibrieren
calibrator = CalibratedClassifierCV(model, cv=3)
calibrator.fit(trainX, trainy)
# das Modell auswerten
yhat = calibrator.predict(testX)
|
Die Klasse CalibratedClassifierCV unterstützt zwei Arten der Wahrscheinlichkeitskalibrierung, nämlich die parametrische ‚Sigmoid‘-Methode (Platt’sche Methode) und die nichtparametrische ‚isotonische‘ Methode, die über das Argument ‚Methode‘ angegeben werden kann.
Arbeitsbeispiel zur Kalibrierung von SVM-Wahrscheinlichkeiten
Wir können die Diskussion der Kalibrierung mit einigen Arbeitsbeispielen konkretisieren.
In diesen Beispielen werden wir eine Support-Vektor-Maschine (SVM) an ein verrauschtes binäres Klassifikationsproblem anpassen und das Modell zur Vorhersage von Wahrscheinlichkeiten verwenden, dann die Kalibrierung mithilfe eines Zuverlässigkeitsdiagramms überprüfen und den Klassifikator kalibrieren und das Ergebnis überprüfen.
Die SVM ist ein guter Kandidat für die Kalibrierung, da sie nicht von Haus aus Wahrscheinlichkeiten vorhersagt, was bedeutet, dass die Wahrscheinlichkeiten oft unkalibriert sind.
Ein Hinweis zur SVM: Wahrscheinlichkeiten können durch den Aufruf der Funktion decision_function() für das angepasste Modell anstelle der üblichen Funktion predict_proba() vorhergesagt werden. Die Wahrscheinlichkeiten sind nicht normalisiert, können aber beim Aufruf der Funktion calibration_curve() normalisiert werden, indem das Argument ’normalize‘ auf ‚True‘ gesetzt wird.
Das folgende Beispiel passt ein SVM-Modell auf das Testproblem an, sagt Wahrscheinlichkeiten voraus und stellt die Kalibrierung der Wahrscheinlichkeiten als Zuverlässigkeitsdiagramm dar,
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
# SVM Zuverlässigkeitsdiagramm
from sklearn.datasets import make_classification
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.calibration import calibration_curve
from matplotlib import pyplot
# generate 2 class dataset
X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# fit a model
model = SVC()
model.fit(trainX, trainy)
# predict probabilities
probs = model.decision_function(testX)
# Zuverlässigkeitsdiagramm
fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True)
# plot perfekt kalibriert
pyplot.plot(, , linestyle=‘–‚)
# plot model reliability
pyplot.plot(mpv, fop, marker=‘.‘)
pyplot.show()
|
Das Ausführen des Beispiels erzeugt ein Zuverlässigkeitsdiagramm, das die Kalibrierung der von den SVMs vorhergesagten Wahrscheinlichkeiten (durchgezogene Linie) im Vergleich zu einem perfekt kalibrierten Modell entlang der Diagonale des Diagramms (gestrichelte Linie) zeigt.)
Wir können die erwartete S-förmige Kurve einer konservativen Vorhersage sehen.
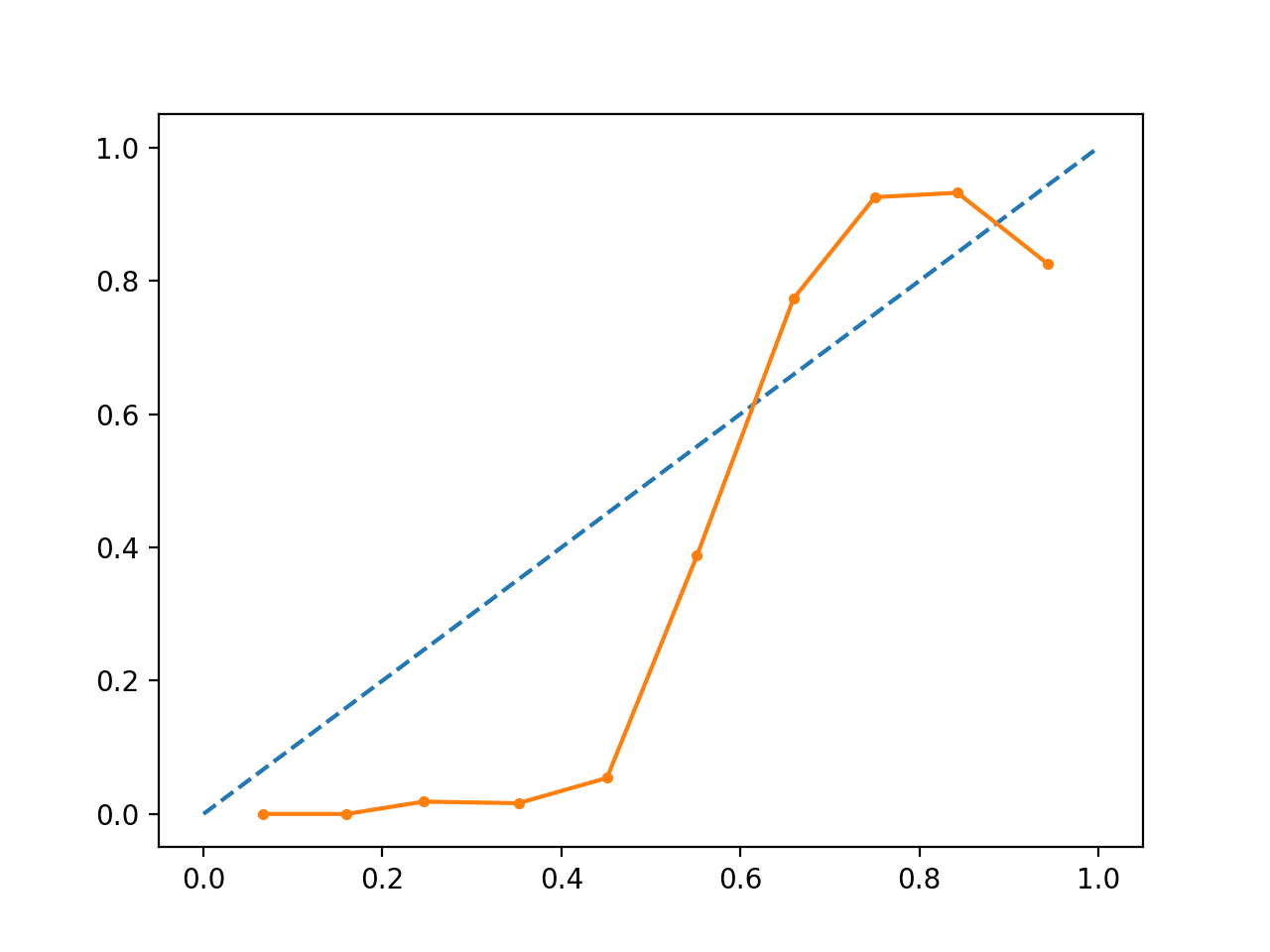
Unkalibriertes SVM-Reliabilitätsdiagramm
Wir können das Beispiel aktualisieren, um das SVM über die Klasse CalibratedClassifierCV mit 5-facher Kreuzvalidierung anzupassen, wobei die Holdout-Sets zur Kalibrierung der vorhergesagten Wahrscheinlichkeiten verwendet werden.
Das vollständige Beispiel ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# SVM Zuverlässigkeitsdiagramm mit Kalibrierung
from sklearn.datasets import make_classification
from sklearn.svm import SVC
from sklearn.calibration import CalibratedClassifierCV
from sklearn.model_selection import train_test_split
from sklearn.calibration import calibration_curve
from matplotlib import pyplot
# generate 2 class dataset
X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1)
# split into train/test sets
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# fit a model
model = SVC()
calibrated = CalibratedClassifierCV(model, method=’sigmoid‘, cv=5)
calibrated.fit(trainX, trainy)
# Vorhersagewahrscheinlichkeiten
probs = calibrated.predict_proba(testX)
# Zuverlässigkeitsdiagramm
fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True)
# plot perfectly calibrated
pyplot.plot(, , linestyle=‘–‚)
# Plot kalibrierte Zuverlässigkeit
pyplot.plot(mpv, fop, marker=‘.‘)
pyplot.show()
|
Die Ausführung des Beispiels erzeugt ein Zuverlässigkeitsdiagramm für die kalibrierten Wahrscheinlichkeiten.
Die Form der kalibrierten Wahrscheinlichkeiten ist anders, sie passen sich viel besser an die diagonale Linie an, obwohl sie im oberen Quadranten immer noch zu niedrig prognostiziert werden.
Aus dem Diagramm geht hervor, dass das kalibrierte Modell besser ist.
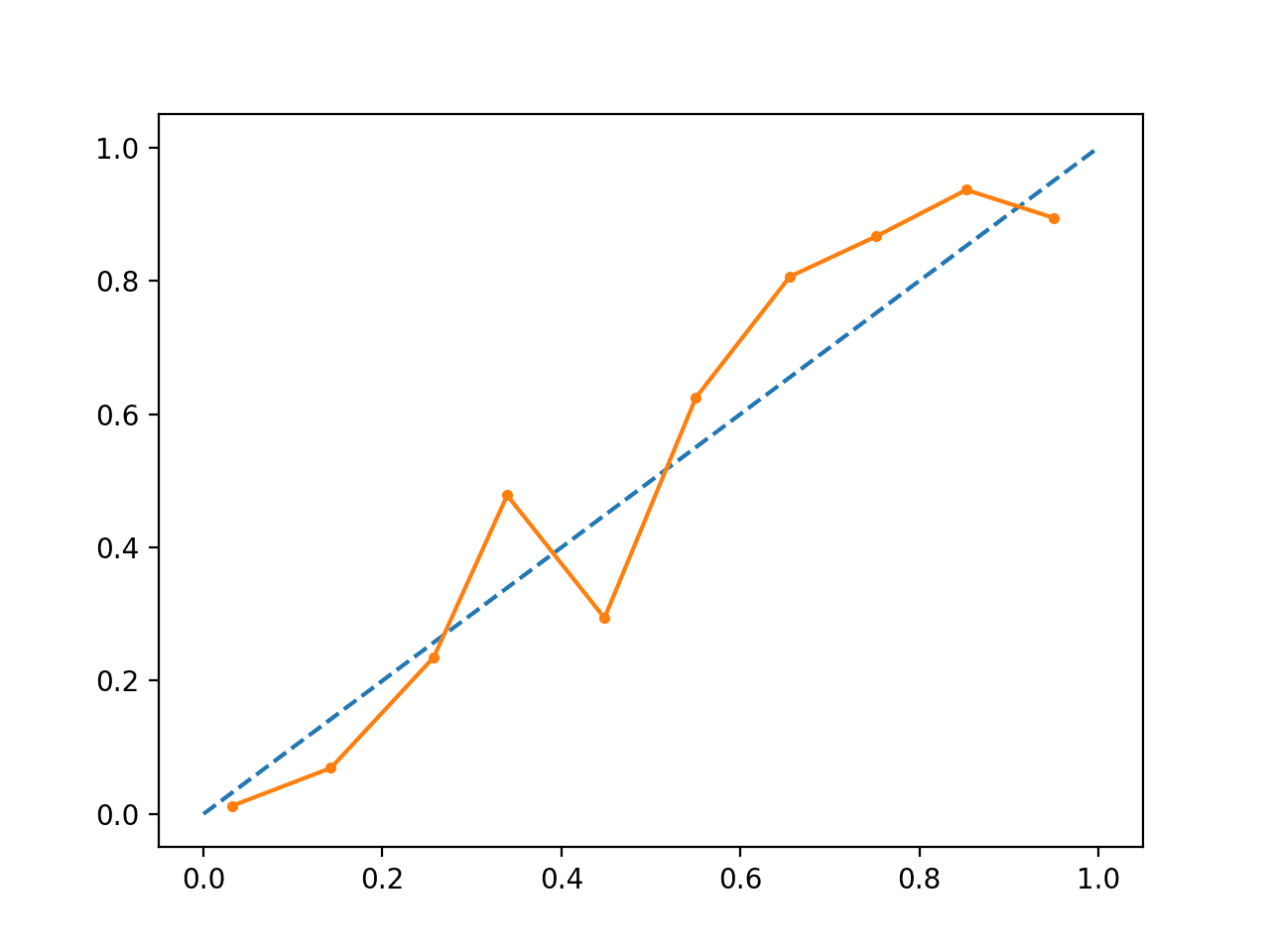
Kalibriertes SVM-Zuverlässigkeitsdiagramm
Wir können den Kontrast zwischen den beiden Modellen noch deutlicher machen, indem wir beide Zuverlässigkeitsdiagramme in denselben Plot einfügen.
Das vollständige Beispiel ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
# SVM-Zuverlässigkeitsdiagramme mit unkalibrierten und kalibrierten Wahrscheinlichkeiten
from sklearn.datasets import make_classification
from sklearn.svm import SVC
from sklearn.calibration import CalibratedClassifierCV
from sklearn.model_selection import train_test_split
from sklearn.calibration import calibration_curve
from matplotlib import pyplot
# unkalibrierte Wahrscheinlichkeiten vorhersagen
def uncalibrated(trainX, testX, trainy):
# fit a model
model = SVC()
model.fit(trainX, trainy)
# predict probabilities
return model.decision_function(testX)
# predict calibrated probabilities
def calibrated(trainX, testX, trainy):
# Modell definieren
model = SVC()
# Kalibrierungsmodell definieren und anpassen
calibrated = CalibratedClassifierCV(model, method=’sigmoid‘, cv=5)
calibrated.fit(trainX, trainy)
# Wahrscheinlichkeiten vorhersagen
return calibrated.predict_proba(testX)
# 2-Klassen-Datensatz erzeugen
X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1)
# in train/test-Sätze aufteilen
trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2)
# unkalibrierte Vorhersagen
yhat_unkalibriert = unkalibriert(trainX, testX, trainy)
# kalibrierte Vorhersagen
yhat_calibrated = calibrated(trainX, testX, trainy)
# Zuverlässigkeitsdiagramme
fop_uncalibrated, mpv_unkalibriert = calibration_curve(testy, yhat_unkalibriert, n_bins=10, normalize=True)
fop_kalibriert, mpv_kalibriert = calibration_curve(testy, yhat_kalibriert, n_bins=10)
# plot perfekt kalibriert
pyplot.plot(, , linestyle=‘–‚, color=’black‘)
# plot model reliabilities
pyplot.plot(mpv_uncalibrated, fop_uncalibrated, marker=‘.‘)
pyplot.plot(mpv_calibrated, fop_calibrated, marker=‘.‘)
pyplot.show()
|
Das Ausführen des Beispiels erzeugt ein einzelnes Zuverlässigkeitsdiagramm, das sowohl die kalibrierten (orange) als auch die unkalibrierten (blau) Wahrscheinlichkeiten anzeigt.
Es ist nicht wirklich ein Vergleich von Äpfeln zu Äpfeln, da die Vorhersagen des kalibrierten Modells in Wirklichkeit eine Kombination aus fünf Teilmodellen sind.
Nichtsdestotrotz sehen wir einen deutlichen Unterschied in der Zuverlässigkeit der kalibrierten Wahrscheinlichkeiten (sehr wahrscheinlich durch den Kalibrierungsprozess verursacht).
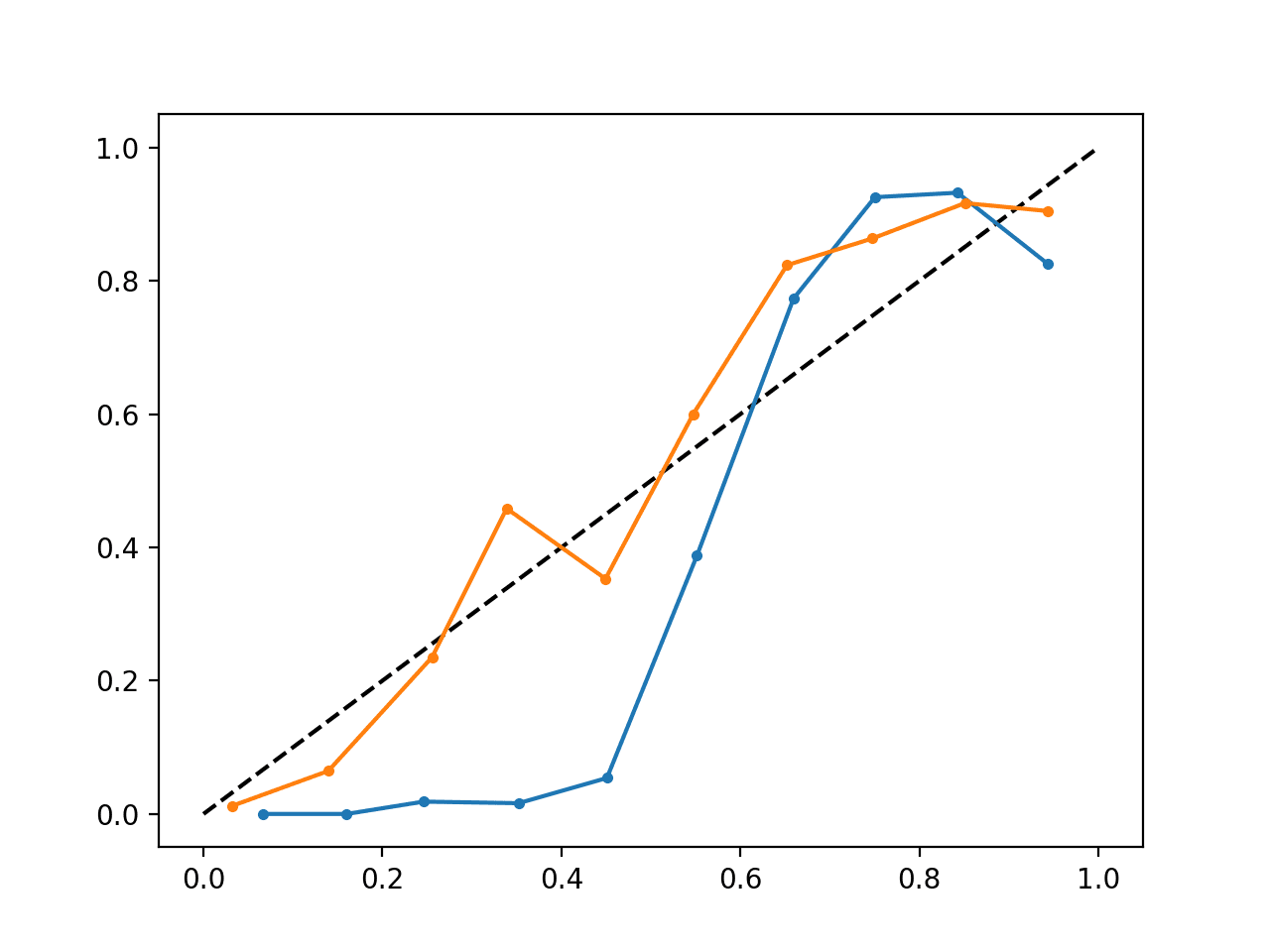
Kalibriertes und unkalibriertes SVM-Reliabilitätsdiagramm
Weitere Lektüre
In diesem Abschnitt finden Sie weitere Ressourcen zu diesem Thema, wenn Sie tiefer einsteigen möchten.
Bücher und Aufsätze
- Applied Predictive Modeling, 2013.
- Predicting Good Probabilities With Supervised Learning, 2005.
- Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers, 2001.
- Erhöhen der Zuverlässigkeit von Zuverlässigkeitsdiagrammen, 2007.
API
- sklearn.calibration.CalibratedClassifierCV API
- sklearn.calibration.calibration_curve API
- Wahrscheinlichkeitskalibrierung, scikit-learn User Guide
- Wahrscheinlichkeitskalibrierungskurven, scikit-learn
- Vergleich der Kalibrierung von Klassifikatoren, scikit-learn
Artikel
- CAWCAR Verification Website
- Kalibrierung (Statistik) auf Wikipedia
- Probabilistische Klassifikation auf Wikipedia
- Scikit korrekter Weg zur Kalibrierung von Klassifikatoren mit CalibratedClassifierCV auf CrossValidated
Zusammenfassung
In diesem Lernprogramm, haben Sie die Bedeutung der Kalibrierung von Vorhersagewahrscheinlichkeiten kennengelernt und erfahren, wie Sie die Kalibrierung von Modellen, die für probabilistische Klassifikation verwendet werden, diagnostizieren und verbessern können.
Speziell haben Sie gelernt:
- Nichtlineare Algorithmen für maschinelles Lernen sagen oft unkalibrierte Klassenwahrscheinlichkeiten voraus.
- Zuverlässigkeitsdiagramme können verwendet werden, um die Kalibrierung eines Modells zu diagnostizieren, und Methoden können verwendet werden, um die Vorhersagen für ein Problem besser zu kalibrieren.
- Wie man Zuverlässigkeitsdiagramme entwickelt und Klassifikationsmodelle in Python mit scikit-learn kalibriert.
Haben Sie Fragen?
Setzen Sie sich mit Ihren Fragen in den Kommentaren unten auseinander und ich werde mein Bestes tun, um zu antworten.
Get a Handle on Probability for Machine Learning!

Develop your Understanding of Probability
…mit nur ein paar Zeilen Python-Code
Entdecken Sie in meinem neuen Ebook:
Probability for Machine Learning
Es bietet Selbstlern-Tutorials und durchgängige Projekte zu:
Bayes-Theorem, Bayes’sche Optimierung, Verteilungen, Maximum Likelihood, Cross-Entropie, Kalibrierung von Modellen
und vielem mehr….
Nutzen Sie endlich die Unsicherheit in Ihren Projekten
Überspringen Sie die akademische Seite. Just Results.See What’s Inside