Hi Glenn,

p> Vou assumir que se está a lidar com um octógono regular.

P>Primeiro precisa de saber quantas diagonais tem um octógono regular e depois quantas têm o comprimento mais longo. Desenhe um octógono, seleccione um vértice e construa cada diagonal a partir desse vértice. Verá que existem 5 diagonais.

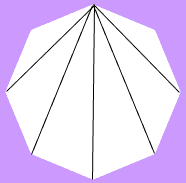
Assim, para cada um dos 8 vértices, pode desenhar 5 diagonais e, portanto, construiu 5 8 = 40 diagonais. Mas construiu cada diagonal duas vezes, uma vez a partir de cada uma das suas extremidades. Assim, existem 20 diagonais num octógono regular.

Um olhar para o diagrama acima mostra que uma das diagonais construídas é mais longa do que as outras. Assim, constrói-se uma diagonal longa a partir de cada vértice, e portanto 8 diagonais longas. Mais uma vez, construímos cada uma duas vezes, pelo que existem 4 diagonais compridas. Assim, se seleccionar uma diagonal de todas as diagonais num octógono regular, há 4 probabilidades em 20 de seleccionar uma das mais longas, e portanto uma probabilidade de 4/20 = 1/5.

E a mais curta?

Andrei e Penny