Dernière mise à jour le 25 septembre 2019

Au lieu de prédire directement les valeurs des classes pour un problème de classification, il peut être pratique de prédire la probabilité qu’une observation appartienne à chaque classe possible.

Prédire les probabilités permet une certaine flexibilité, notamment de décider comment interpréter les probabilités, de présenter les prédictions avec incertitude et de fournir des moyens plus nuancés d’évaluer la compétence du modèle.

Les probabilités prédites qui correspondent à la distribution attendue des probabilités pour chaque classe sont dites calibrées. Le problème est que tous les modèles d’apprentissage automatique ne sont pas capables de prédire des probabilités calibrées.

Il existe des méthodes permettant à la fois de diagnostiquer le degré de calibrage des probabilités prédites et de mieux calibrer les probabilités prédites avec la distribution observée de chaque classe. Souvent, cela peut conduire à des prédictions de meilleure qualité, selon la façon dont la compétence du modèle est évaluée.

Dans ce tutoriel, vous découvrirez l’importance de la calibration des probabilités prédites et comment diagnostiquer et améliorer la calibration des modèles utilisés pour la classification probabiliste.

Après avoir terminé ce tutoriel, vous saurez :

• Les algorithmes d’apprentissage automatique non linéaires prédisent souvent des probabilités de classe non calibrées.
• Les diagrammes de fiabilité peuvent être utilisés pour diagnostiquer la calibration d’un modèle, et des méthodes peuvent être utilisées pour mieux calibrer les prédictions pour un problème.
• Comment développer des diagrammes de fiabilité et calibrer des modèles de classification en Python avec scikit-learn.

Démarrez votre projet avec mon nouveau livre Probability for Machine Learning, comprenant des tutoriels étape par étape et les fichiers de code source Python pour tous les exemples.

Démarrons.

Comment et quand utiliser un modèle de classification calibré avec scikit-learn
Photo de Nigel Howe, certains droits réservés.

Vue d’ensemble du tutoriel

Ce tutoriel est divisé en quatre parties ; ce sont :

1. Prédire les probabilités
2. Calibration des prédictions
3. Comment calibrer les probabilités en Python
4. Exemple fonctionnel de calibration des probabilités SVM

Prédire les probabilités

Un problème de modélisation prédictive de classification nécessite de prédire ou de prévoir une étiquette pour une observation donnée.

Au lieu de prédire directement l’étiquette, un modèle peut prédire la probabilité qu’une observation appartienne à chaque étiquette de classe possible.

Cela offre une certaine flexibilité à la fois dans la façon dont les prédictions sont interprétées et présentées (choix du seuil et de l’incertitude de prédiction) et dans la façon dont le modèle est évalué.

Bien qu’un modèle puisse être capable de prédire des probabilités, la distribution et le comportement des probabilités peuvent ne pas correspondre à la distribution attendue des probabilités observées dans les données d’apprentissage.

Ceci est particulièrement fréquent avec les algorithmes d’apprentissage automatique non linéaires complexes qui ne font pas directement de prédictions probabilistes et utilisent plutôt des approximations.

La distribution des probabilités peut être ajustée pour mieux correspondre à la distribution attendue observée dans les données. Cet ajustement est appelé calibration, comme dans la calibration du modèle ou la calibration de la distribution des probabilités de classe.

nous souhaitons que les probabilités de classe estimées reflètent la véritable probabilité sous-jacente de l’échantillon. Autrement dit, la probabilité de classe prédite (ou valeur semblable à une probabilité) doit être bien calibrée. Pour être bien calibrées, les probabilités doivent effectivement refléter la vraie probabilité de l’événement d’intérêt.

– Page 249, Applied Predictive Modeling, 2013.

Calibration des prédictions

Il y a deux préoccupations dans la calibration des probabilités ; ce sont le diagnostic de la calibration des probabilités prédites et le processus de calibration lui-même.

Diagrammes de fiabilité (courbes de calibrage)

Un diagramme de fiabilité est un tracé linéaire de la fréquence relative de ce qui a été observé (axe des ordonnées) par rapport à la fréquence de probabilité prédite (axe des abscisses).

Les diagrammes de fiabilité sont des aides courantes pour illustrer les propriétés des systèmes de prévision probabiliste. Ils consistent en un tracé de la fréquence relative observée par rapport à la probabilité prédite, fournissant une intercomparaison visuelle rapide lors du réglage des systèmes de prévision probabiliste, ainsi que la documentation de la performance du produit final

– Increasing the Reliability of Reliability Diagrams, 2007.

Spécifiquement, les probabilités prédites sont divisées en un nombre fixe de godets le long de l’axe des x. Le nombre d’événements (class=1) est ensuite compté pour chaque bac (par exemple, la fréquence relative observée). Enfin, les comptes sont normalisés. Les résultats sont ensuite représentés sous forme de tracé linéaire.

Ces tracés sont communément appelés diagrammes de  » fiabilité  » dans la littérature sur les prévisions, bien qu’ils puissent également être appelés tracés ou courbes de  » calibration « , car ils résument la façon dont les probabilités de prévision sont calibrées.

Plus une prévision est calibrée ou fiable, plus les points apparaîtront proches le long de la diagonale principale, du bas à gauche au haut à droite du tracé.

La position des points ou de la courbe par rapport à la diagonale peut aider à interpréter les probabilités ; par exemple :

• En dessous de la diagonale : Le modèle a sur-prévu ; les probabilités sont trop importantes.
• Au-dessus de la diagonale : Le modèle a sous-estimé ; les probabilités sont trop faibles.

Les probabilités, par définition, sont continues, nous nous attendons donc à une certaine séparation de la ligne, souvent représentée par une courbe en forme de S montrant des tendances pessimistes surestimant les faibles probabilités et sous-estimant les fortes probabilités.

Les diagrammes de fiabilité fournissent un diagnostic permettant de vérifier si la valeur prévue Xi est fiable. Grosso modo, une prévision de probabilité est fiable si l’événement se produit effectivement avec une fréquence relative observée cohérente avec la valeur prévue.

– Augmenter la fiabilité des diagrammes de fiabilité, 2007.

Le diagramme de fiabilité peut aider à comprendre la calibration relative des prévisions de différents modèles prédictifs.

Calibrage des probabilités

Les prédictions faites par un modèle prédictif peuvent être calibrées.

Les prédictions calibrées peuvent (ou non) entraîner une amélioration de la calibration sur un diagramme de fiabilité.

Certains algorithmes sont ajustés de telle sorte que leurs probabilités prédites sont déjà calibrées. Sans entrer dans les détails pourquoi, la régression logistique est un tel exemple.

D’autres algorithmes ne produisent pas directement des prédictions de probabilités, et au lieu de cela une prédiction de probabilités doit être approximée. Quelques exemples incluent les réseaux neuronaux, les machines à vecteurs de support et les arbres de décision.

Les probabilités prédites par ces méthodes seront probablement non calibrées et peuvent bénéficier d’être modifiées via la calibration.

La calibration des probabilités de prédiction est une opération de remise à l’échelle qui est appliquée après que les prédictions ont été faites par un modèle prédictif.

Il existe deux approches populaires pour calibrer les probabilités ; ce sont la mise à l’échelle de Platt et la régression isotonique.

La mise à l’échelle de Platt est plus simple et convient aux diagrammes de fiabilité en forme de S. La Régression isotonique est plus complexe, nécessite beaucoup plus de données (sinon, elle risque de se surajuster), mais peut prendre en charge des diagrammes de fiabilité de différentes formes (elle est non paramétrique).

L’échelonnement de Platt est plus efficace lorsque la distorsion des probabilités prédites est de forme sigmoïde. La régression isotonique est une méthode de calibrage plus puissante qui peut corriger toute distorsion monotone. Malheureusement, cette puissance supplémentaire a un prix. Une analyse de la courbe d’apprentissage montre que la régression isotonique est plus encline au surajustement, et qu’elle est donc moins performante que l’échelle de Platt, lorsque les données sont rares.

– Predicting Good Probabilities With Supervised Learning, 2005.

Note, et c’est vraiment important : des probabilités mieux calibrées peuvent ou non conduire à de meilleures prédictions basées sur la classe ou sur les probabilités. Cela dépend vraiment de la métrique spécifique utilisée pour évaluer les prédictions.

En fait, certains résultats empiriques suggèrent que les algorithmes qui peuvent bénéficier le plus de la calibration des probabilités prédites incluent les SVM, les arbres de décision en sac et les forêts aléatoires.

après calibration, les meilleures méthodes sont les arbres boostés, les forêts aléatoires et les SVM.

– Prédire de bonnes probabilités avec l’apprentissage supervisé, 2005.

Comment calibrer les probabilités en Python

La bibliothèque d’apprentissage automatique scikit-learn vous permet à la fois de diagnostiquer le calibrage des probabilités d’un classificateur et de calibrer un classificateur capable de prédire les probabilités.

Diagnostiquer le calibrage

Vous pouvez diagnostiquer le calibrage d’un classificateur en créant un diagramme de fiabilité des probabilités réelles par rapport aux probabilités prédites sur un ensemble de test.

En scikit-learn, cela s’appelle une courbe de calibrage.

Cela peut être mis en œuvre en calculant d’abord la fonction calibration_curve(). Cette fonction prend les vraies valeurs de classe pour un ensemble de données et les probabilités prédites pour la classe principale (class=1). La fonction renvoie les probabilités réelles pour chaque bin et les probabilités prédites pour chaque bin. Le nombre de bacs peut être spécifié via l’argument n_bins et la valeur par défaut est de 5.

Par exemple, voici un extrait de code montrant l’utilisation de l’API :

. .

Calibrer un classificateur

Un classificateur peut être calibré dans scikit-learn à l’aide de la classe CalibratedClassifierCV.

Il existe deux façons d’utiliser cette classe : le prefit et la validation croisée.

Vous pouvez ajuster un modèle sur un ensemble de données d’entraînement et calibrer ce modèle de pré-affectation en utilisant un ensemble de données de validation de retenue.

Par exemple, voici un extrait de code montrant l’utilisation de l’API :

Alternativement, le CalibratedClassifierCV peut ajuster plusieurs copies du modèle en utilisant la validation croisée k-fold et calibrer les probabilités prédites par ces modèles en utilisant l’ensemble hold out. Les prédictions sont faites en utilisant chacun des modèles entraînés.

Par exemple, voici un extrait de code montrant l’utilisation de l’API :

.>.

1 2 3 4 5 6 7 8 . 9 10 11

… # préparer les données trainX, trainy = … testX, testy = … # définir le modèle de base modèle = … # ajuster et calibrer le modèle sur les données d’entraînement calibrateur = CalibratedClassifierCV(modèle, cv=3) calibrateur.fit(trainX, trainy) # évaluer le modèle yhat = calibrateur.predict(testX)

La classe CalibratedClassifierCV prend en charge deux types de calibration de probabilité ; plus précisément, la méthode paramétrique ‘sigmoïde’ (méthode de Platt) et la méthode non paramétrique ‘isotonique’ qui peut être spécifiée via l’argument ‘method’.

Exemple travaillé de calibration des probabilités SVM

Nous pouvons rendre la discussion sur la calibration concrète avec quelques exemples travaillés.

Dans ces exemples, nous allons adapter une machine à vecteurs de support (SVM) à un problème de classification binaire bruyant et utiliser le modèle pour prédire les probabilités, puis revoir la calibration à l’aide d’un diagramme de fiabilité et calibrer le classificateur et revoir le résultat.

Le SVM est un bon modèle candidat à calibrer car il ne prédit pas nativement les probabilités, ce qui signifie que les probabilités sont souvent non calibrées.

Une note sur le SVM : les probabilités peuvent être prédites en appelant la fonction decision_function() sur le modèle ajusté au lieu de la fonction habituelle predict_proba(). Les probabilités ne sont pas normalisées, mais peuvent l’être lors de l’appel de la fonction calibration_curve() en fixant l’argument ‘normalize’ à ‘True’.

L’exemple ci-dessous ajuste un modèle SVM sur le problème de test, prédit les probabilités, et trace la calibration des probabilités sous forme de diagramme de fiabilité,

1 2 3 4 5 6 7 8 9 10 . 11 12 13 14 15 16 17 18 19 20 21 22

# Diagramme de fiabilité SVM from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # split into train/test sets trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # ajuster un modèle modèle = SVC() modèle.fit(trainX, trainy) # prédire les probabilités probs = modèle.decision_function(testX) # diagramme de fiabilité fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot parfaitement calibré pyplot.plot(, , linestyle=’–‘) # plot fiabilité du modèle pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

L’exécution de l’exemple crée un diagramme de fiabilité montrant le calibrage des probabilités prédites par les SVM (ligne pleine) par rapport à un modèle parfaitement calibré le long de la diagonale du tracé (ligne pointillée.)

On peut voir la courbe en forme de S attendue d’une prévision conservatrice.

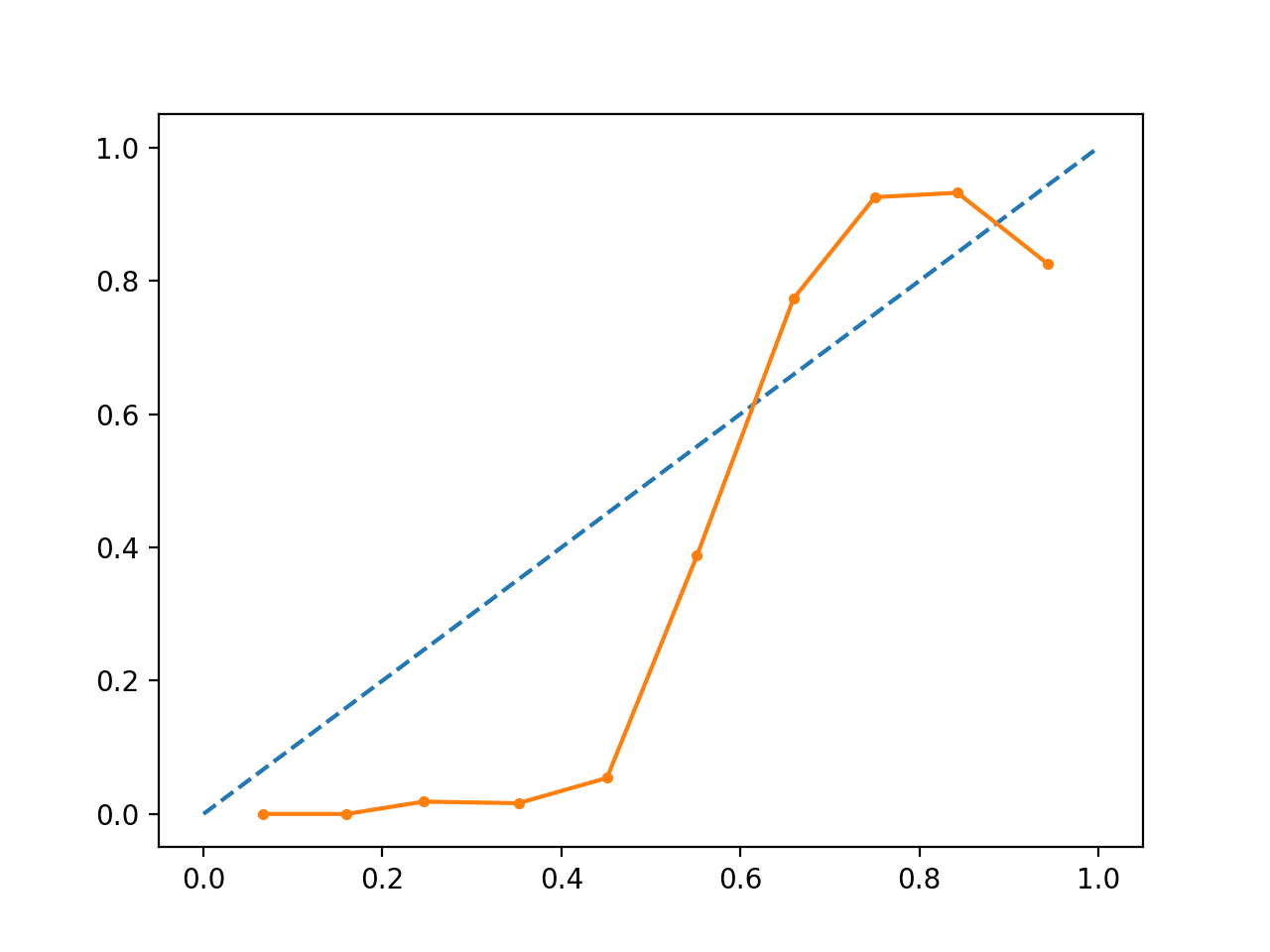
Diagramme de fiabilité du SVM non calibré

Nous pouvons mettre à jour l’exemple pour ajuster le SVM via la classe CalibratedClassifierCV en utilisant la validation croisée 5 fois, en utilisant les ensembles de maintien pour calibrer les probabilités prédites.

L’exemple complet est répertorié ci-dessous.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

# Diagramme de fiabilité SVM avec calibration from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # split into train/test sets trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # ajuster un modèle modèle = SVC() calibré = CalibratedClassifierCV(modèle, method=’sigmoïde’, cv=5) calibré.fit(trainX, trainy) # prédire les probabilités probs = calibré.predict_proba(testX) # diagramme de fiabilité fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # tracer parfaitement calibré pyplot.plot(, , linestyle=’–‘) # tracer la fiabilité calibrée pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

L’exécution de l’exemple crée un diagramme de fiabilité pour les probabilités calibrées.

La forme des probabilités calibrées est différente, épousant beaucoup mieux la diagonale, bien qu’il y ait toujours une sous-prévision dans le quadrant supérieur.

Visuellement, le tracé suggère un meilleur modèle calibré.

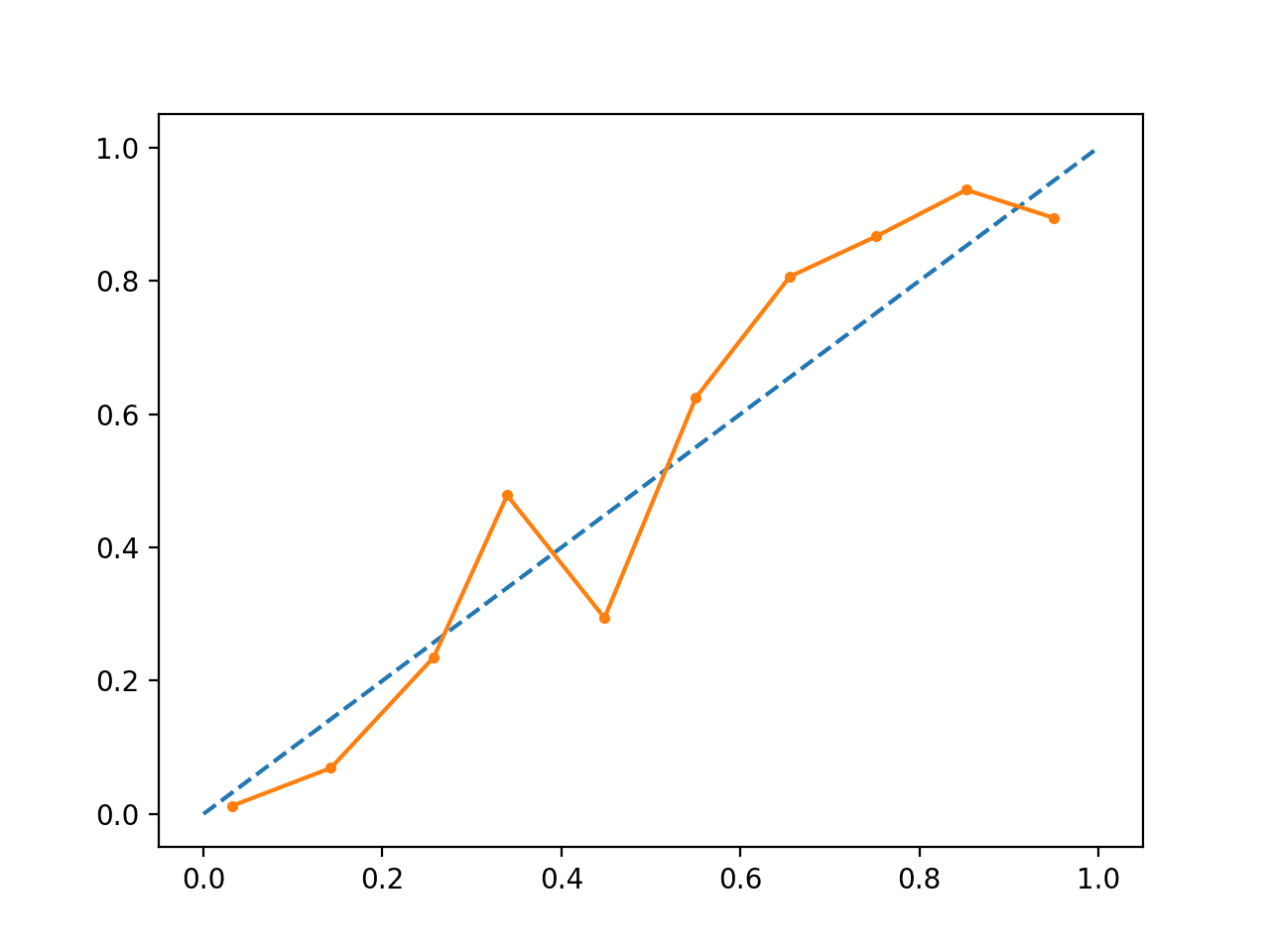
Diagramme de fiabilité du SVM calibré

Nous pouvons rendre le contraste entre les deux modèles plus évident en incluant les deux diagrammes de fiabilité sur le même graphe.

L’exemple complet est repris ci-dessous.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 36 37 38 39 40 41 42 43

# Diagrammes de fiabilité SVM avec probabilités non calibrées et calibrées from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # predict uncalibrated probabilities def uncalibrated(trainX, testX, trainy) : # ajuster un modèle modèle = SVC() modèle.fit(trainX, trainy) # prédire les probabilités return modèle.decision_function(testX) # prédire les probabilités calibrées def calibrated(trainX, testX, trainy) : # définir le modèle modèle = SVC() Définir et ajuster le modèle de calibration calibré = CalibratedClassifierCV(modèle, method=’sigmoïde’, cv=5) calibré.fit(trainX, trainy) # predict probabilities return calibrated.predict_proba(testX) # générer un ensemble de données à 2 classes X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # diviser en ensembles train/test trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # prédictions non calibrées yhat_uncalibrated = uncalibrated(trainX, testX, trainy) # prédictions calibrées yhat_calibrated = calibré(trainX, testX, trainy) # diagrammes de fiabilité fop_uncalibrated, mpv_uncalibrated = calibration_curve(testy, yhat_uncalibrated, n_bins=10, normalize=True) fop_calibrated, mpv_calibrated = calibration_curve(testy, yhat_calibrated, n_bins=10) # plot parfaitement calibré pyplot.plot(, , linestyle=’–‘, color=’black’) # plot model reliabilities pyplot.plot(mpv_uncalibrated, fop_uncalibrated, marker=’.’) pyplot.plot(mpv_calibrated, fop_calibrated, marker=’.’) pyplot.show()

L’exécution de l’exemple crée un seul diagramme de fiabilité montrant à la fois les probabilités calibrées (orange) et non calibrées (bleu).

Il ne s’agit pas vraiment d’une comparaison de pommes à pommes car les prédictions faites par le modèle calibré sont en fait une combinaison de cinq sous-modèles.

Néanmoins, nous constatons une différence marquée dans la fiabilité des probabilités calibrées (très probablement causée par le processus de calibration).

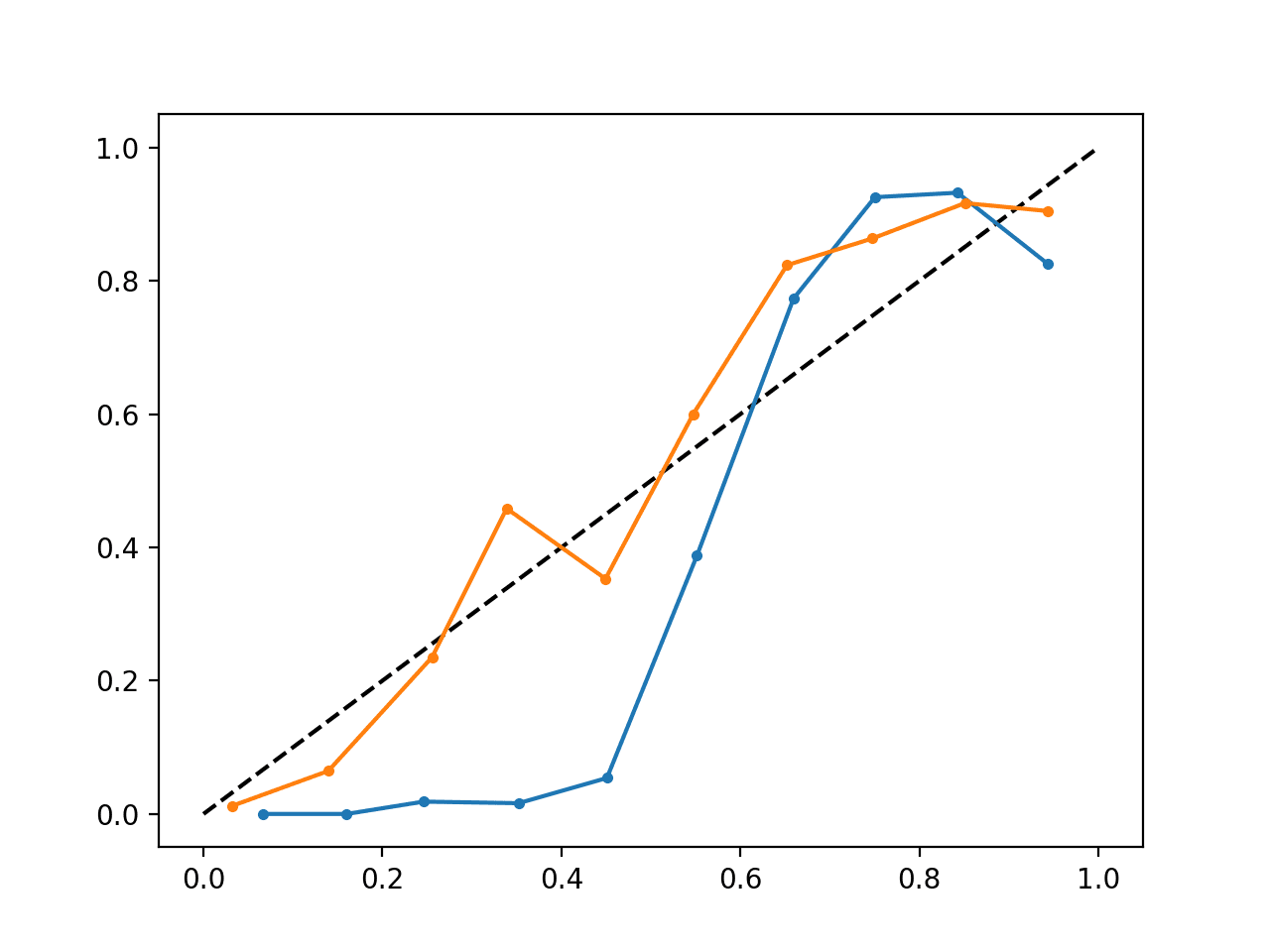
Diagramme de fiabilité du SVM calibré et non calibré

Lectures complémentaires

Cette section fournit d’autres ressources sur le sujet si vous cherchez à approfondir.

Livres et articles

• Modélisation prédictive appliquée, 2013.
• Prédire de bonnes probabilités avec l’apprentissage supervisé, 2005.
• Obtenir des estimations de probabilité calibrées à partir d’arbres de décision et de classificateurs bayésiens naïfs, 2001.
• Augmenter la fiabilité des diagrammes de fiabilité, 2007.

API

• sklearn.calibration.CalibratedClassifierCV API
• sklearn.calibration.calibration_curve API
• Calibration de probabilités, guide utilisateur scikit-learn
• Courbes de calibration de probabilités, scikit-learn
• Comparaison de la calibration de classificateurs, scikit-learn

Articles

• Site de vérification deCAWCAR
• Calibration (statistiques) sur Wikipédia
• Classification probabiliste. sur Wikipedia
• Scikit correct way to calibrate classifiers with CalibratedClassifierCV on CrossValidated

Summary

Dans ce tutoriel, vous avez découvert l’importance de la calibration des probabilités prédites et comment diagnostiquer et améliorer la calibration des modèles utilisés pour la classification probabiliste.

Spécifiquement, vous avez appris :

• Les algorithmes d’apprentissage automatique non linéaires prédisent souvent des probabilités de classe non calibrées.
• Les diagrammes de fiabilité peuvent être utilisés pour diagnostiquer la calibration d’un modèle, et des méthodes peuvent être utilisées pour mieux calibrer les prédictions pour un problème.
• Comment développer des diagrammes de fiabilité et calibrer des modèles de classification en Python avec scikit-learn.

Avez-vous des questions ?
Posez vos questions dans les commentaires ci-dessous et je ferai de mon mieux pour y répondre.

Maîtrisez les probabilités pour l’apprentissage automatique !

Développez votre compréhension des probabilités

….avec seulement quelques lignes de code python

Découvrez comment dans mon nouvel Ebook :
Probabilité pour l’apprentissage automatique

Il fournit des tutoriels d’auto-apprentissage et des projets de bout en bout sur :
le théorème de Bayes, l’optimisation bayésienne, les distributions, la vraisemblance maximale, l’entropie croisée, le calibrage des modèles
et bien plus encore.

Enfin, maîtrisez l’incertitude dans vos projets

Skip the Academics. Voyez ce qu’il y a dedans

Tweet Share Share