Hi Glenn,

Je vais supposer que vous avez affaire à un octogone régulier.

D’abord, vous devez savoir combien de diagonales possède un octogone régulier, puis combien ont la plus grande longueur. Dessinez un octogone, sélectionnez un sommet et construisez chaque diagonale à partir de ce sommet.Vous verrez qu’il y a 5 de ces diagonales.

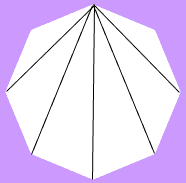
Donc pour chacun des 8 sommets vous pouvez dessiner 5 diagonales et donc vous avez construit 5 8 = 40 diagonales. Mais vous avez construit chaque diagonale deux fois, une fois à partir de chacune de ses extrémités. Il y a donc 20 diagonales dans un octogone régulier.

Un regard sur le schéma ci-dessus montre qu’une des diagonales construites est plus longue que les autres. Ainsi, vous construisez une longue diagonale à partir de chaque sommet, et donc 8 longues diagonales. De nouveau, vous avez construit chacune d’elles deux fois, ce qui donne 4 longues diagonales. Ainsi, si vous choisissez une diagonale parmi toutes les diagonales d’un octogone régulier, il y a 4 chances sur 20 que vous choisissiez l’une des plus longues, et donc une probabilité de 4/20 = 1/5.

Qu’en est-il de la plus courte ?

Andrei et Penny

.