Introduction

Le flambement des colonnes est un sujet curieux et unique. C’est peut-être le seul domaine de la mécanique des structures dans lequel la défaillance n’est pas liée à la résistance du matériau.Une analyse de flambement de colonne consiste à déterminer la charge maximale qu’une colonne peut supporter avant de s’effondrer. Mais pour les colonnes longues, l’effondrement n’a rien à voir avec le rendement du matériau. Il est au contraire régi par la rigidité de la colonne, à la fois matérielle et géométrique.
Cette page va dériver les équations standard du flambement des colonnes en utilisant deux approches.Elle couvrira d’abord le développement habituel des équations,c’est-à-dire la théorie du flambement d’Euler. Il s’agit de la dérivation que l’on trouve dans les manuels et qui est présentée dans les cours d’ingénierie. Mais je ne l’ai jamais aimée. Non pas parce qu’elle est incorrecte (elle est correcte), mais parce que je ne pense pas qu’elle présente de manière satisfaisante les mécanismes physiques qui régissent le processus de flambage. C’est pourquoi une seconde dérivation des équations de flambement sera également présentée.
Curieusement, les objets sont appelés colonnes lorsqu’ils sont chargés axialement en compression, comme c’est le cas ici, mais ils sont appelés poutres lorsqu’ils sont chargés transversalement.Néanmoins, la théorie de la flexion des poutres est centrale pour les analyses de flambement des colonnes, il est donc recommandé au lecteur de revoir cette page sur la flexion des poutres.

Théorie du flambement d’Euler

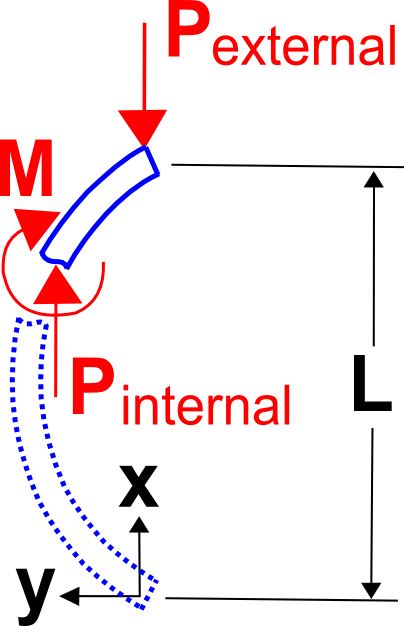
La théorie du flambement d’Euler est la théorie classique présentée dans les manuels et les salles de classe. Elle commence simplement en notant que le moment de flexion interne dans une colonne chargée et déformée est \(-P \, y\) où \(P\) est la charge de compression et \(y\) est la déviation de la colonne. Insérez donc \(-P \, y\) dans pour \(M\) dans l’équation de flexion de la poutre, \( E \, I \, y » = M \).

Cela produit l’équation différentielle suivante

qui a pour solution

où \(A\) et \(B\) sont des constantes déterminées à partir des conditions aux limites.
Les conditions aux limites sont \(y = 0\) à \(x = 0\) et \(x = L\).
La première condition aux limites, \(y = 0\) à \(x = 0\), conduit à la conclusion que \(B = 0\). Et cela laisse

C’est jusque là, tout va bien. Mais c’est à ce stade que la dérivation classique tend à laisser de côté l’intuition physique pour devenir ouvertement mathématique…
Les choses deviennent très intéressantes avec la 2ème condition aux limites car, comme nous allons le voir, elle ne conduit pas à la détermination de la constante inconnue, \(A\). Pour s’en rendre compte, insérez la seconde condition limite comme suit.

\N
Il y a fondamentalement deux possibilités ici. Dans le premier cas, \(A = 0\), mais c’est ennuyeux car cela conduit au résultat que tous les déplacements sont nuls. Il s’agit simplement de la solution sans flambage. Avant que la colonne ne se déforme, ses déplacements latéraux sont simplement nuls.
Le deuxième cas est le plus intéressant, et celui qui est directement lié au flambage de la colonne. La deuxième méthode pour satisfaire la condition aux limites est de noter que \(\sin(\pi) = 0\). Par conséquent, la façon de satisfaire la condition aux limites est d’exiger que l’argument dans l’équation, \(\left( \sqrt{P \over E \, I}} \ ; L \right)\) doit être égal à \(\pi\).Ce faisant, on obtient

\
et la résolution de \(P\) donne

C’est le résultat classique de la théorie de flambage d’Euler. Il donne la valeur critique de la charge \(P\), appelée \(P_{cr}\), au-delà de laquelle, la colonne se déforme.
Ce résultat est parfaitement légitime. Cependant, comme cela devrait être évident maintenant, il est très mathématique dans la nature, et fournit peu de perspicacité physique en conséquence. La dérivation à venir ci-dessous présentera une méthode alternative pour arriver à la même équation qui, selon moi, fournit une connexion physique beaucoup plus directe au processus de flambage que la dérivation ci-dessus.

Buckling vs Yielding

Comme indiqué au début, l’analyse classique du flambement est indépendante de la limite élastique d’un matériau. Cela est évident dans la dérivation ci-dessus car à aucun moment la contrainte ou la déformation n’a été discutée ou comparée à la résistance d’un matériau.
Mais en fait, les considérations relatives à la limite d’élasticité ne doivent jamais être totalement ignorées. Une fois que l’on a obtenu une estimation de \(P_{cr}\) à partir de l’équation ci-dessus, il faut toujours la diviser par l’aire de la section transversale de la colonne, \(A\), pour obtenir une contrainte

et comparer cette valeur à la limite d’élasticité du matériau pour déterminer si une déformation se produira avant le flambage. Ceci est critique pour les colonnes courtes car elles ont des valeurs \(P_{cr}\) intrinsèquement élevées car \(L^2\) est au dénominateur de l’équation de flambement.

Contraintes d’extrémité dans le flambement

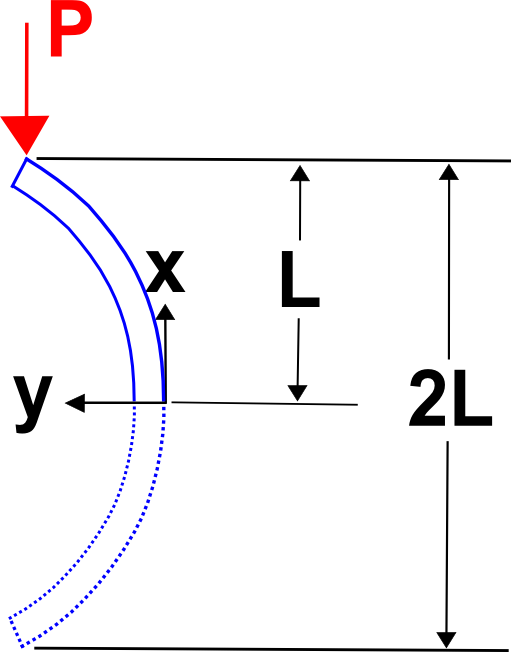
Bien que ce ne soit pas le sujet de cette page, il est important de reconnaître que les contraintes d’extrémité sont essentielles aux analyses de flambement car elles modifient la valeur de \(P_{cr}\). Par exemple, considérez que la charge de flambement critique de la colonne illustrée ici est donnée par
\
Notez que cette valeur est 1/4 de celle donnée dans l’équation précédente pour \(P_{cr}\).Mais il est facile de voir pourquoi. Le croquis montre que la condition de flambage ici est exactement équivalente au flambage d’une colonne de deux fois la longueur et ayant les mêmes conditions aux limites que dans la dérivation ci-dessus. Et cela conduit à
\

Dérivation de flambement basée sur la physique

Cette section présentera une méthode alternative de détermination des charges critiques de flambement qui, je crois, est plus intuitive physiquement que la théorie classique de flambement d’Euler. Sa caractéristique principale est la comparaison entre le moment de flexion interne résultant de la distribution interne des contraintes et le moment de flexion externe résultant de la charge appliquée à la colonne. (La phrase précédente est critique.)
Cette approche reprend approximativement là où il a été noté précédemment que l’approche classique d’Euler devient ouvertement mathématique. La première étape consiste à supposer une forme déformée. Nous savons que \(y = 0\) aux deux extrémités de la colonne, et que la forme suit une fonction \(\sin()\) basée sur l’équation différentielle ci-dessus. Le choix le plus logique est donc
\
où \(\delta_{max}\) est le déplacement latéral au point central de la colonne. Sa valeur est inconnue, mais on sait qu’il est plus grand au point médian qu’en tout autre point de la colonne, d’où l’indice \(max\). Le choix de \(\pi x / L\) comme argument de la fonction \(\sin()\) garantit que les déplacements sont nuls en \(x = 0\) et \(x = L\). (Nous parlerons des autres formes supposées sous peu.)

Si vous vous interrogez sur le terme \(\sqrt{P/EI}\) de la fonction \(\sin()\) de la solution d’Euler précédente, ne vous en faites pas. Il provient de la solution de l’équation différentielle, mais nous prétendons ici ne rien savoir des détails de cette solution (alerte aux exceptions !). Nous avons seulement besoin d’une fonction qui puisse ressembler à une colonne courbée avec des déplacements nuls à ses extrémités. L’utilisation de \(\sin ( {\pi x \over L} )\) permet d’y parvenir.
L’alerte à l’exception est présente ci-dessus parce que nous profitons en fait d’un élément de connaissance sur l’analyse précédente. Il s’agit du fait que les fonctions trigonométriques sont les solutions de l’équation différentielle.Par conséquent, les sinus et les cosinus doivent être utilisés chaque fois que possible pour décrire les formes déformées car ils conduiront aux estimations les plus précises de \(P_{cr}\).

Rappellez-vous de la théorie de la flexion des poutres que le moment de flexion, \(M\), est lié à la déflexion du poteau par
\
Bien que cela ne soit pas critique, il est utile de se rappeler que cette relation est issue du calcul du moment dans la section transversale dû à la distribution de la contrainte. La relation montre que nous avons besoin de cette dérivée seconde de la fonction de déplacement supposée.

\
C’est le moment de flexion interne de la colonne dû à la distribution de la contrainte en son sein, qui est à son tour due au fait que la colonne est courbée.
Vient ici une pensée importante…. Ce moment de flexion peut être considéré comme la résistance interne de la colonne à la flexion, ou la force avec laquelle elle essaie de se redresser.
La prochaine étape simple est d’égaler ce moment de flexion interne résistif à celui résultant de la charge externe. Cette quantité est simplement \(M = -P \, y(x)\). En égalisant les deux, on obtient
\
Il n’est pas difficile de voir à ce stade que cette approche conduit à la même expression pour \(P_{cr}\) que la théorie classique du flambement d’Euler.Mais en cours de route, il a fourni beaucoup plus de compréhension du processus physique de flambement que la première théorie. A savoir…

1. Nous sommes arrivés à cette relation en mettant en équation le moment de flexion interne (dû aux contraintes internes résultant de la flexion de la colonne)et le moment de flexion externe résultant de la charge externe, \(P\).Il devrait être clair que le flambement se produit lorsque \(P\) est assez grand pour satisfaire l’équation. Toute valeur inférieure, et \(P \, y(x)\) sera inférieure au « moment de flexion résistant. »
2. Le fait que \(y(x)\) apparaisse des deux côtés de l’équation, et sera donc annulé, signifie que lorsque le flambement se produit, il le fait simultanément sur toute la longueur de la colonne. (Un résultat fascinant qui n’est pas évident dans la théorie d’Euler.)

De toute façon, en annulant \(y(x)\) des deux côtés de l’équation, on obtient
\
de nouveau, mais avec beaucoup plus de perspicacité physique cette fois.

Exemple d’extrémité fixe

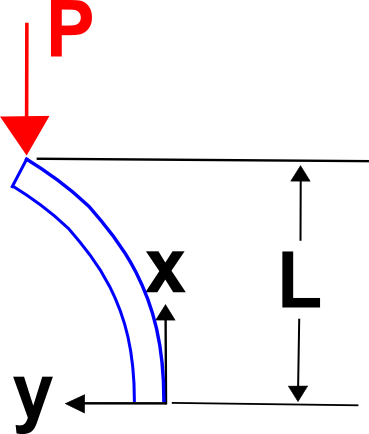
Cette fois, supposez une forme déformée de

Calculez le moment de flexion dû à cela.

Le moment de flexion dû à la charge externe est \(M = P ( \delta_{max} – y(x) )\). En mettant ces deux éléments en équation et en simplifiant, on obtient le résultat connu.
\

Exemple d’extrémité fixe avec une forme supposée différente

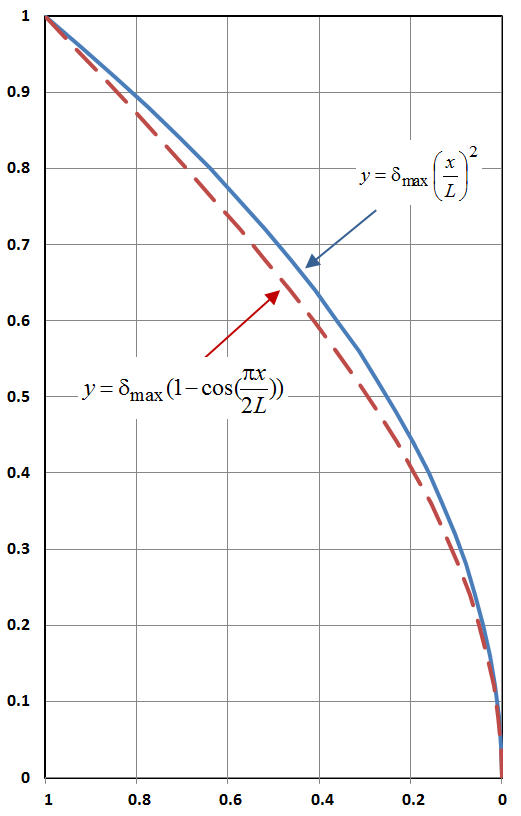.Flexion de la colonne

Cet exemple démontrera que d’autres fonctions peuvent être supposées pour la forme déformée de la colonne, et que la formule résultante pour \(P_{cr}\) ne sera pas significativement différente de la solution exacte.
Cette fois, supposez une forme déformée de

Calculez le moment de flexion dû à celle-ci.

Le moment de flexion dû à la charge externe reste \(M = P ( \delta_{max} – y(x) )\). En mettant ces deux valeurs en équation, on obtient

Il est clair, d’après cette équation, que la valeur minimale de \(P\) se produira à \(x = 0\)car c’est à ce moment que \(y(x)\) est un minimum (zéro, en fait) et donc\((\delta_{max} – y(x))\) est un maximum. En fixant \(y(x)\) à zéro et en annulant\(\delta_{max}\) des deux côtés, on obtient
\

Ce résultat n’est évidemment pas égal à la solution exacte ci-dessus. La différence est que la solution exacte contient \(\pi^2 / 4 = 2,467\), alors que cette solution approximative en contient 2, soit une différence de 23%. C’est significatif, mais pas aussi important que, disons, un facteur de 2, ou un ordre de grandeur. Notez également que la solution approximative est conservatrice puisqu’elle donne une charge critique de flambage inférieure à celle de la solution exacte.
Il est intéressant de noter que cette solution basée sur la forme quadratique, a conduit à une charge critique de flambage plus faible et à une concentration de la rupture par flambage à la base de la colonne, \(x = 0\).En revanche, la solution exacte constituée de la fonction trigonométrique, a produit une tendance égale au flambage sur toute la longueur de la colonne, et une \(P_{cr}\) correspondante plus élevée.
Un facteur clé ici est que la forme déformée quadratique supposée n’est pas une solution exacte de l’équation différentielle gouvernante (bien qu’elle en soit proche). Les fonctions trigonométriques le sont.