Contexte
La cryptographie à courbes elliptiques (ECC) est une approche de la cryptographie à clé publique, basée sur la structure algébrique des courbes elliptiques sur des champs finis. ECC nécessite une clé plus petite par rapport à la cryptographie non-ECC pour fournir une sécurité équivalente (une sécurité ECC de 256 bits a une sécurité équivalente atteinte par la cryptographie RSA de 3072 bits).
Pour mieux comprendre la cryptographie à courbes elliptiques, il est très important de comprendre les bases de la courbe elliptique. Une courbe elliptique est une courbe algébrique planaire définie par une équation de la forme
![]()
Où ‘a’ est le coefficient de x et ‘b’ est la constante de l’équation
La courbe est non-singulière ; c’est-à-dire que son graphe ne comporte pas de cuspides ou d’auto-intersections (lorsque la caractéristique du champ des coefficients est égale à 2 ou 3).
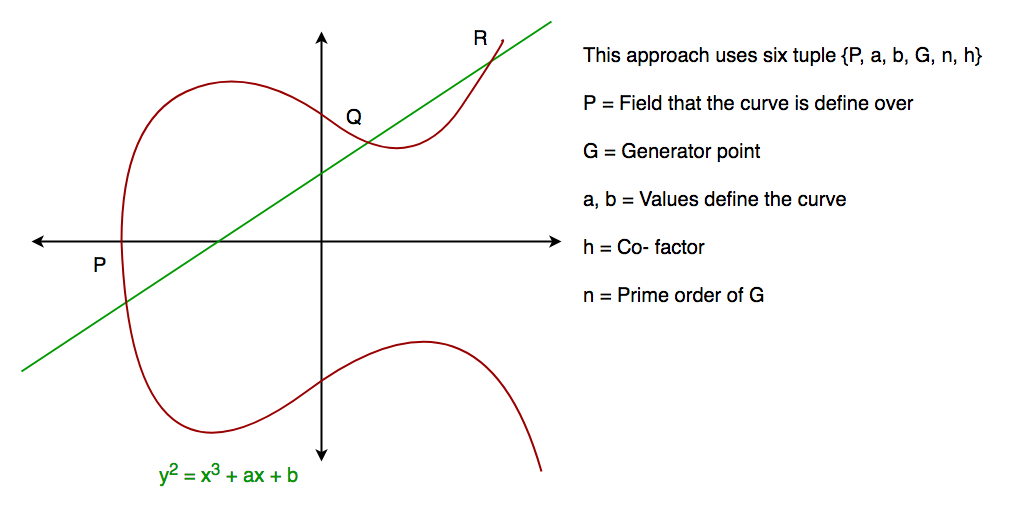
En général, une courbe elliptique ressemble à celle présentée ci-dessous. Les courbes elliptiques pourraient se croiser presque 3 points lorsqu’une ligne droite est tracée en coupant la courbe. Comme nous pouvons le voir, la courbe elliptique est symétrique par rapport à l’axe des x, cette propriété joue un rôle clé dans l’algorithme.
Algorithme de Diffie-Hellman
L’algorithme de Diffie-Hellman est utilisé pour établir un secret partagé qui peut être utilisé pour des communications secrètes tout en échangeant des données sur un réseau public en utilisant la courbe elliptique pour générer des points et obtenir la clé secrète en utilisant les paramètres.
- Pour des raisons de simplicité et de mise en œuvre pratique de l’algorithme, nous ne considérerons que 4 variables un nombre premier P et G (une racine primitive de P) et deux valeurs privées a et b.
- P et G sont tous deux des nombres accessibles au public. Les utilisateurs (disons Alice et Bob) choisissent les valeurs privées a et b et ils génèrent une clé et l’échangent publiquement, la personne opposée a reçu la clé et à partir de cela génère une clé secrète après quoi ils ont la même clé secrète pour chiffrer.
Explication étape par étape
| Alice | Bob |
|---|---|
| Clés publiques disponibles = P, G | Clefs publiques disponibles = P, G |
| Clé privée sélectionnée = a | Clé privée sélectionnée = b |
Clé générée .
|
Clé générée =
|
| L’échange des clés générées a lieu | |
| Clé reçue = y | Clé reçue = x |
|
Clé secrète générée =
|
Clé secrète générée =
. |
|
Algébriquement, on peut montrer que
. |
|
| Les utilisateurs disposent maintenant d’une clé secrète symétrique pour chiffrer | |
Exemple
Step 1: Alice and Bob get public numbers P = 23, G = 9Step 2: Alice selected a private key a = 4 and Bob selected a private key b = 3Step 3: Alice and Bob compute public valuesAlice: x =(9^4 mod 23) = (6561 mod 23) = 6 Bob: y = (9^3 mod 23) = (729 mod 23) = 16Step 4: Alice and Bob exchange public numbersStep 5: Alice receives public key y =16 and Bob receives public key x = 6Step 6: Alice and Bob compute symmetric keys Alice: ka = y^a mod p = 65536 mod 23 = 9 Bob: kb = x^b mod p = 216 mod 23 = 9Step 7: 9 is the shared secret.
Mise en œuvre :
.
#include<stdio.h>#include<math.h>longlongintpower(longlong
inta, longlongintb,
longlongintP) { if(b == 1). returna; else return(((longlongint)pow(a, b)) % P); }.
intmain()
{ longlongintP, G, x, a, y, b, ka, kb;
P = 23;
printf("The value of P : %lld\n", P);
G = 9; iv
printf("The value of G : %lld\n\n", G); a = 4; printf("The private key a for Alice : %lld\n", a);
x = power(G, a, P);
b = 3; printf("The private key b for Bob : %lld\n\n", b);
y = power(G, b, P); . ka = power(y, a, P); kb = power(x, b, P);
printf("Secret key for the Alice is : %lld\n", ka); printf("Secret Key for the Bob is : %lld\n", kb); return0; }.
.
.
.
fromrandom importrandint
if__name__ =='__main__': . P =23
. G
=9
print('The Value of P is :%d'%(P)) print('The Value of G is :%d'%(G))
a =4 print('The Private Key a for Alice is :%d'%(a)) x =int(pow(G,a,P)) b =3
print('The Private Key b for Bob is :%d'%(b))
y =int
(pow(G,b,P))
ka =int(pow(y,a,P))
.
kb =int(pow(x,b,P)) . print('Secret key for the Alice is : %d'%(ka))
print('Secret Key for the Bob is : %d'%(kb))
Sortie
The value of P : 23The value of G : 9The private key a for Alice : 4The private key b for Bob : 3Secret key for the Alice is : 9Secret Key for the Bob is : 9
Cet article est une contribution de Souvik Nandi. Si vous aimez GeeksforGeeks et souhaitez contribuer, vous pouvez également écrire un article en utilisant contribute.GeeksforGeeks.org ou envoyer votre article par courrier à [email protected]. Voyez votre article apparaître sur la page principale de GeeksforGeeks et aidez d’autres Geeks.
Veuillez écrire des commentaires si vous trouvez quelque chose d’incorrect, ou si vous voulez partager plus d’informations sur le sujet abordé ci-dessus.