قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).
Définition
La loi de Bragg fournit la condition pour qu’une onde plane soit diffractée par une famille de plans de treillis :
2 d sin θ = n λ
où d est l’espacement interplanaire, θ l’angle entre le vecteur d’onde de l’onde plane incidente, ko, et les plans du réseau, λ sa longueur d’onde et n est un nombre entier, l’ordre de la réflexion. Elle est équivalente à la condition de diffraction dans l’espace réciproque et aux équations de Laue.
Dérivation directe de la loi de Bragg
- Réflexion à partir du premier plan
Les ondes diffusées seront en phase quelle que soit la distribution des diffuseurs ponctuels dans le premier plan si l’angle du vecteur d’onde réfléchi, kh, est également égal à θ. C’est la loi de réflexion de Snell-Descartes.
- Réflexion à partir du second plan
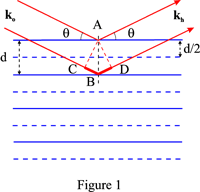
Puisque la phase des ondes réfléchies est indépendante de la position du diffuseur ponctuel dans le plan, la différence de phase entre les ondes réfléchies par deux plans successifs du réseau est obtenue en choisissant arbitrairement un point de diffusion, A, sur le premier plan et un point de diffusion, B, sur le second plan de telle sorte que AB soit normal aux plans. Si C et D sont les projections de A sur les vecteurs d’onde incidente et réfléchie passant par B, il ressort de la figure 1 que la différence de parcours entre les ondes réfléchies en A et B, respectivement, est :
CB + BD = 2d sin θ
et que les deux ondes seront en phase si cette différence de parcours est égale à nλ où n est un entier.
- Réflexion sur le troisième plan, etc.
Si la relation de Bragg est satisfaite pour les deux premiers plans, les ondes réfléchies avec le vecteur d’onde kh seront en phase pour tous les plans de la famille.
Ordre de la réflexion
La loi de Bragg peut aussi s’écrire :
2 (d/n) sin θ = λ.
On peut alors dire qu’une réflexion de Bragg d’ordre n sur une famille de plans de réseau d’ordre n est équivalente à une réflexion d’ordre 1 sur une famille de plans fictifs, ou imaginaires, d’espacement de réseau
d_{hkl} = d/n.
Cette famille fictive est associée au vecteur réciproque du réseau OH où OH = n/d = 1/d_{hkl}. Les indices de réflexion sont hkl. Par exemple, les lignes horizontales en pointillés de la figure 1 correspondent aux plans fictifs associés au second ordre, n = 2.
Conditions de réflexion
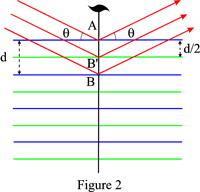
S’il existe un plan de glissement ou un axe de vis normal aux plans du réseau, l’espacement des plans réfléchissants réels est de d/2 pour un plan de glissement et de (d p/q) pour un axe de vis qp. La loi de Bragg doit alors s’écrire :
2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ
pour un plan de glissement et
pour un axe de vis qp.
2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ
pour un axe de vis qp.
Les réflexions d’ordre impair pour un plan de glissement et d’ordre différent de (q/p)n pour un axe de vis sont alors absentes. On parle d’absences systématiques liées à la présence de composantes de glissement ou de vis.
À titre d’exemple, la figure 2 montre le cas d’un axe de vis 21 : les plans réfléchissants sont les plans bleus et les plans verts déduits de ces derniers par l’action de l’axe de vis. Les réflexions d’ordre impair seront systématiquement absentes.
Influence de la déformation
Une déformation qui laisse une famille de plans de réseau (hkl) non déformée et son espacement de réseau d inchangé n’affectera pas l’angle de Bragg des réflexions kkl, par ex.par exemple, les plans de réseau parallèles à une vis dislocations.
Histoire
Bragg (1890-1971) a présenté sa dérivation de la condition de réflexion lors d’une réunion de la Cambridge Philosophical Society le 11 novembre 1912. Son article a été publié en 1913. Pour plus de détails, voir P. P. Ewald (1962), 50 ans de diffraction des rayons X, Utrecht : IUCr/Oosthoek, section 5, p. 64 et A. Authier (2013), The Early Days of X-ray Diffraction, Oxford : IUCr/Oxford University Press, section 6.11, p. 120.
Voir aussi
- Équations de Laue
.