Taux d’erreur par famille > Holm-.Bonferroni Method

Vous pouvez d’abord lire cet article : Taux d’erreur par famille.

Qu’est-ce que la méthode de Holm-Bonferroni ?

La méthode de Holm-Bonferroni (également appelée procédure séquentielle de Bonferroni de Holm) est une façon de traiter les taux d’erreur par famille (FWER) pour les tests d’hypothèses multiples. Il s’agit d’une modification de la correction de Bonferroni. La correction de Bonferroni réduit la possibilité d’obtenir un résultat statistiquement significatif (c’est-à-dire une erreur de type I) lors de la réalisation de tests multiples. Bien que la correction de Bonferroni soit simple à calculer, elle souffre d’un manque de puissance statistique. La méthode de Holm-Bonferroni est également assez simple à calculer, mais elle est plus puissante que le Bonferroni en une seule étape.

Formule

La formule pour calculer le Holm-Bonferroni est: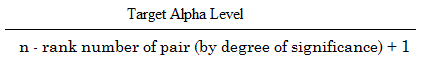

Où:

• Niveau alpha cible = niveau alpha global (généralement .05),
• n = nombre de tests.

L’exemple suivant montre comment la formule fonctionne.

Exemple

Question : Utilisez la méthode de Holm-Bonferroni pour tester les quatre hypothèses suivantes et leurs valeurs p associées à un niveau alpha de 0,05 :

• H1 = 0.01.
• H2 = 0,04
• H3 = 0,03
• H4 = 0,005

Note : nous connaissons déjà les valeurs p associées à chaque hypothèse. Si vous ne connaissez pas les valeurs p, effectuez un test pour chaque hypothèse avant de tenter d’ajuster le FWER à l’aide de la méthode de Holm-Bonferroni.

Étape 1 : ordonnez les valeurs p de la plus petite à la plus grande :

• H4 = 0.005
• H1 = 0,01
• H3 = 0,03
• H2 = 0,04

Étape 2 : Travailler la formule de Holm-Bonferroni pour le premier rang :
HB = Cible α / (n – rang + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Étape 3 : Comparez la valeur p du premier rang (la plus petite) de l’étape 1 au niveau alpha calculé à l’étape 2 :
La plus petite valeur p, à l’étape 1 (H4 = 0.005) < Niveau alpha à l’étape 2 (.0125).
Si la valeur p est plus petite, rejetez l’hypothèse nulle pour ce test individuel.

La valeur p de 0,005 est inférieure à 0,0125, donc l’hypothèse nulle pour H4 est rejetée.

Etape 4 : Répétez la formule HB pour le deuxième rang .
HB = Cible α / (n – rang + 1)
HB = 0,05 / 4 – 2 + 1 = 0,05 / 3 = 0,0167

Étape 5 : Comparer le résultat de la formule HB de l’étape 4 à la valeur p du deuxième rang :
Valeur p de deuxième rang, à l’étape 1 (H1 = 0,01) < Niveau alpha à l’étape 2 (,0167).
La valeur p de 0,01 est inférieure à 0,0167, donc l’hypothèse nulle pour H1 est également rejetée.

Étape 6 : Répétez la formule HB pour le troisième rang.
HB = Cible α / (n – rang + 1)
HB = ,05 / 4 – 3 + 1 = ,05 / 2 = ,025

Étape 7 : Comparez le résultat de la formule HB de l’étape 6 à la valeur p du troisième rang :
Valeur p de troisième rang, à l’étape 1 (H3 = 0,03) > Niveau alpha à l’étape 6 (,025).
La valeur p de 0,03 est supérieure à 0,025, l’hypothèse nulle pour H3 n’est donc pas rejetée.

Le test s’arrête lorsque vous atteignez la première hypothèse non rejetée. Toutes les hypothèses suivantes sont non significatives (c’est-à-dire non rejetées).

Référence:
Holm, S. 1979. Une procédure simple de test multiple réjectif séquentiel. Scandinavian Journal of Statistics 6:65-70

——————————————————————————

Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !