Un exemple de backpropagation étape par étape - Matt Mazur

Contexte

La backpropagation est une méthode courante pour former un réseau neuronal. Il ne manque pas d’articles en ligne qui tentent d’expliquer le fonctionnement de la rétropropagation, mais rares sont ceux qui incluent un exemple avec des chiffres réels. Ce post est ma tentative d’expliquer comment cela fonctionne avec un exemple concret auquel les gens peuvent comparer leurs propres calculs afin de s’assurer qu’ils comprennent correctement la rétropropagation.

Backpropagation en Python

Vous pouvez jouer avec un script Python que j’ai écrit et qui implémente l’algorithme de rétropropagation dans ce repo Github.

Visualisation de la rétropropagation

Pour une visualisation interactive montrant un réseau neuronal au fur et à mesure de son apprentissage, consultez ma visualisation de réseau neuronal.

Ressources supplémentaires

Si vous trouvez ce tutoriel utile et que vous voulez continuer à apprendre sur les réseaux neuronaux, l’apprentissage automatique et l’apprentissage profond, je vous recommande vivement de consulter le nouveau livre d’Adrian Rosebrock, Deep Learning for Computer Vision with Python. J’ai vraiment apprécié le livre et j’aurai bientôt une critique complète.

Overview

Pour ce tutoriel, nous allons utiliser un réseau neuronal avec deux entrées, deux neurones cachés, deux neurones de sortie. De plus, les neurones cachés et de sortie comprendront un biais.

Voici la structure de base :

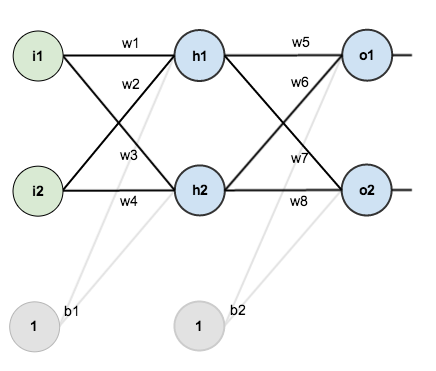
réseau_neural (7)

Afin d’avoir quelques chiffres sur lesquels travailler, voici les poids initiaux, les biais et les entrées/sorties d’entraînement :

réseau_neural (9)

Le but de la rétropropagation est d’optimiser les poids afin que le réseau neuronal puisse apprendre à mettre correctement en correspondance des entrées arbitraires et des sorties.

Pour le reste de ce tutoriel, nous allons travailler avec un seul ensemble d’apprentissage : étant donné les entrées 0,05 et 0,10, nous voulons que le réseau neuronal produise 0,01 et 0,99.

Le passage en avant

Pour commencer, voyons ce que le réseau neuronal prédit actuellement étant donné les poids et les biais ci-dessus et les entrées de 0,05 et 0,10. Pour ce faire, nous allons faire passer ces entrées dans le réseau.

Nous calculons l’entrée nette totale de chaque neurone de la couche cachée, nous écrasons l’entrée nette totale à l’aide d’une fonction d’activation (ici, nous utilisons la fonction logistique), puis nous répétons le processus avec les neurones de la couche de sortie.

L’entrée nette totale est également appelée juste entrée nette par certaines sources.

Voici comment nous calculons l’entrée nette totale pour $h_1$ :

$net_{h1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1$

$net_{h1} = 0.15 * 0.05 + 0.2 * 0.1 + 0.35 * 1 = 0.3775$

Nous l’écrasons ensuite à l’aide de la fonction logistique pour obtenir la sortie de $h_1$ :

$out_{h1} = \frac{1}{1+e^{-net_{h1}} = \frac{1}{1+e^{-0.3775}} = 0,593269992$

En effectuant le même processus pour $h_2$ on obtient :

$out_{h2} = 0.596884378$

Nous répétons ce processus pour les neurones de la couche de sortie, en utilisant les sorties des neurones de la couche cachée comme entrées.

Voici la sortie pour $o_1$ :

$net_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1$

$net_{o1} = 0,4 * 0,593269992 + 0,45 * 0,596884378 + 0,6 * 1 = 1.105905967$

$out_{o1} = \frac{1}{1+e^{-net_{o1}} = \frac{1}{1+e^{-1.105905967}} = 0,75136507$

Et en effectuant le même processus pour $o_2$ on obtient :

$out_{o2} = 0.772928465$

Calcul de l’erreur totale

Nous pouvons maintenant calculer l’erreur pour chaque neurone de sortie en utilisant la fonction d’erreur au carré et les additionner pour obtenir l’erreur totale :

$E_{total} = \sum \frac{1}{2}(cible - sortie)^{2}$

Certaines sources désignent la cible comme l’idéal et la sortie comme le réel.

La $\frac{1}{2}$ est incluse afin que l’exposant soit annulé lorsque nous différencierons plus tard. Le résultat est finalement multiplié par un taux d’apprentissage de toute façon, donc cela n’a pas d’importance que nous introduisions une constante ici .

Par exemple, la sortie cible pour $o_1$ est 0.01 mais la sortie du réseau neuronal est de 0,75136507, donc son erreur est:

$E_{o1} = \frac{1}{2}(target_{o1} - out_{o1})^{2} = \frac{1}{2}(0.01 - 0,75136507)^{2} = 0,274811083$

Répéter ce processus pour $o_2$ (en se rappelant que la cible est 0.99), nous obtenons :

$E_{o2} = 0,023560026$

L’erreur totale pour le réseau neuronal est la somme de ces erreurs :

$E_{total} = E_{o1} + E_{o2} = 0,274811083 + 0,023560026 = 0,298371109$

La rétropropagation

Notre objectif avec la rétropropagation est de mettre à jour chacun des poids du réseau afin qu’ils fassent en sorte que la sortie réelle soit plus proche de la sortie cible, minimisant ainsi l’erreur pour chaque neurone de sortie et le réseau dans son ensemble.

Couche de sortie

Considérons $w_5$ . Nous voulons savoir de combien un changement dans $w_5$ affecte l’erreur totale, alias $\frac{\partial E_{total}}{\partial w_{5}}$ .

$\frac{\partial E_{total}}{\partial w_{5}}$ se lit comme « la dérivée partielle de $E_{total}$ par rapport à $w_{5}$ « . On peut aussi dire « le gradient par rapport à $w_{5}$ « .

En appliquant la règle de la chaîne, nous savons que :

$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$

Visuellement, voici ce que nous faisons:

sortie_1_backprop (4)

Nous devons déterminer chaque élément de cette équation.

Premièrement, de combien l’erreur totale change-t-elle par rapport à la sortie ?

$E_{total} = \frac{1}{2}(target_{o1} - out_{o1})^{2}. + \frac{1}{2}(cible_{o2} - out_{o2})^{2}$

$\frac{\partial E_{total}}{\partial out_{o1}} = 2 * \frac{1}{2}(cible_{o1} - out_{o1})^{2 - 1} * -1 + 0$

$\frac{\partial E_{total}{\partial out_{o1}} = -(target_{o1} - out_{o1}) = -(0.01 - 0.75136507) = 0.74136507$

$-(cible - out)$ est parfois exprimé par $out - cible$

Lorsque l’on prend la dérivée partielle de l’erreur totale par rapport à $out_{o1}$ , la quantité $\frac{1}{2}(target_{o2} - out_{o2})^{2}$ devient nulle car $out_{o1}$ ne l’affecte pas ce qui signifie que nous prenons la dérivée d’une constante qui est nulle.

Suite, de combien varie la sortie de $o_1$ par rapport à son entrée nette totale ?

La dérivée partielle de la fonction logistique est la sortie multipliée par 1 moins la sortie :

$out_{o1} = \frac{1}{1+e^{-net_{o1}}$

$\frac{\partial out_{o1}{\partial net_{o1}} = out_{o1}(1 - out_{o1}) = 0.75136507(1 - 0,75136507) = 0,186815602$

Enfin, de combien varie l’apport net total de $o1$ par rapport à $w_5$ ?

$net_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1$

$\frac{\partial net_{o1}}{\partial w_{5} = 1 * out_{h1} * w_5^{(1 - 1)} + 0 + 0 = out_{h1} = 0,593269992$

Mise en commun:

$\frac{\partial E_{total}{\partial w_{5}} = \frac{\partial E_{total}{\partial out_{o1}} * \frac{\partial out_{o1}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$

$\frac{\partial E_{total}}{\partial w_{5}} = 0,74136507 * 0,186815602 * 0,593269992 = 0.082167041$

Vous verrez souvent ce calcul combiné sous la forme de la règle du delta :

$\frac{\partial E_{total}}{\partial w_{5}} = -(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1}) * out_{h1}$

Alternativement, nous avons $\frac{\partial E_{total}}{\partial out_{o1}}$ et $\frac{\partial out_{o1}}{\partial net_{o1}}$ qui peut s’écrire $\frac{\partial E_{total}}{\partial net_{o1}}$ , alias $\delta_{o1}$ (la lettre grecque delta) alias le nœud delta. Nous pouvons l’utiliser pour réécrire le calcul ci-dessus :

$\delta_{o1} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} = \frac{\partial E_{total}}{\partial net_{o1}$

$\delta_{o1} = -(cible_{o1} - out_{o1}) * out_{o1}(1 - out_{o1})$

Ainsi :

$\frac{\partial E_{total}}{\partial w_{5}} = \delta_{o1} out_{h1}$

Certaines sources extraient le signe négatif de $\delta$ de sorte qu’il s’écrirait comme :

$\frac{\partial E_{total}}{\partial w_{5}} = -\delta_{o1} out_{h1}$

Pour diminuer l’erreur, nous soustrayons ensuite cette valeur du poids actuel (éventuellement multiplié par un certain taux d’apprentissage, eta, que nous fixerons à 0.5):

$w_5^{+} = w_5 - \eta * \frac{\partial E_{total}}{\partial w_{5}} = 0,4 - 0,5 * 0,082167041 = 0.35891648$

Certaines sources utilisent $\alpha$ (alpha) pour représenter le taux d’apprentissage, d’autres utilisent $\eta$ (eta), et d’autres encore $\epsilon$ (epsilon).

Nous pouvons répéter ce processus pour obtenir les nouveaux poids $w_6$ $w_7$ , et $w_8$ :

$w_6^{+} = 0.408666186$

$w_7^{+} = 0.511301270$

$w_8^{+} = 0,561370121$

Nous effectuons les mises à jour réelles dans le réseau neuronal après avoir obtenu les nouveaux poids menant aux neurones de la couche cachée (c’est-à-dire que nous utilisons les poids originaux, et non les poids mis à jour, lorsque nous poursuivons l’algorithme de rétropropagation ci-dessous).

Couche cachée

Après, nous allons continuer la passe en arrière en calculant de nouvelles valeurs pour $w_1$ $w_2$ $w_3$ , et $w_4$ .

Voilà ce qu’il faut comprendre :

$\frac{\partial E_{total}{\partial w_{1}} = \frac{\partial E_{total}}{\partial out_{h1}} * \frac{\partial out_{h1}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

Visuellement :

nn-calcul

Nous allons utiliser un processus similaire à celui de la couche de sortie, mais légèrement différent pour tenir compte du fait que la sortie de chaque neurone de la couche cachée contribue à la sortie (et donc à l’erreur) de plusieurs neurones de sortie. Nous savons que $sortie_{h1}$ affecte à la fois la $sortie_{o1}$ et la $sortie_{o2}$ ; donc le $\frac{\partial E_{total}}{\partial out_{h1}}$ doit prendre en compte son effet sur les deux neurones de sortie :

$\frac{\partial E_{total}{\partial out_{h1}} = \frac{\partial E_{o1}{\partial out_{h1}} + \frac{\partial E_{o2}{\partial out_{h1}}$

En commençant par $\frac{\partial E_{o1}}{\partial out_{h1}}$ :

$\frac{\i1}partiel E_{o1}}{\i1}partiel out_{h1}} = \frac{\i1}partiel E_{o1}}{\i1}partiel net_{o1}} * \frac{\partial net_{o1}}{\partial out_{h1}}$

Nous pouvons calculer $\frac{\partial E_{o1}}{\partial net_{o1}}$ en utilisant les valeurs que nous avons calculées précédemment :

${\frac{\i1}E_{\i1}partiel net{\i1}} = \frac{\i1}E_{\i1}partiel out{\i1}}{\i1}partiel out{\i}} * \frac{\partial out_{o1}}{\partial net_{o1}} = 0.74136507 * 0.186815602 = 0.138498562$

Et $\frac{\partial net_{o1}}{\partial out_{h1}}$ est égal à $w_5$ :

$net_{o1} = w_5 * out_{h1} + w_6 * out_{h2} + b_2 * 1$

$\frac{\partial net_{o1}}{\partial out_{h1}} = w_5 = 0.40$

Les brancher :

${\frac{\c}{\c} E_{o1}}{\c} out_{h1}} = \frac{\c}{\c} net_{o1}}{\c} * \frac{\partial net_{o1}}{\partial out_{h1}} = 0.138498562 * 0.40 = 0.055399425$

En suivant le même processus pour $\frac{\partial E_{o2}}{\partial out_{h1}}$ , on obtient:

$\frac{\partial E_{o2}}{\partial out_{h1}} = -0.019049119$

Donc:

$\frac{\partial E_{total}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}{\partial out_{h1}} = 0.055399425 + -0.019049119 = 0.036350306$

Maintenant que nous avons $\frac{\partial E_{total}}{\partial out_{h1}}$ , nous devons déterminer $\frac{\partial out_{h1}}{\partial net_{h1}}$ et ensuite $\frac{\partial net_{h1}}{\partial w}$ pour chaque poids :

$out_{h1} = \frac{1}{1+e^{-net_{h1}}$

$\frac{\partial out_{h1}{\partial net_{h1}} = out_{h1}(1 - out_{h1}) = 0.59326999(1 - 0.59326999 ) = 0.241300709$

Nous calculons la dérivée partielle de l’entrée totale du réseau à $h_1$ par rapport à $w_1$ de la même manière que nous l’avons fait pour le neurone de sortie :

$net_{h1} = w_1 * i_1 + w_3 * i_2 + b_1 * 1$

$\frac{\partial net_{h1}{\partial w_1} = i_1 = 0.05$

Mise en relation:

$\frac{\partial E_{total}{\partial w_{1}} = \frac{\partial E_{total}{\partial out_{h1}} * \frac{\partial out_{h1}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial w_{1}} = 0,036350306 * 0,241300709 * 0,05 = 0.000438568$

Vous pourriez aussi voir cela écrit comme:

$\frac{\partial E_{total}}{\partial w_{1}} = (\sum\limits_{o}{\frac{\partial E_{total}}{\partial out_{o}} * \frac{\partial out_{o}}{\partial net_{o}} * \frac{\partial net_{o}}{\partial out_{h1}}) * \frac{\partial out_{h1}}{\partial net_{h1}} * \frac{\partial net_{h1}}{\partial w_{1}}$

$\frac{\partial E_{total}}{\partial w_{1}} = (\sum\limits_{o}{\delta_{o} * w_{ho}}) * out_{h1}(1 - out_{h1}) * i_{1}$

$\frac{\partial E_{total}{\partial w_{1}} = \delta_{h1}i_{1}$

Nous pouvons maintenant mettre à jour $w_1$ :

$w_1^{+} = w_1 - \eta * \frac{\partial E_{total}}{\partial w_{1}} = 0.15 - 0.5 * 0.000438568 = 0.149780716$

Répéter cela pour $w_2$ $w_3$ , et $w_4$

$w_2^{+} = 0.19956143$

$w_3^{+} = 0,24975114$

$w_4^{+} = 0,29950229$

Enfin, nous avons mis à jour tous nos poids ! Lorsque nous avons fait avancer les entrées 0,05 et 0,1 à l’origine, l’erreur du réseau était de 0,298371109. Après ce premier tour de rétropropagation, l’erreur totale est maintenant réduite à 0,291027924. Cela peut sembler peu, mais après avoir répété ce processus 10 000 fois, par exemple, l’erreur tombe à 0,0000351085. À ce stade, lorsque nous alimentons 0,05 et 0,1, les deux neurones de sortie génèrent 0,015912196 (vs 0,01 cible) et 0,984065734 (vs 0,99 cible).

Si vous êtes arrivé jusqu’ici et que vous avez trouvé des erreurs dans l’un des éléments ci-dessus ou si vous pensez à des moyens de rendre les choses plus claires pour les futurs lecteurs, n’hésitez pas à me laisser un mot. Merci!

Contexte

Backpropagation en Python

Visualisation de la rétropropagation

Ressources supplémentaires

Overview

Le passage en avant

Calcul de l’erreur totale

La rétropropagation

Couche de sortie

Couche cachée

Laisser un commentaire Annuler la réponse