C’est un vecteur:

Un vecteur a une magnitude (taille) et une direction :
La longueur de la ligne indique sa magnitude et la pointe de la flèche indique la direction.
On peut ajouter deux vecteurs en les joignant tête-bêche :
Et peu importe l’ordre dans lequel on les ajoute, on obtient le même résultat :
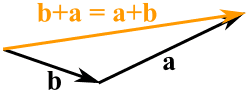
Exemple : Un avion vole, en pointant vers le Nord, mais il y a un vent qui vient du Nord-Ouest.
Les deux vecteurs (la vitesse provoquée par l’hélice, et la vitesse du vent) se traduisent par une vitesse au sol légèrement plus lente en se dirigeant un peu à l’Est du Nord.
Si vous observiez l’avion depuis le sol, il semblerait qu’il glisse un peu sur le côté.
Avez-vous déjà vu cela se produire ? Peut-être avez-vous vu des oiseaux luttant contre un vent fort qui semblent voler de côté. Les vecteurs aident à expliquer cela.
La vitesse, l’accélération, la force et bien d’autres choses sont des vecteurs.
Soustraire
On peut aussi soustraire un vecteur d’un autre :
- d’abord on inverse la direction du vecteur qu’on veut soustraire,
- puis on les additionne comme d’habitude :
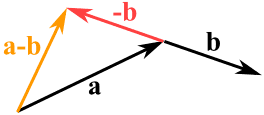
a – b
Notation
Un vecteur est souvent écrit en gras, comme a ou b.
| Un vecteur peut également être écrit comme les lettres de sa tête et de sa queue avec une flèche au-dessus, comme ceci : |
 |
Calculs
Maintenant …. comment faisons-nous les calculs ?
La façon la plus courante est de commencer par décomposer les vecteurs en parties x et y, comme ceci :
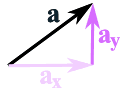
Le vecteur a est décomposé en
les deux vecteurs ax et ay
(Nous verrons plus tard comment faire.)
Ajout de vecteurs
On peut alors additionner des vecteurs en additionnant les parties x et en additionnant les parties y :
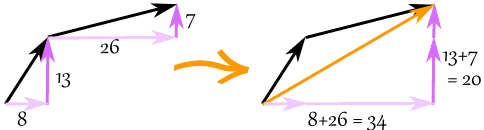
Le vecteur (8, 13) et le vecteur (26, 7) s’additionnent pour donner le vecteur (34, 20)
Exemple : additionner les vecteurs a = (8, 13) et b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Lorsqu’on décompose un vecteur comme cela, chaque partie est appelée composante :
Soustraction de vecteurs
Pour soustraire, il faut d’abord inverser le vecteur que l’on veut soustraire, puis ajouter.
Exemple : soustraire k = (4, 5) de v = (12, 2)
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
Magnitude d’un vecteur
La magnitude d’un vecteur est représentée par deux barres verticales de part et d’autre du vecteur :
|a|
OU elle peut être écrite avec des barres verticales doubles (pour ne pas la confondre avec la valeur absolue) :
||a|
On utilise le théorème de Pythagore pour le calculer :
|a| = √( x2 + y2 )
Exemple : quelle est la grandeur du vecteur b = (6, 8) ?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Un vecteur de magnitude 1 est appelé vecteur unitaire.
Vecteur vs scalaire
Un scalaire a une magnitude (taille) uniquement.
Scalaire : juste un nombre (comme 7 ou -0,32) .. définitivement pas un vecteur.
Un vecteur a une magnitude et une direction, et est souvent écrit en gras, donc on sait que ce n’est pas un scalaire:
- donc c est un vecteur, il a une magnitude et une direction
- mais c est juste une valeur, comme 3 ou 12.4
Exemple : kb est en fait le scalaire k multiplié par le vecteur b.
Multiplication d’un vecteur par un scalaire
Lorsque nous multiplions un vecteur par un scalaire, cela s’appelle « mettre à l’échelle » un vecteur, car nous changeons la taille du vecteur.
Exemple : multiplier le vecteur m = (7, 3) par le scalaire 3
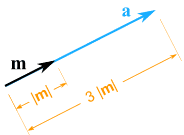 |
a = 3m = (3×7, 3×3) = (21, 9) |
Il pointe toujours dans la même direction, mais il est 3 fois plus long
(Et maintenant vous savez pourquoi les nombres sont appelés « scalaires », car ils « mettent à l’échelle » le vecteur vers le haut ou vers le bas.)
Multiplier un vecteur par un vecteur (produit scalaire et produit en croix)
 |
Comment multiplie-t-on deux vecteurs ensemble ? Il y a plus d’une façon !
(Lisez ces pages pour plus de détails.) |
Plus de 2 dimensions
Les vecteurs fonctionnent aussi parfaitement en 3 dimensions ou plus :
Le vecteur (1, 4, 5)
Exemple : additionner les vecteurs a = (3, 7, 4) et b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Exemple : quelle est la grandeur du vecteur w = (1, -2, 3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9) = √14
Voici un exemple à 4 dimensions (mais c’est difficile à dessiner !).):
Exemple : soustraire (1, 2, 3, 4) de (3, 3, 3, 3)
(3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3) + (-1,-2,-3,-4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Magnitude et direction
On peut connaître la magnitude et la direction d’un vecteur, mais vouloir ses longueurs x et y (ou vice versa) :
 |
<> |  |
| Vecteur a en coordonnées polaires Coordinates |
Vecteur a en coordonnées cartésiennes Coordinates . a en coordonnées cartésiennes Coordinates |
Vous pouvez lire comment les convertir à Coordonnées polaires et cartésiennes, mais voici un résumé rapide :
| Des coordonnées polaires (r,θ) aux coordonnées cartésiennes (x,y) |
Des coordonnées cartésiennes (x,y) aux coordonnées polaires (r,θ) |
|
|
|---|
Un exemple
Sam et Alex tirent une boîte.
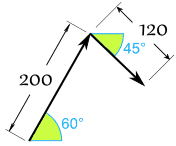
- Sam tire avec une force de 200 Newtons à 60°
- Alex tire avec une force de 120 Newtons à 45° comme indiqué
Quelle est la force combinée, et sa direction ?
Ajoutons les deux vecteurs tête-bêche :
D’abord, convertissons de polaire à cartésien (à 2 décimales):
Le vecteur de Sam:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0,8660 = 173.21
Vecteur d’Alex:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0,7071 = 84,85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84,85
Nous avons maintenant :
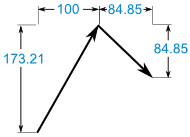
Ajoutez-les :
(100, 173,21) + (84,85, -84,85) = (184.85, 88,36)
Cette réponse est valide, mais reconvertissons en polaire puisque la question était en polaire :
- r = √ ( x2 + y2 ) = √ ( 184,852 + 88,362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88.36 / 184.85 ) = 25.5°
Et nous avons ce résultat (arrondi):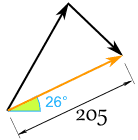
Et cela ressemble à ceci pour Sam et Alex:
Ils pourraient obtenir un meilleur résultat s’ils étaient épaule contre épaule!
.





