Implementação do Algoritmo Diffie-Hellman

Background

Criptografia de Curvas Elípticas (ECC) é uma abordagem à criptografia de chaves públicas, baseada na estrutura algébrica das curvas elípticas sobre campos finitos. A ECC requer uma chave mais pequena em comparação com a criptografia não-ECC para proporcionar uma segurança equivalente (uma segurança ECC de 256 bits tem uma segurança equivalente alcançada pela criptografia RSA de 3072 bits).
Para uma melhor compreensão da Criptografia de Curva Elíptica, é muito importante compreender os princípios básicos da Curva Elíptica. Uma curva elíptica é uma curva algébrica planar definida por uma equação da forma

Onde ‘a’ é o coeficiente de x e ‘b’ é a constante da equação

br>>p>p> A curva é não-singular; ou seja, o seu gráfico não tem cúspides ou auto-intersecções (quando a característica do campo Co-eficiente é igual a 2 ou 3).
Em geral, uma curva elíptica tem o aspecto mostrado abaixo. As curvas elípticas podem intersectar quase 3 pontos quando uma linha recta é traçada intersectando a curva. Como podemos ver, a curva elíptica é simétrica em relação ao eixo x, esta propriedade desempenha um papel chave no algoritmo.

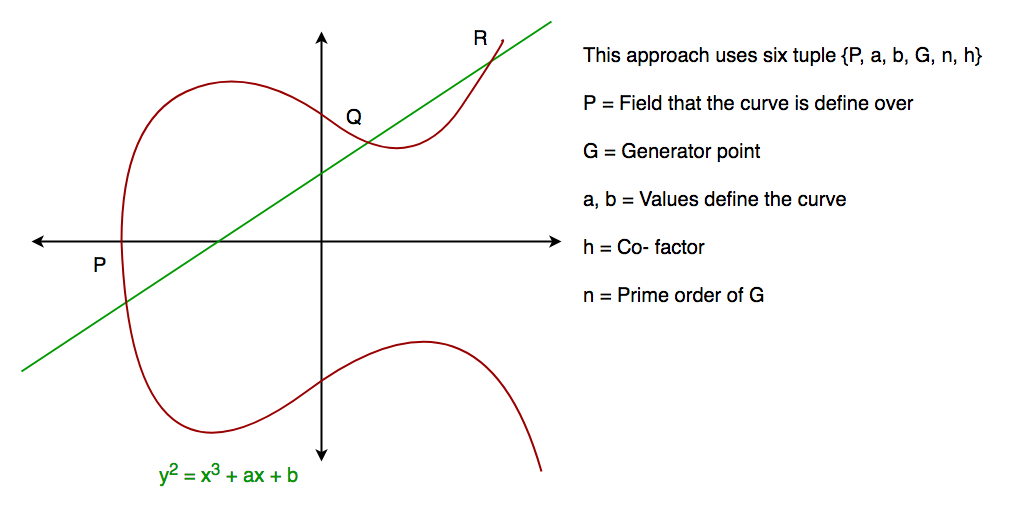
Curva Elíptica

algoritmo Diffie-Hellman

O algoritmo Diffie-Hellman está a ser usado para estabelecer um segredo partilhado que pode ser usado para comunicações secretas enquanto se trocam dados através de uma rede pública usando a curva elíptica para gerar pontos e obter a chave secreta usando os parâmetros.

Por uma questão de simplicidade e implementação prática do algoritmo, consideraremos apenas 4 variáveis um P e G (uma raiz primitiva de P) e dois valores privados a e b.
P e G são ambos números publicamente disponíveis. Os utilizadores (digamos Alice e Bob) escolhem valores privados a e b e geram uma chave e trocam-na publicamente, a pessoa oposta recebeu a chave e a partir daí gera uma chave secreta após a qual têm a mesma chave secreta para encriptar.

P>Passo por Passo Explicação

Alice	Bob
Public Keys available = P, G	Public Keys available = P, G
Chave Privada Seleccionada = a	Chave Privada Seleccionada = b
Key generated =	Key generated = >p>
key received = x
Generated Secret Key =	Chave Secreta Gerada = k_b = x^b mod P
“>p>Algebraicamente pode ser mostrado que

Exemplo

Step 1: Alice and Bob get public numbers P = 23, G = 9Step 2: Alice selected a private key a = 4 and Bob selected a private key b = 3Step 3: Alice and Bob compute public valuesAlice: x =(9^4 mod 23) = (6561 mod 23) = 6 Bob: y = (9^3 mod 23) = (729 mod 23) = 16Step 4: Alice and Bob exchange public numbersStep 5: Alice receives public key y =16 and Bob receives public key x = 6Step 6: Alice and Bob compute symmetric keys Alice: ka = y^a mod p = 65536 mod 23 = 9 Bob: kb = x^b mod p = 216 mod 23 = 9Step 7: 9 is the shared secret.

Implantação:

div>>div>

>/p>

div>>>br>

#include<stdio.h>

#include<math.h>

longlongintpower(longlonginta, longlongintb,

longlongintP)

{

if(b == 1)

returna;

else

return(((longlongint)pow(a, b)) % P);

}

intmain()

{

longlongintP, G, x, a, y, b, ka, kb;

P = 23;

printf("The value of P : %lld\n", P);

G = 9;

printf("The value of G : %lld\n\n", G);

a = 4;

printf("The private key a for Alice : %lld\n", a);

x = power(G, a, P);

b = 3;

printf("The private key b for Bob : %lld\n\n", b);

y = power(G, b, P);

ka = power(y, a, P);

kb = power(x, b, P);

printf("Secret key for the Alice is : %lld\n", ka);

printf("Secret Key for the Bob is : %lld\n", kb);

return0;

}

Python3

>/p>

fromrandom importrandint

if__name__ =='__main__':

P =23

G =9

print('The Value of P is :%d'%(P))

print('The Value of G is :%d'%(G))

a =4

print('The Private Key a for Alice is :%d'%(a))

x =int(pow(G,a,P))

b =3

print('The Private Key b for Bob is :%d'%(b))

y =int(pow(G,b,P))

ka =int(pow(y,a,P))

kb =int(pow(x,b,P))

print('Secret key for the Alice is : %d'

%(ka))

print('Secret Key for the Bob is : %d'%(kb))

Saída

The value of P : 23The value of G : 9The private key a for Alice : 4The private key b for Bob : 3Secret key for the Alice is : 9Secret Key for the Bob is : 9

Este artigo é contribuído por Souvik Nandi. Se gosta de GeeksforGeeks e gostaria de contribuir, pode também escrever um artigo usando o contribute.GeeksforGeeks.org ou enviar o seu artigo por correio para [email protected]. Veja o seu artigo que aparece na página principal de GeeksforGeeks e ajude outros Geeks.
Por favor escreva comentários se encontrar algo incorrecto, ou se quiser partilhar mais informação sobre o tópico discutido acima.

Etiquetas de artigos :

Etiqueta de prática :

Deixe uma resposta Cancelar resposta