Nel mondo reale, le oscillazioni raramente seguono il vero SHM. L’attrito di qualche tipo di solito agisce per smorzare il moto in modo che muoia, o ha bisogno di più forza per continuare. In questa sezione, esaminiamo alcuni esempi di moto armonico smorzato e vediamo come modificare le equazioni del moto per descrivere questo caso più generale.

Una corda di chitarra smette di oscillare pochi secondi dopo essere stata pizzicata. Per continuare a dondolare sull’altalena di un parco giochi, devi continuare a spingere (Figura \PageIndex{1}}). Anche se spesso possiamo rendere l’attrito e altre forze non conservative piccole o trascurabili, il moto completamente non smorzato è raro. Infatti, potremmo anche voler smorzare le oscillazioni, come nel caso degli ammortizzatori delle automobili.

La figura \(\PageIndex{2}}) mostra una massa m attaccata ad una molla con una costante di forza k. La massa viene sollevata ad una posizione A0, l’ampiezza iniziale, e poi rilasciata. La massa oscilla intorno alla posizione di equilibrio in un fluido con viscosità, ma l’ampiezza diminuisce per ogni oscillazione. Per un sistema che ha una piccola quantità di smorzamento, il periodo e la frequenza sono costanti e sono quasi gli stessi di SHM, ma l’ampiezza diminuisce gradualmente come mostrato. Questo accade perché la forza di smorzamento non conservativa rimuove energia dal sistema, di solito sotto forma di energia termica.

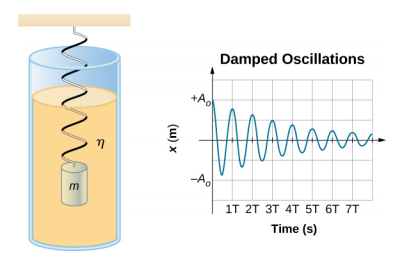
Considera le forze che agiscono sulla massa. Si noti che l’unico contributo del peso è quello di cambiare la posizione di equilibrio, come discusso in precedenza nel capitolo. Pertanto, la forza netta è uguale alla forza della molla e alla forza di smorzamento (\(F_D\)). Se la grandezza della velocità è piccola, cioè la massa oscilla lentamente, la forza di smorzamento è proporzionale alla velocità e agisce contro la direzione del moto (\(F_D = -b\)). La forza netta sulla massa è quindi

Scrivendo questo come un’equazione differenziale in x, otteniamo

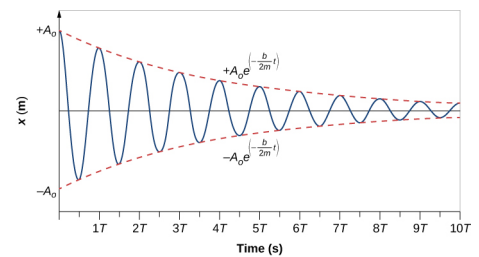
Per determinare la soluzione di questa equazione, consideriamo il grafico della posizione contro il tempo mostrato nella figura \(\PageIndex{3}). La curva assomiglia ad una curva di coseno che oscilla nell’inviluppo di una funzione esponenziale \(A_0e^{-alpha t}\) dove \(\alpha = \fracb}{2m}\). La soluzione è

Si lascia come esercizio dimostrare che questa è, infatti, la soluzione. Per dimostrare che è la soluzione giusta, si prendono le derivate prima e seconda rispetto al tempo e si sostituiscono all’equazione 15.23. Si trova che l’equazione 15.24 è la soluzione se

\

Ricordiamo che la frequenza angolare di una massa sottoposta a SHM è uguale alla radice quadrata della costante di forza divisa per la massa. Questo è spesso indicato come la frequenza angolare naturale, che è rappresentata come

\

La frequenza angolare per il moto armonico smorzato diventa

\

Ricordiamo che quando abbiamo iniziato questa descrizione del moto armonico smorzato, abbiamo affermato che lo smorzamento deve essere piccolo. Vengono in mente due domande. Perché lo smorzamento deve essere piccolo? E quanto piccolo è piccolo? Se si aumenta gradualmente la quantità di smorzamento in un sistema, il periodo e la frequenza cominciano ad essere influenzati, perché lo smorzamento si oppone e quindi rallenta il movimento avanti e indietro. (La forza netta è più piccola in entrambe le direzioni). Se lo smorzamento è molto grande, il sistema non oscilla nemmeno – si muove lentamente verso l’equilibrio. La frequenza angolare è uguale a

Come b aumenta, \(\frac{k}{m} – \left(\dfrac{b}{2m}}right)^{2}}) diventa più piccola e alla fine raggiunge lo zero quando b = \(\sqrt{4mk}\). Se b diventa più grande, \frac{k}{m} – \sinistra(\dfrac{b}{2m}destra)^{2}}) diventa un numero negativo e \sqrt{frac{k}{m} – \sinistra(\dfrac{b}{2m}destra)^{2}}) è un numero complesso.

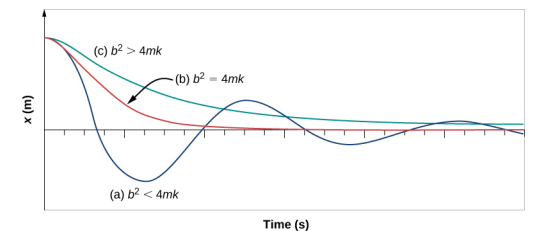
La figura \(\PageIndex{4}) mostra lo spostamento di un oscillatore armonico per diverse quantità di smorzamento.

1. Quando la costante di smorzamento è piccola, b < \(\sqrt{4mk}\), il sistema oscilla mentre l’ampiezza del moto decade esponenzialmente. Questo sistema si dice che è sottosmorzato, come nella curva (a). Molti sistemi sono sottosmorzati, e oscillano mentre l’ampiezza diminuisce esponenzialmente, come la massa che oscilla su una molla. Lo smorzamento può essere abbastanza piccolo, ma alla fine la massa si ferma.
2. Se la costante di smorzamento è \(b = \sqrt{4mk}\), il sistema è detto essere smorzato criticamente, come nella curva (\(b\)). Un esempio di un sistema criticamente smorzato sono gli ammortizzatori di un’automobile. È vantaggioso che le oscillazioni decadano il più velocemente possibile. Qui, il sistema non oscilla, ma si avvicina asintoticamente alla condizione di equilibrio il più velocemente possibile.
3. La curva (c) nella figura \(\PageIndex{4}}) rappresenta un sistema sovrasmorzato dove \(b > \sqrt{4mk}\). Un sistema sovrasmorzato si avvicinerà all’equilibrio in un periodo di tempo più lungo.

Lo smorzamento critico è spesso desiderato, perché un tale sistema ritorna all’equilibrio rapidamente e rimane anche all’equilibrio. Inoltre, una forza costante applicata ad un sistema criticamente smorzato muove il sistema verso una nuova posizione di equilibrio nel più breve tempo possibile, senza overshooting o oscillazioni sulla nuova posizione.