Introduzione

Column buckling è un argomento curioso e unico. È forse l’unica area della meccanica strutturale in cui il cedimento non è legato alla resistenza del materiale. Un’analisi dell’instabilità delle colonne consiste nel determinare il carico massimo che una colonna può sopportare prima di collassare. Ma per le colonne lunghe, il collasso non ha nulla a che fare con lo snervamento del materiale. È invece governato dalla rigidità della colonna, sia materiale che geometrica.
Questa pagina deriverà le equazioni standard dell’instabilità della colonna usando due approcci. Questa è la derivazione che si trova nei libri di testo e presentata nei corsi di ingegneria. Ma non mi è mai piaciuta. Non perché sia errata (è corretta), ma perché non penso che presenti in modo soddisfacente i meccanismi fisici che governano il processo di instabilità. Ecco perché sarà presentata anche una seconda derivazione delle equazioni di instabilità.
Curiosamente, gli oggetti sono indicati come colonne quando sono caricati assialmente in compressione, come è il caso qui, ma sono indicati come travi quando sono caricati trasversalmente.
Nonostante, la teoria della flessione della trave è centrale per le analisi di instabilità della colonna, quindi si raccomanda al lettore di rivedere questa pagina sulla flessione della trave.

Teoria dell’instabilità di Eulero

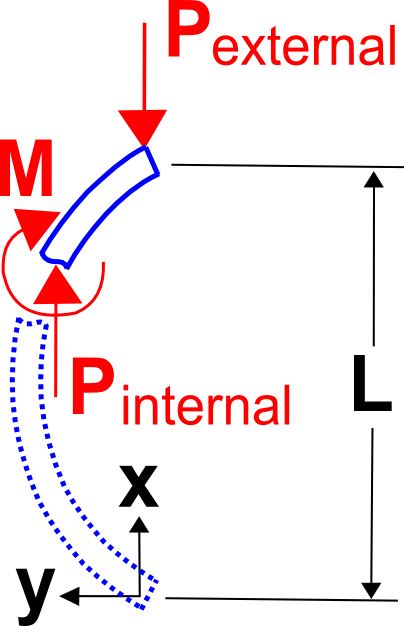
La teoria dell’instabilità di Eulero è la teoria classica presentata nei libri di testo e in classe. Inizia semplicemente notando che il momento flettente interno in una colonna caricata e deformata è \(-P \, y\) dove \(P \) è il carico di compressione e \(y\) è la flessione della colonna. Quindi inserire \(-P \, y\) per \(M\) nell’equazione di flessione della trave, \( E \, I \, y” = M \).

Questo produce la seguente equazione differenziale
che ha la soluzione

dove \(A\) e \(B\) sono costanti determinate dalle condizioni al contorno.
Le condizioni al contorno sono \(y = 0\) a \(x = 0\) e \(x = L\).
La prima condizione al contorno, \(y = 0\) a \(x = 0\), porta alla conclusione che \(B = 0\). E questo lascia

Fin qui tutto bene. Ma è a questo punto che la derivazione classica tende ad abbandonare l’intuizione fisica per diventare apertamente matematica…
Le cose diventano molto interessanti con la seconda condizione al contorno perché, come vedremo, non porta alla determinazione della costante sconosciuta, \(A\). Per vedere questo, inseriamo la seconda condizione al contorno come segue.

Ci sono fondamentalmente due possibilità qui. Nel primo caso, \(A = 0\), ma questo è noioso perché porta al risultato che tutti gli spostamenti sono zero. Questa è solo la soluzione senza fibbia. Prima che la colonna si inverta, i suoi spostamenti laterali sono semplicemente zero.

Il secondo caso è quello interessante, e quello direttamente collegato all’inveramento della colonna. Il secondo metodo per soddisfare la condizione limite è notare che \(\sin(\pi) = 0\). Quindi il modo di soddisfare la condizione al contorno è di richiedere che l’argomento dell’equazione, \(\sinistra( \sqrt{P \su E \, I}}; L \destra)\ deve essere uguale a \(\pi\).Facendo così si ottiene

\br>e risolvendo per \(P\) si ottiene

Questo è il classico risultato della teoria dell’instabilità di Eulero. Dà il valore critico del carico \(P\), chiamato \(P_{cr}\), oltre il quale, la colonna si deformerà. uesto risultato è perfettamente legittimo. Tuttavia, come dovrebbe essere evidente ormai, è molto matematico in natura, e fornisce poca comprensione fisica come risultato. La derivazione che segue presenterà un metodo alternativo per arrivare alla stessa equazione che credo fornisca una connessione fisica molto più diretta al processo di deformazione rispetto alla derivazione precedente.

Buckling vs Yielding

Come detto all’inizio, l’analisi classica di buckling è indipendente dal carico di snervamento di un materiale. Questo è evidente nella derivazione di cui sopra, perché in nessun momento lo stress o la deformazione sono stati discussi o confrontati con la resistenza di un materiale. a in effetti, le considerazioni sullo snervamento non dovrebbero mai essere totalmente ignorate. Una volta ottenuta una stima di (P_cr) dall’equazione di cui sopra, si dovrebbe sempre dividerla per l’area della sezione trasversale della colonna, (A), per ottenere una sollecitazione e confrontare questo valore con il limite di snervamento del materiale per determinare se lo snervamento avverrà prima della deformazione. Questo è critico per le colonne corte perché hanno intrinsecamente alti valori di \(P_cr}\ perché \(L^2\) è nel denominatore della equazione di instabilità.

Costrizioni finali nell’imbarcamento

Anche se non è l’obiettivo di questa pagina, è importante riconoscere che i vincoli di estremità sono critici per le analisi di instabilità perché alterano il valore di \(P_cr}\). Per esempio, si consideri che il carico critico di instabilità della colonna mostrata qui è dato da

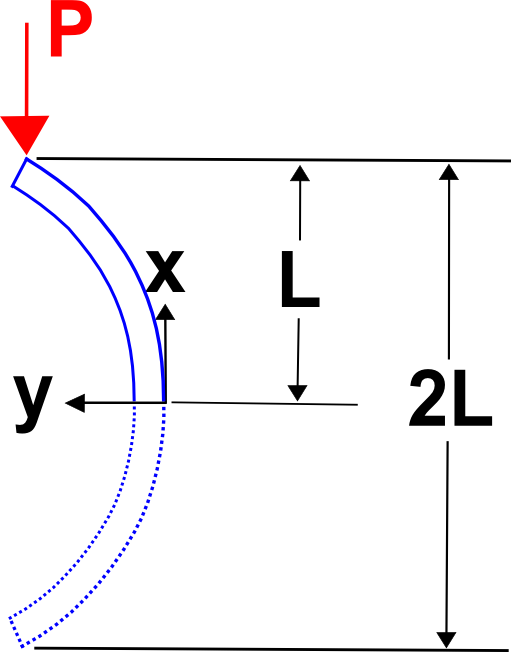
Nota che questo valore è 1/4 di quello dato nell’equazione precedente per \(P_cr}\).Ma è facile capire perché. Lo schizzo mostra che la condizione di instabilità qui è esattamente equivalente all’instabilità di una colonna di lunghezza doppia e con le stesse condizioni al contorno della derivazione precedente. E questo porta a

Derivazione dell’instabilità basata sulla fisica

Questa sezione presenterà un metodo alternativo per determinare i carichi critici di instabilità che credo sia più fisicamente intuitivo della classica teoria di Eulero dell’instabilità. La sua caratteristica chiave è il confronto del momento flettente interno derivante dalla distribuzione interna delle sollecitazioni con il momento flettente esterno risultante dal carico applicato alla colonna. (La frase precedente è critica.)
Questo approccio riprende approssimativamente dove è stato notato prima che l’approccio classico di Eulero diventa apertamente matematico. Il primo passo è assumere una forma deformata. Sappiamo che \(y = 0\) alle due estremità della colonna, e che la forma segue una funzione \(\sin()\) basata sull’equazione abovedifferenziale. Quindi la scelta più logica è

dove \(\delta_{max}\ è lo spostamento laterale al punto medio della colonna. Il suo valore è sconosciuto, ma si sa che è maggiore nel punto medio che in qualsiasi altro punto della colonna, da qui il pedice \(max). La scelta di \(\pi x / L\) come argomento della funzione \(\sin()\) assicura che gli spostamenti siano zero in \(x = 0\) e \(x = L\). (Parleremo di altre forme assunte a breve.)

Se vi state chiedendo del termine \(\sqrt{P/EI}) nella funzione \(\sin()\) della precedente soluzione di Eulero, non fatelo. Esso deriva dalla soluzione dell’equazione differenziale, ma qui facciamo finta di non sapere nulla dei dettagli di quella soluzione (attenzione all’eccezione!). Abbiamo solo bisogno di una funzione che possa assomigliare a una colonna piegata con spostamenti nulli alle sue estremità. Usando \(\sin ( {\pi x \su L} )\ si ottiene questo.
L'”allarme eccezione” è presente qui sopra perché in effetti stiamo sfruttando un pezzo di conoscenza dell’analisi precedente. E’ che le funzioni trigonometriche sono le soluzioni dell’equazione differenziale, quindi, i seni e i coseni dovrebbero essere usati quando possibile per descrivere le forme deformate, perché porteranno alle stime più accurate di \(P_{cr}\.

Ricordiamo dalla teoria della flessione delle travi che il momento flettente, \(M\), è legato alla deflessione della colonna da

Anche se non è critico, è utile ricordare che questa relazione è venuta dal calcolo del momento nella sezione trasversale dovuto alla distribuzione delle sollecitazioni. La relazione mostra che abbiamo bisogno della derivata seconda della funzione di spostamento ipotizzata.

\
Questo è il momento flettente interno della colonna dovuto alla distribuzione delle sollecitazioni al suo interno, che è a sua volta dovuto al fatto che la colonna è piegata.
Ecco un pensiero importante… Questo momento flettente può essere pensato come la resistenza interna della colonna alla flessione, o la forza con cui cerca di raddrizzarsi.
Il semplice passo successivo è quello di equiparare questo momento flettente interno resistivo a quello risultante dal carico esterno. Questa quantità è semplicemente (M = -P \, y(x)\). Eguagliando i due dà

Non è difficile vedere a questo punto che questo approccio sta portando alla stessa espressione per \(P_{cr}\) come la classica teoria dell’instabilità di Eulero ha fatto.ma lungo la strada, ha fornito molto più comprensione nel processo fisico di instabilità che la teoria precedente. Vale a dire…

1. Siamo arrivati a questa relazione equiparando il momento flettente interno (dovuto alle sollecitazioni interne derivanti dalla flessione della colonna) al momento flettente esterno risultante dal carico esterno, \(P\).Dovrebbe essere chiaro che l’instabilità avviene quando \(P\) è abbastanza grande da soddisfare l’equazione. Qualsiasi valore inferiore, e \(P \, y(x)\) sarà inferiore al “momento flettente resistente.”
2. Il fatto che \(y(x)\) appare su entrambi i lati dell’equazione, e sarà quindi annullato, significa che quando l’instabilità avviene, lo fa simultaneamente per tutta la lunghezza della colonna. (Un risultato affascinante che non è evidente nella teoria di Eulero.)

Ad ogni modo, cancellando \(y(x)\) da entrambi i lati dell’equazione si ottiene

di nuovo, ma questa volta con molta più comprensione fisica.

Esempio di estremità fissa

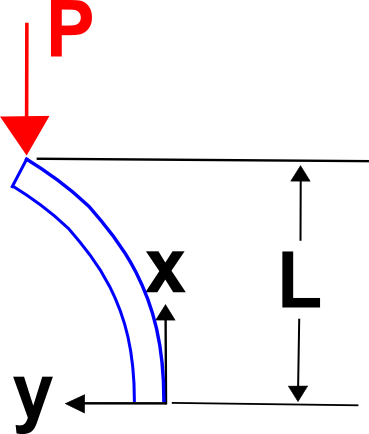
Questa volta, assumiamo una forma deformata di

Calcolare il momento flettente dovuto a questo.

Il momento flettente dovuto al carico esterno è \(M = P ( \delta_{max} – y(x) )\). Eguagliando questi due e semplificando si ottiene il noto risultato.

Esempio di estremità fissa con diversa forma ipotizzata

Questo esempio dimostrerà che si possono assumere funzioni alternative per la forma deformata della colonna, e che la formula risultante per \(P_{cr}\) non sarà significativamente diversa dalla soluzione esatta.
Questa volta, assumere una forma deformata di

Calcolare il momento flettente dovuto a questo.

Il momento flettente dovuto al carico esterno rimane \(M = P ( \delta_{max}) – y(x) )\). Eguagliando questi due si ottiene

E’ chiaro dall’equazione che il valore minimo di \(P) avverrà a \(x = 0\)perché è in questo punto che \(y(x)\ è un minimo (zero, infatti) e quindi \(\delta_{max} – y(x))\) è un massimo. Impostando \(y(x)\) a zero e cancellando \delta_{max} da entrambe le parti si ottiene

Questo risultato non è ovviamente uguale alla soluzione esatta di cui sopra. La differenza è che la soluzione esatta contiene \pi^2 / 4 = 2,467\), mentre questa soluzione approssimativa contiene 2, una differenza del 23%. Significativo, ma non grande come, diciamo, un fattore di 2, o un ordine di grandezza. Si noti inoltre che la soluzione approssimata è conservativa in quanto dà un carico critico di instabilità inferiore a quello della soluzione esatta.
È interessante notare che questa soluzione basata sulla forma quadratica, ha portato a un carico critico di instabilità inferiore e una concentrazione del cedimento di instabilità alla base della colonna, \(x = 0\).Al contrario, la soluzione esatta costituita dalla funzione trigonometrica, ha prodotto una tendenza all’instabilità uguale per tutta la lunghezza della colonna, e un corrispondente maggiore \(P_{cr}\).
Un fattore chiave qui è che la forma deformata quadratica assunta non è una soluzione esatta dell’equazione differenziale che governa (anche se è vicina). Le funzioni trigonometriche lo sono.