Ultimo aggiornamento del 25 settembre 2019

Invece di prevedere direttamente i valori delle classi per un problema di classificazione, può essere conveniente prevedere la probabilità che un’osservazione appartenga a ogni possibile classe.

Prevedere le probabilità permette una certa flessibilità, tra cui decidere come interpretare le probabilità, presentare le previsioni con incertezza e fornire modi più sfumati per valutare l’abilità del modello.

Le probabilità previste che corrispondono alla distribuzione attesa delle probabilità per ogni classe sono definite calibrate. Il problema è che non tutti i modelli di apprendimento automatico sono in grado di prevedere probabilità calibrate.

Ci sono metodi sia per diagnosticare quanto siano calibrate le probabilità previste sia per calibrare meglio le probabilità previste con la distribuzione osservata di ogni classe. Spesso, questo può portare a previsioni di migliore qualità, a seconda di come viene valutata l’abilità del modello.

In questo tutorial, scoprirete l’importanza della calibrazione delle probabilità previste e come diagnosticare e migliorare la calibrazione dei modelli usati per la classificazione probabilistica.

Dopo aver completato questo tutorial, saprete:

• Gli algoritmi lineari di apprendimento automatico spesso predicono probabilità di classe non calibrate.
• I diagrammi di affidabilità possono essere usati per diagnosticare la calibrazione di un modello, e i metodi possono essere usati per calibrare meglio le previsioni di un problema.
• Come sviluppare diagrammi di affidabilità e calibrare modelli di classificazione in Python con scikit-learn.

Avvia il tuo progetto con il mio nuovo libro Probability for Machine Learning, che include tutorial passo-passo e i file del codice sorgente Python per tutti gli esempi.

Iniziamo.

Come e quando usare un modello di classificazione calibrato con scikit-learn
Foto di Nigel Howe, alcuni diritti riservati.

Panoramica del tutorial

Questo tutorial è diviso in quattro parti; esse sono:

1. Previsione delle probabilità
2. Calibrazione delle previsioni
3. Come calibrare le probabilità in Python
4. Esempio di lavoro sulla calibrazione delle probabilità SVM

Previsione delle probabilità

Un problema di classificazione richiede la previsione di un’etichetta per una data osservazione.

In alternativa alla predizione diretta dell’etichetta, un modello può predire la probabilità che un’osservazione appartenga ad ogni possibile etichetta di classe.

Questo fornisce una certa flessibilità sia nel modo in cui le previsioni sono interpretate e presentate (scelta della soglia e dell’incertezza della previsione) sia nel modo in cui il modello è valutato.

Anche se un modello può essere in grado di prevedere le probabilità, la distribuzione e il comportamento delle probabilità possono non corrispondere alla distribuzione attesa delle probabilità osservate nei dati di addestramento.

Questo è particolarmente comune con algoritmi complessi di apprendimento automatico non lineare che non fanno direttamente previsioni probabilistiche e usano invece approssimazioni.

La distribuzione delle probabilità può essere regolata per corrispondere meglio alla distribuzione attesa osservata nei dati. Questo aggiustamento è chiamato calibrazione, come la calibrazione del modello o la calibrazione della distribuzione delle probabilità di classe.

desideriamo che le probabilità di classe stimate riflettano la vera probabilità sottostante del campione. Cioè, la probabilità di classe prevista (o il valore simile alla probabilità) deve essere ben calibrata. Per essere ben calibrate, le probabilità devono effettivamente riflettere la vera probabilità dell’evento di interesse.

– Pagina 249, Applied Predictive Modeling, 2013.

Calibrazione delle previsioni

Ci sono due preoccupazioni nella calibrazione delle probabilità; sono la diagnosi della calibrazione delle probabilità previste e il processo di calibrazione stesso.

Diagrammi di affidabilità (curve di calibrazione)

Un diagramma di affidabilità è un grafico a linee della frequenza relativa di ciò che è stato osservato (asse y) rispetto alla frequenza della probabilità prevista (asse x).

I diagrammi di affidabilità sono aiuti comuni per illustrare le proprietà dei sistemi di previsione probabilistica. Consistono in un grafico della frequenza relativa osservata contro la probabilità prevista, fornendo un rapido confronto visivo quando si mettono a punto sistemi di previsione probabilistica, oltre a documentare le prestazioni del prodotto finale

– Increasing the Reliability of Reliability Diagrams, 2007.

Specificamente, le probabilità previste sono divise in un numero fisso di bucket lungo l’asse x. Il numero di eventi (class=1) sono poi contati per ogni buco (per esempio la frequenza relativa osservata). Infine, i conteggi vengono normalizzati. Questi grafici sono comunemente chiamati diagrammi di “affidabilità” nella letteratura sulle previsioni, anche se possono essere chiamati anche grafici o curve di “calibrazione” in quanto riassumono il grado di calibrazione delle probabilità di previsione.

Meglio calibrata o più affidabile è una previsione, più vicini appariranno i punti lungo la diagonale principale dal basso a sinistra all’alto a destra del grafico.

La posizione dei punti o della curva rispetto alla diagonale può aiutare ad interpretare le probabilità; per esempio:

• Sotto la diagonale: Il modello ha over-forecast; le probabilità sono troppo grandi.
• Sopra la diagonale: Il modello ha under-forecast; le probabilità sono troppo piccole.

Le probabilità, per definizione, sono continue, quindi ci aspettiamo una certa separazione dalla linea, spesso mostrata come una curva a forma di S che mostra tendenze pessimistiche di over-forecasting di probabilità basse e under-forecasting di probabilità alte.

I diagrammi di affidabilità forniscono una diagnostica per controllare se il valore della previsione Xi è affidabile. In parole povere, una previsione di probabilità è affidabile se l’evento accade effettivamente con una frequenza relativa osservata coerente con il valore della previsione.

– Increasing the Reliability of Reliability Diagrams, 2007.

Il diagramma di affidabilità può aiutare a capire la calibrazione relativa delle previsioni di diversi modelli predittivi.

Calibrazione della probabilità

Le previsioni fatte da un modello predittivo possono essere calibrate.

Le previsioni calibrate possono (o non possono) risultare in una migliore calibrazione su un diagramma di affidabilità.

Alcuni algoritmi sono adattati in modo tale che le loro probabilità previste siano già calibrate. Senza entrare nei dettagli del perché, la regressione logistica è uno di questi esempi.

Altri algoritmi non producono direttamente previsioni di probabilità, e invece una previsione di probabilità deve essere approssimata. Alcuni esempi includono le reti neurali, le macchine vettoriali di supporto e gli alberi decisionali.

Le probabilità previste da questi metodi saranno probabilmente non calibrate e possono beneficiare di essere modificate attraverso la calibrazione.

La calibrazione delle probabilità di previsione è un’operazione di ridimensionamento che viene applicata dopo che le previsioni sono state fatte da un modello predittivo.

Ci sono due approcci popolari per calibrare le probabilità; sono il Platt Scaling e la Regressione Isotonica.

Platt Scaling è più semplice ed è adatto ai diagrammi di affidabilità con la forma a S. La Regressione Isotonica è più complessa, richiede molti più dati (altrimenti potrebbe sovraraffinare), ma può supportare diagrammi di affidabilità con forme diverse (è nonparametrica).

Platt Scaling è più efficace quando la distorsione nelle probabilità previste è di forma sigmoidale. La regressione isotonica è un metodo di calibrazione più potente che può correggere qualsiasi distorsione monotonica. Sfortunatamente, questo potere extra ha un prezzo. Un’analisi della curva di apprendimento mostra che la Regressione Isotonica è più incline all’overfitting, e quindi si comporta peggio del Platt Scaling, quando i dati sono scarsi.

– Predicting Good Probabilities With Supervised Learning, 2005.

Nota, e questo è davvero importante: probabilità meglio calibrate possono o non possono portare a migliori previsioni basate sulla classe o sulla probabilità. Dipende davvero dalla metrica specifica usata per valutare le previsioni.

In effetti, alcuni risultati empirici suggeriscono che gli algoritmi che possono beneficiare maggiormente della calibrazione delle probabilità previste includono SVM, alberi decisionali insacchettati e foreste casuali.

dopo la calibrazione i metodi migliori sono gli alberi boostati, le foreste casuali e gli SVM.

– Predicting Good Probabilities With Supervised Learning, 2005.

Come calibrare le probabilità in Python

La libreria di apprendimento automatico scikit-learn permette sia di diagnosticare la calibrazione delle probabilità di un classificatore sia di calibrare un classificatore che può prevedere le probabilità.

Diagnosticare la calibrazione

È possibile diagnosticare la calibrazione di un classificatore creando un diagramma di affidabilità delle probabilità effettive rispetto alle probabilità previste su un set di test.

In scikit-learn, questo è chiamato curva di calibrazione.

Questo può essere implementato calcolando prima la funzione calibration_curve(). Questa funzione prende i valori delle classi vere per un set di dati e le probabilità previste per la classe principale (class=1). La funzione restituisce le probabilità vere per ogni bin e le probabilità previste per ogni bin. Il numero di bin può essere specificato tramite l’argomento n_bins e il default è 5.

Per esempio, qui sotto c’è uno snippet di codice che mostra l’uso dell’API:

Calibra il classificatore

Un classificatore può essere calibrato in scikit-learn usando la classe CalibratedClassifierCV.

Ci sono due modi per usare questa classe: prefit e cross-validation.

È possibile adattare un modello su un set di dati di allenamento e calibrare questo modello prefit usando un set di dati di convalida.

Per esempio, qui sotto c’è uno snippet di codice che mostra l’uso delle API:

1 2 3 4 5 6 7 8 9 10 11 12 13

… # preparare i dati trainX, trainy = … valX, valy = … testX, testy = … # adatta il modello di base sul set di dati di allenamento model = … model.fit(trainX, trainy) # calibra il modello sui dati di validazione calibratore = CalibratedClassifierCV(model, cv=’prefit’) calibratore.fit(valX, valy) # valuta il modello yhat = calibratore.predict(testX)

Alternativamente, il CalibratedClassifierCV può adattare più copie del modello usando k-fold cross-validation e calibrare le probabilità predette da questi modelli usando il set di hold out. Le previsioni sono fatte usando ciascuno dei modelli addestrati.

Per esempio, qui sotto c’è uno snippet di codice che mostra l’uso delle API:

1 2 3 4 5 6 7 8 9 10 11

… # preparare i dati trainX, trainy = … testX, testy = … # definire il modello di base model = … # adatta e calibra il modello sui dati di allenamento calibratore = CalibratedClassifierCV(modello, cv=3) calibratore.fit(trainX, trainy) # valuta il modello yhat = calibratore.predict(testX)

La classe CalibratedClassifierCV supporta due tipi di calibrazione delle probabilità; in particolare, il metodo parametrico ‘sigmoide’ (metodo di Platt) e il metodo non parametrico ‘isotonico’ che può essere specificato tramite l’argomento ‘method’.

Esempio di lavoro sulla calibrazione delle probabilità SVM

Possiamo concretizzare la discussione sulla calibrazione con alcuni esempi di lavoro.

In questi esempi, adatteremo una macchina a vettore di supporto (SVM) a un problema di classificazione binaria rumorosa e useremo il modello per prevedere le probabilità, poi rivedremo la calibrazione usando un diagramma di affidabilità e calibreremo il classificatore e rivedremo il risultato.

SVM è un buon modello candidato da calibrare perché non prevede nativamente le probabilità, il che significa che le probabilità sono spesso non calibrate.

Una nota su SVM: le probabilità possono essere previste chiamando la funzione decision_function() sul modello adatto invece della solita funzione predict_proba(). Le probabilità non sono normalizzate, ma possono essere normalizzate quando si chiama la funzione calibration_curve() impostando l’argomento ‘normalize’ a ‘True’.

L’esempio seguente adatta un modello SVM al problema di test, predice le probabilità e traccia la calibrazione delle probabilità come diagramma di affidabilità,

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

# Diagramma di affidabilità SVM da sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # dividere in set train/test trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # adatta un modello model = SVC() model.fit(trainX, trainy) # prevedere le probabilità probs = model.decision_function(testX) # diagramma di affidabilità fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot perfettamente calibrato pyplot.plot(, , linestyle=’–‘) # traccia l’affidabilità del modello pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

L’esecuzione dell’esempio crea un diagramma di affidabilità che mostra la calibrazione delle probabilità previste da SVM (linea continua) rispetto a un modello perfettamente calibrato lungo la diagonale del grafico (linea tratteggiata.)

Possiamo vedere la curva prevista a forma di S di una previsione conservativa.

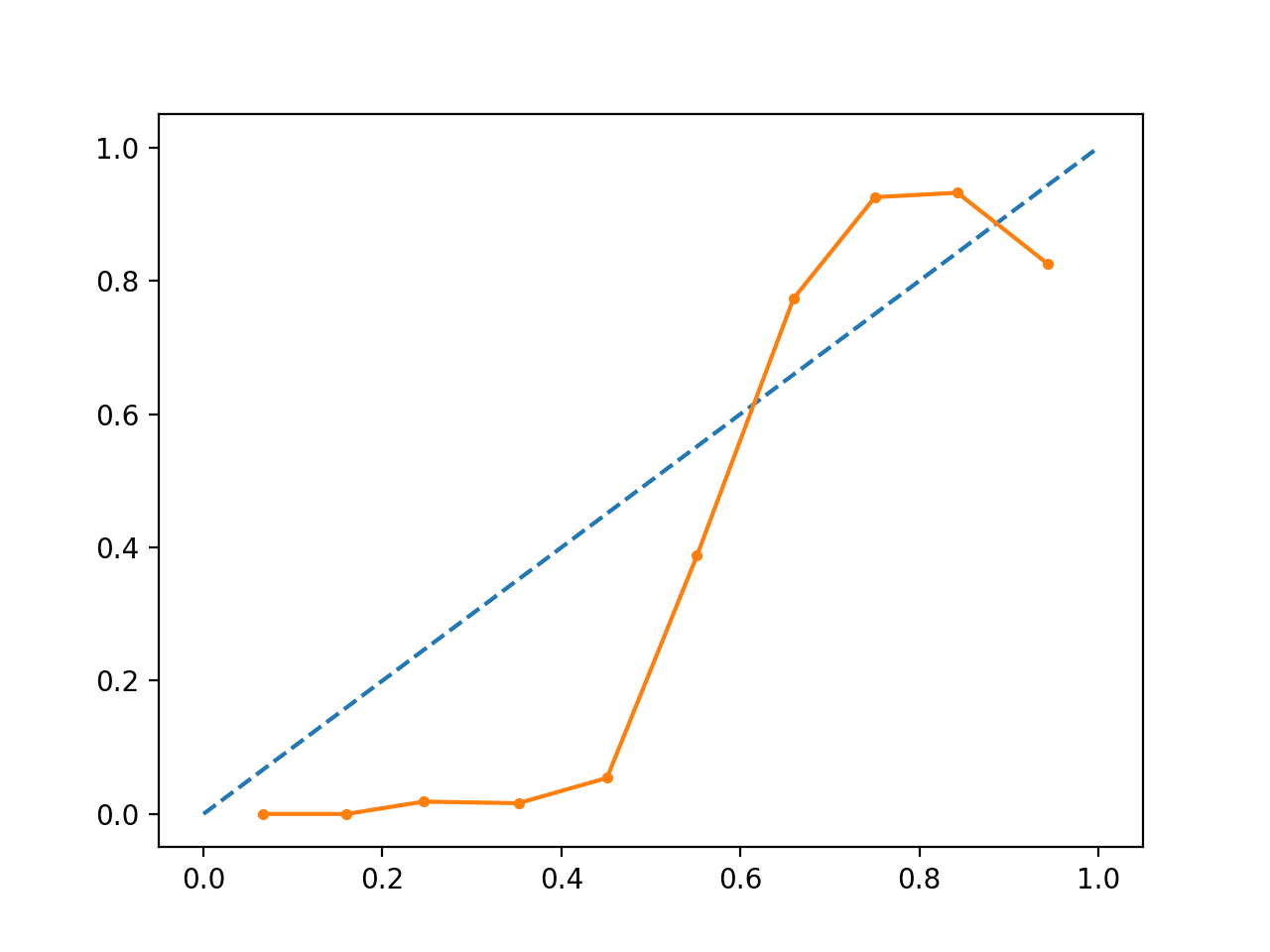
Diagramma di affidabilità SVM non calibrato

Possiamo aggiornare l’esempio per adattare l’SVM tramite la classe CalibratedClassifierCV utilizzando una validazione incrociata di 5 volte, utilizzando i set di holdout per calibrare le probabilità previste.

L’esempio completo è elencato di seguito.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

# Diagramma di affidabilità SVM con calibrazione da sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # dividere in set train/test trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # adatta un modello model = SVC() calibrated = CalibratedClassifierCV(model, method=’sigmoid’, cv=5) calibrated.fit(trainX, trainy) # prevedere le probabilità probs = calibrated.predict_proba(testX) # diagramma di affidabilità fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot perfettamente calibrato pyplot.plot(, , linestyle=’–‘) # traccia l’affidabilità calibrata pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

L’esecuzione dell’esempio crea un diagramma di affidabilità per le probabilità calibrate.

La forma delle probabilità calibrate è diversa, abbracciando la linea diagonale molto meglio, anche se ancora sotto-previsione nel quadrante superiore.

Visualmente, il grafico suggerisce un modello calibrato migliore.

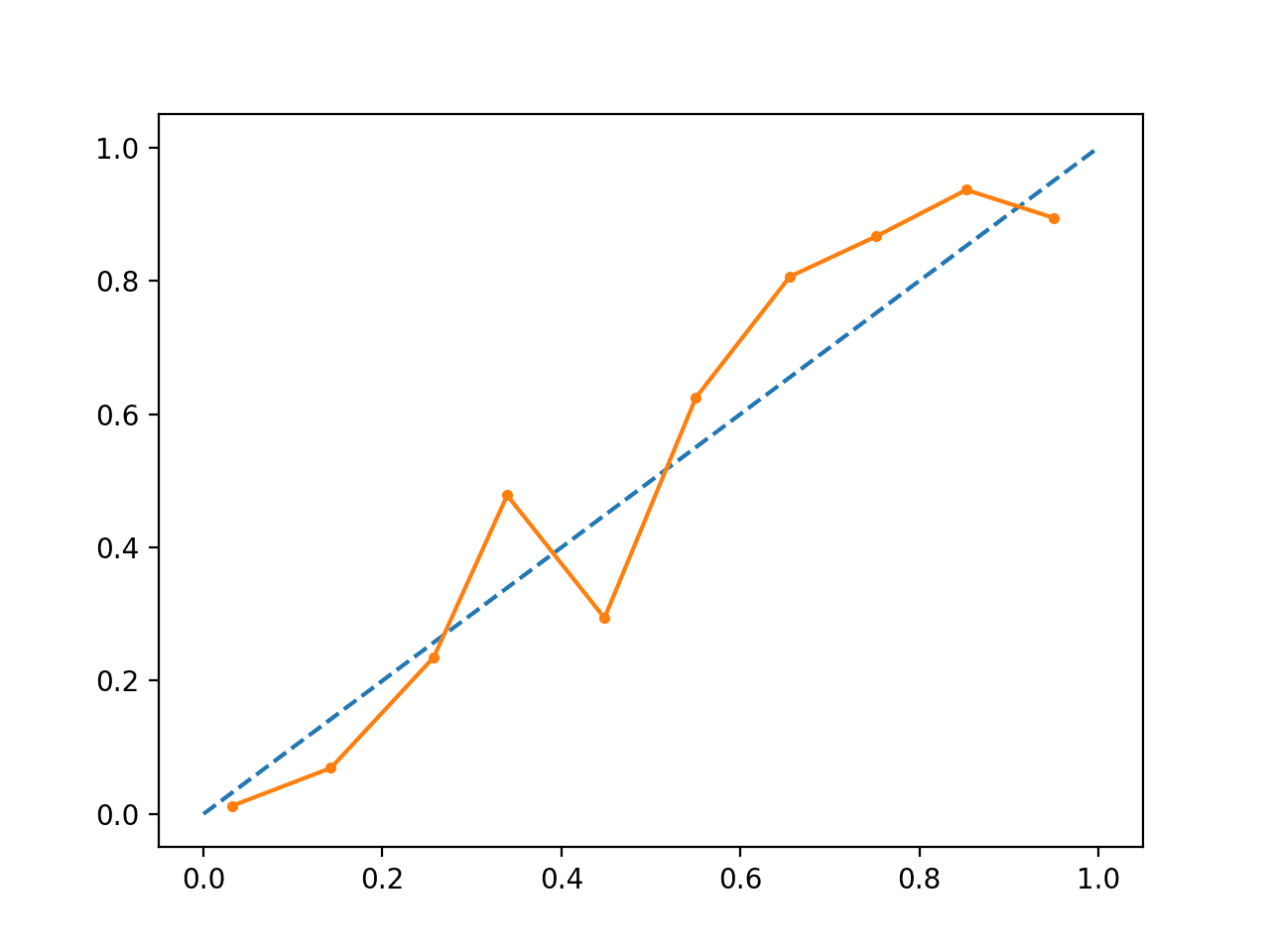
Diagramma di affidabilità SVM calibrato

Possiamo rendere più evidente il contrasto tra i due modelli includendo entrambi i diagrammi di affidabilità sullo stesso grafico.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

# Diagrammi di affidabilità SVM con probabilità non calibrate e calibrate from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # prevedere le probabilità non calibrate def uncalibrated(trainX, testX, trainy): # adatta un modello model = SVC() model.fit(trainX, trainy) # predice le probabilità return model.decision_function(testX) # predice le probabilità calibrate def calibrated(trainX, testX, trainy): # definisce il modello model = SVC() # definisce e adatta il modello di calibrazione calibrated = CalibratedClassifierCV(model, method=’sigmoid’, cv=5) calibrated.fit(trainX, trainy) # predire le probabilità return calibrated.predict_proba(testX) # genera un dataset di 2 classi X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # divide in train/test set trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # previsioni non calibrate yhat_uncalibrated = uncalibrated(trainX, testX, trainy) # previsioni calibrate yhat_calibrated = calibrato(trainX, testX, trainy) # diagrammi di affidabilità fop_uncalibrated, mpv_uncalibrated = calibration_curve(testy, yhat_uncalibrated, n_bins=10, normalize=True) fop_calibrated, mpv_calibrated = calibration_curve(testy, yhat_calibrated, n_bins=10) # plot perfettamente calibrato pyplot.plot(, , linestyle=’–‘, color=’black’) # tracciare le affidabilità del modello pyplot.plot(mpv_uncalibrated, fop_uncalibrated, marker=’.’) pyplot.plot(mpv_calibrated, fop_calibrated, marker=’.’) pyplot.show()

L’esecuzione dell’esempio crea un singolo diagramma di affidabilità che mostra sia le probabilità calibrate (arancione) che quelle non calibrate (blu).

Non è proprio un confronto alla pari poiché le previsioni fatte dal modello calibrato sono in realtà una combinazione di cinque sottomodelli.

Nonostante, vediamo una marcata differenza nell’affidabilità delle probabilità calibrate (molto probabilmente causata dal processo di calibrazione).

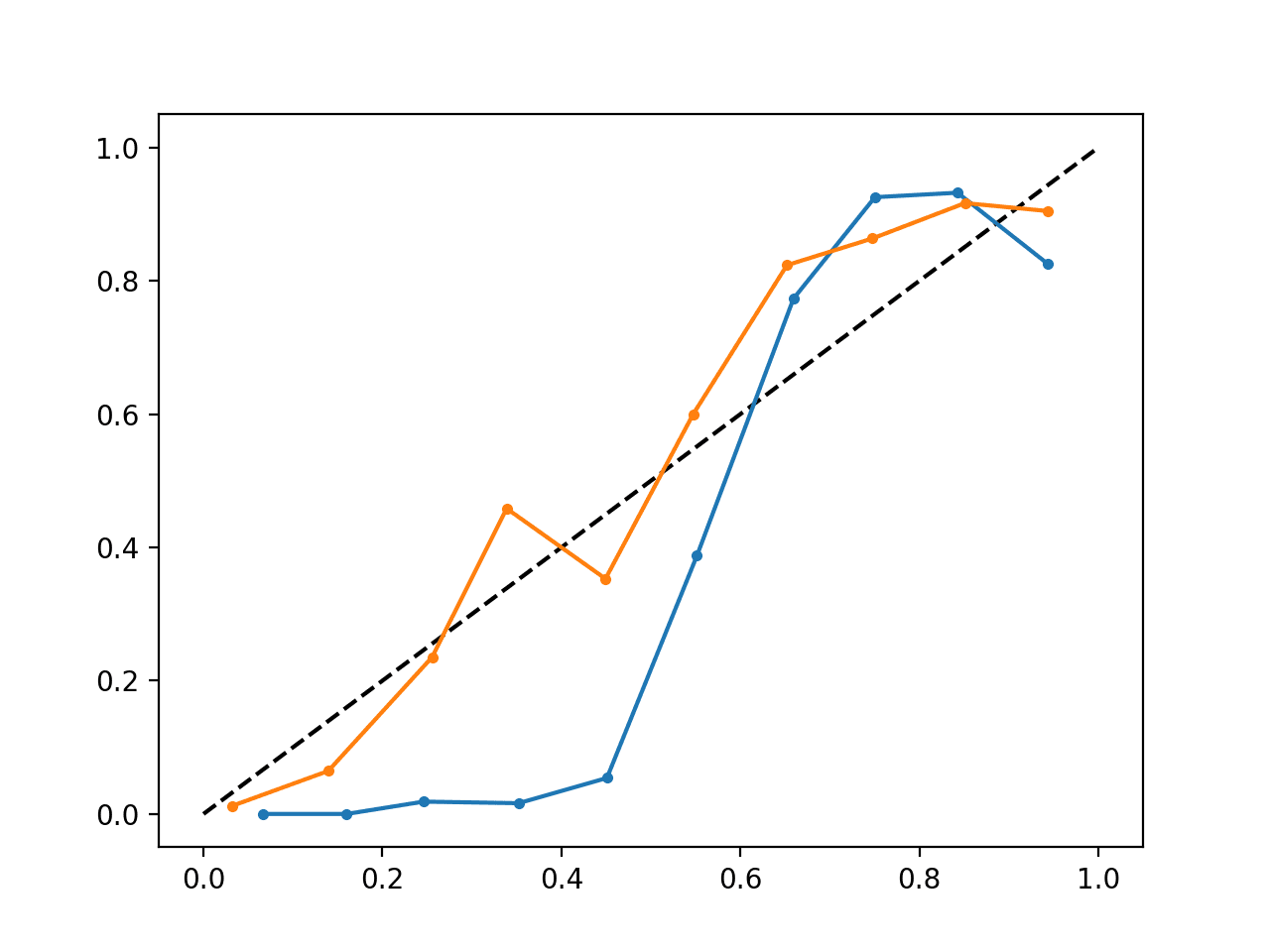
Diagramma di affidabilità SVM calibrato e non calibrato

Altre letture

Questa sezione fornisce altre risorse sull’argomento se vuoi approfondire.

Libri e articoli

• Applied Predictive Modeling, 2013.
• Predicting Good Probabilities With Supervised Learning, 2005.
• Ottenere stime di probabilità calibrate da alberi decisionali e classificatori bayesiani ingenui, 2001.
• Aumentare l’affidabilità dei diagrammi di affidabilità, 2007.

API

• sklearn.calibration.CalibratedClassifierCV API
• sklearn.calibration.calibration_curve API
• Calibrazione della probabilità, scikit-learn User Guide
• Curve di calibrazione della probabilità, scikit-learn
• Confronto della calibrazione dei classificatori, scikit-learn

Articoli

• Sito web di verifica CAWCAR
• Calibrazione (statistica) su Wikipedia
• Classificazione probabilistica su Wikipedia
• Scikit modo corretto di calibrare i classificatori con CalibratedClassifierCV su CrossValidated

Summario

In questo tutorial, hai scoperto l’importanza di calibrare le probabilità previste e come diagnosticare e migliorare la calibrazione dei modelli utilizzati per la classificazione probabilistica.

In particolare, hai imparato:

• Gli algoritmi lineari di apprendimento automatico spesso predicono probabilità di classe non calibrate.
• I diagrammi di affidabilità possono essere usati per diagnosticare la calibrazione di un modello, e i metodi possono essere usati per calibrare meglio le previsioni di un problema.
• Come sviluppare diagrammi di affidabilità e calibrare modelli di classificazione in Python con scikit-learn.

Hai qualche domanda?
Poni le tue domande nei commenti qui sotto e farò del mio meglio per rispondere.

Get a Handle on Probability for Machine Learning!

Develop Your Understanding of Probability

…con poche righe di codice python

Scopri come nel mio nuovo Ebook:
Probability for Machine Learning

Fornisce tutorial di autoapprendimento e progetti end-to-end su:
Teorema di Bayes, Ottimizzazione Bayesiana, Distribuzioni, Massima Probabilità, Cross-Entropia, Calibrazione dei Modelli
e molto altro…

Finalmente sfrutta l’incertezza nei tuoi progetti

Fai a meno degli accademici. Solo risultati. Guarda cosa c’è dentro

Tweet Share Share