Sfondo
La crittografia a curva eclittica (ECC) è un approccio alla crittografia a chiave pubblica, basato sulla struttura algebrica delle curve ellittiche su campi finiti. L’ECC richiede una chiave più piccola rispetto alla crittografia non-ECC per fornire una sicurezza equivalente (una sicurezza ECC a 256 bit ha una sicurezza equivalente raggiunta dalla crittografia RSA a 3072 bit).
Per una migliore comprensione della crittografia a curva ellittica, è molto importante capire le basi della curva ellittica. Una curva ellittica è una curva algebrica planare definita da un’equazione della forma
![]()
dove ‘a’ è il coefficiente di x e ‘b’ è la costante dell’equazione
La curva è non-singolare; cioè il suo grafico non ha cuspidi o autointersecazioni (quando la caratteristica del campo dei coefficienti è uguale a 2 o 3).
In generale, una curva ellittica ha l’aspetto mostrato qui sotto. Le curve ellittiche potrebbero intersecare quasi 3 punti quando si traccia una linea retta che interseca la curva. Come possiamo vedere la curva ellittica è simmetrica intorno all’asse x, questa proprietà gioca un ruolo chiave nell’algoritmo.
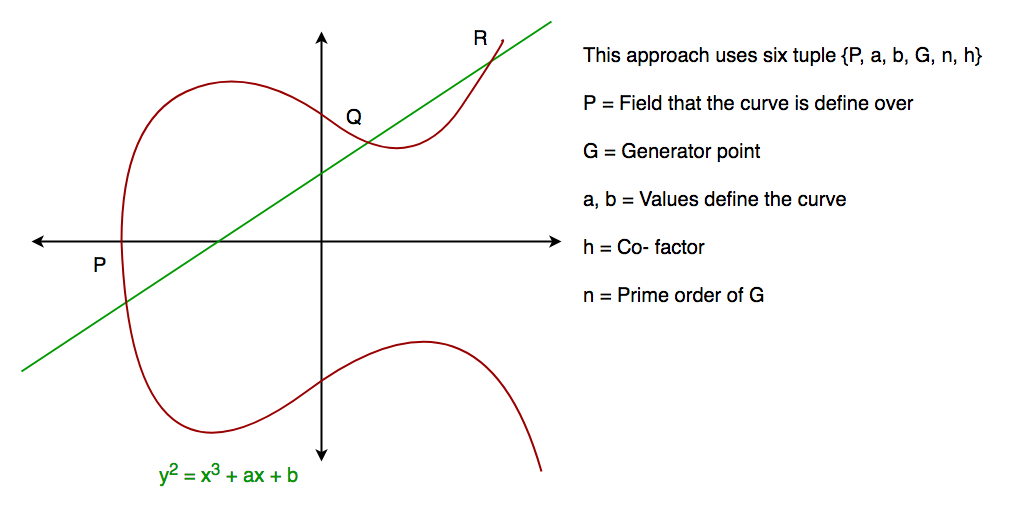
Algoritmo Diffie-Hellman
L’algoritmo Diffie-Hellman viene usato per stabilire un segreto condiviso che può essere usato per comunicazioni segrete durante lo scambio di dati su una rete pubblica usando la curva ellittica per generare punti e ottenere la chiave segreta usando i parametri.
- Per semplicità e implementazione pratica dell’algoritmo, considereremo solo 4 variabili un primo P e G (una radice primitiva di P) e due valori privati a e b.
- P e G sono entrambi numeri disponibili pubblicamente. Gli utenti (diciamo Alice e Bob) scelgono i valori privati a e b e generano una chiave e la scambiano pubblicamente, la persona opposta riceve la chiave e da questa genera una chiave segreta dopo di che hanno la stessa chiave segreta da criptare.
Spiegazione passo dopo passo
| Alice | Bob |
|---|---|
| Chiavi pubbliche disponibili = P, G | Chiavi pubbliche disponibili = P, G |
| Chiave privata selezionata = a | Chiave privata selezionata = b |
|
Key generata =
|
Key generata =
|
| Lo scambio delle chiavi generate avviene | |
| Key ricevuta = y | chiave ricevuta = x |
|
Chiave segreta generata =
|
Chiave segreta generata =
|
|
Algebricamente si può dimostrare che
|
|
| Gli utenti hanno ora una chiave segreta simmetrica da criptare | |
Esempio
Step 1: Alice and Bob get public numbers P = 23, G = 9Step 2: Alice selected a private key a = 4 and Bob selected a private key b = 3Step 3: Alice and Bob compute public valuesAlice: x =(9^4 mod 23) = (6561 mod 23) = 6 Bob: y = (9^3 mod 23) = (729 mod 23) = 16Step 4: Alice and Bob exchange public numbersStep 5: Alice receives public key y =16 and Bob receives public key x = 6Step 6: Alice and Bob compute symmetric keys Alice: ka = y^a mod p = 65536 mod 23 = 9 Bob: kb = x^b mod p = 216 mod 23 = 9Step 7: 9 is the shared secret.
Implementazione:
#include<stdio.h>#include<math.h>longlongintpower(longlonginta, longlongintb, longlongintP) { if(b == 1) returna; else return(((longlongint)pow(a, b)) % P); }intmain() { longlongintP, G, x, a, y, b, ka, kb;
P = 23; printf("The value of P : %lld\n", P); G = 9; printf("The value of G : %lld\n\n", G); a = 4; printf("The private key a for Alice : %lld\n", a); x = power(G, a, P); b = 3; printf("The private key b for Bob : %lld\n\n", b); y = power(G, b, P); ka = power(y, a, P); kb = power(x, b, P); printf("Secret key for the Alice is : %lld\n", ka); printf("Secret Key for the Bob is : %lld\n", kb);
return0; }fromrandom importrandint if__name__ =='__main__': P =23 G =9 print('The Value of P is :%d'%(P)) print('The Value of G is :%d'%(G)) a =4 print('The Private Key a for Alice is :%d'%(a)) x =int(pow(G,a,P)) b =3 print('The Private Key b for Bob is :%d'%(b))
y =
int(pow(G,b,P))
ka =
int(pow(y,a,P)) kb =int(pow(x,b,P)) print('Secret key for the Alice is : %d'%(ka)) print('Secret Key for the Bob is : %d'%(kb)) Output
The value of P : 23The value of G : 9The private key a for Alice : 4The private key b for Bob : 3Secret key for the Alice is : 9Secret Key for the Bob is : 9
Questo articolo è stato contribuito da Souvik Nandi. Se ti piace GeeksforGeeks e vuoi contribuire, puoi anche scrivere un articolo usando contribute.GeeksforGeeks.org o inviare il tuo articolo a [email protected]. Vedi il tuo articolo apparire sulla pagina principale di GeeksforGeeks e aiuta altri Geek.
Si prega di scrivere commenti se trovi qualcosa di errato, o se vuoi condividere ulteriori informazioni sull’argomento trattato sopra.