قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).

Definizione

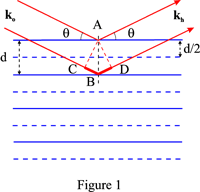
La legge di Bragg fornisce la condizione perché un’onda piana sia diffratta da una famiglia di piani reticolari:

2 d sin θ = n λ

dove d è la spaziatura interplanare, θ l’angolo tra il vettore dell’onda piana incidente, ko, e i piani del reticolo, λ la lunghezza d’onda e n è un intero, l’ordine della riflessione. È equivalente alla condizione di diffrazione nello spazio reciproco e alle equazioni di Laue.

Derivazione diretta della legge di Bragg

• Riflessione dal primo piano

Le onde diffuse saranno in fase qualunque sia la distribuzione dei punti di diffusione nel primo piano se l’angolo del vettore dell’onda riflessa, kh, è anche uguale a θ. Questa è la legge di riflessione di Snell-Descartes.

• Riflessione dal secondo piano

Siccome la fase delle onde riflesse è indipendente dalla posizione del punto di diffusione nel piano, la differenza di fase tra le onde riflesse da due piani successivi del reticolo si ottiene scegliendo arbitrariamente un punto di diffusione, A, sul primo piano e un punto di diffusione, B, sul secondo piano tale che AB sia normale ai piani. Se C e D sono le proiezioni di A sui vettori d’onda incidente e riflessa che passano per B, è chiaro dalla figura 1 che la differenza di percorso tra le onde riflesse in A e B, rispettivamente, è:

CB + BD = 2d sin θ

e che le due onde saranno in fase se questa differenza di percorso è uguale a nλ dove n è un intero.

• Riflessione dal terzo piano, ecc. piani

Se la relazione di Bragg è soddisfatta per i primi due piani, le onde riflesse con vettore d’onda kh saranno in fase per tutti i piani della famiglia.

Ordine della riflessione

La legge di Bragg può anche essere scritta:

2 (d/n) sin θ = λ.

Si può quindi dire che una riflessione di Bragg di ordine n su una famiglia di piani di reticolo di ordine n è equivalente alla riflessione di ordine 1 su una famiglia di piani fittizi, o immaginari, di spaziatura del reticolo

d_{hkl} = d/n.

Questa famiglia fittizia è associata al vettore reticolo reciproco OH dove OH = n/d = 1/d_{hkl}. Gli indici di riflessione sono hkl. Per esempio, le linee orizzontali tratteggiate nella figura 1 corrispondono ai piani fittizi associati al secondo ordine, n = 2.

Condizioni di riflessione

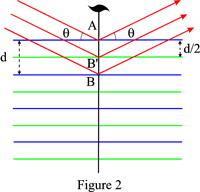
Se c’è un piano di scorrimento o un asse a vite normale ai piani del reticolo, la distanza dei piani riflettenti effettivi è d/2 per un piano di scorrimento e (d p/q) per un asse a vite qp. La legge di Bragg dovrebbe quindi essere scritta:

2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ

per un piano di scorrimento e

2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ

per un asse di vite qp.

Le riflessioni di ordine dispari per un piano di scorrimento e di ordine diverso da (q/p)n per un asse di vite sono allora assenti. Si parla di assenze sistematiche legate alla presenza di componenti di scorrimento o di vite.

A titolo di esempio, la figura 2 mostra il caso di un asse a vite 21: i piani riflettenti sono i piani blu e i piani verdi dedotti da questi ultimi dall’azione dell’asse a vite. Le riflessioni di ordine dispari saranno sistematicamente assenti.

Influenza della deformazione

Una deformazione che lascia una famiglia di piani reticolari (hkl) indistorta e la sua spaziatura reticolare d invariata non influenzerà l’angolo di Bragg delle riflessioni kkl, ad es.

Storia

Bragg (1890-1971) presentò la sua derivazione della condizione di riflessione ad una riunione della Cambridge Philosophical Society l’11 novembre 1912. Il suo articolo fu pubblicato nel 1913. Per i dettagli, vedi P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Sezione 5, p. 64 e A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Sezione 6.11, p. 120.

Vedi anche

• Equazioni di Laue