Tassi di errore familiari > Metodo Holm-Metodo Bonferroni

Potresti voler leggere prima questo articolo: Familywise Error Rates.

Che cos’è il Metodo Holm-Bonferroni?

Il Metodo Holm-Bonferroni (chiamato anche Procedura Sequenziale Bonferroni di Holm) è un modo per trattare i tassi di errore familiari (FWER) per i test di ipotesi multiple. È una modifica della correzione Bonferroni. La correzione Bonferroni riduce la possibilità di ottenere un risultato statisticamente significativo (cioè un errore di tipo I) quando si eseguono test multipli. Anche se il Bonferroni è semplice da calcolare, soffre di una mancanza di potenza statistica. Anche il metodo Holm-Bonferroni è abbastanza semplice da calcolare, ma è più potente del Bonferroni a passo singolo.

Formula

La formula per calcolare l’Holm-Bonferroni è: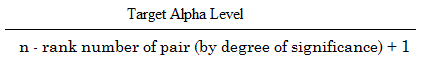

dove:

• Livello alfa obiettivo = livello alfa complessivo (di solito .05),
• n = numero di test.

Il prossimo esempio mostra come funziona la formula.

Esempio

Questione: Usa il metodo Holm-Bonferroni per testare le seguenti quattro ipotesi e i loro valori p associati ad un livello alfa di .05:

• H1 = 0.01.
• H2 = 0.04
• H3 = 0.03
• H4 = 0.005

Nota: conosciamo già i valori p associati ad ogni ipotesi. Se non conoscete i p-valori, eseguite un test per ogni ipotesi prima di tentare di regolare il FWER usando il metodo Holm-Bonferroni.

Step 1: Ordinate i p-valori dal più piccolo al più grande:

• H4 = 0.005
• H1 = 0,01
• H3 = 0,03
• H2 = 0,04

Step 2: lavorare la formula di Holm-Bonferroni per il primo rango:
HB = Target α / (n – rango + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Step 3: Confrontare il p-value del primo rango (il più piccolo) dal passo 1 al livello alfa calcolato nel passo 2:
Più piccolo p-value, nel passo 1 (H4 = 0.005) < Livello alfa nel Passo 2 (.0125).
Se il p-value è più piccolo, rifiutare l’ipotesi nulla per questo test individuale.

Il p-value di .005 è inferiore a .0125, quindi l’ipotesi nulla per H4 è rifiutata.

Passo 4: Ripetere la formula HB per il secondo grado.
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

Step 5: Confrontare il risultato della formula HB del passo 4 con il p-value del secondo rango:
Secondo classificato p-value, nel Passo 1 (H1 = 0.01) < Livello alfa nel Passo 2 (.0167).
Il p-value di .01 è inferiore a .0167, quindi anche l’ipotesi nulla per H1 è rifiutata.

Passo 6: Ripetere la formula HB per il terzo rango.
HB = Target α / (n – rango + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

Passo 7: Confrontare il risultato della formula HB del passo 6 con il p-value del terzo rango:
Il p-valore del terzo classificato, nel Passo 1 (H3 = 0.03) > Livello alfa nel Passo 6 (.025).
Il p-value di .03 è maggiore di .025, quindi l’ipotesi nulla per H3 non è respinta.

Il test si ferma quando si raggiunge la prima ipotesi non respinta. Tutte le ipotesi successive sono non significative (cioè non respinte).

Riferimento:
Holm, S. 1979. Una semplice procedura di test multiplo sequenziale reiettiva. Scandinavian Journal of Statistics 6:65-70

——————————————————————————

Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!