Questo è un vettore:

Un vettore ha magnitudine (dimensione) e direzione:
La lunghezza della linea mostra la sua magnitudine e la punta della freccia indica la direzione.
Possiamo sommare due vettori unendoli testa-coda:
E non importa in quale ordine li sommiamo, otteniamo lo stesso risultato:
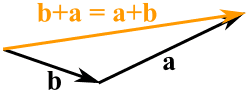
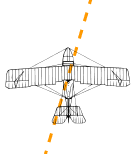
Esempio: Un aereo sta volando, puntando verso Nord, ma c’è un vento che viene da Nord-Ovest.
I due vettori (la velocità causata dall’elica, e la velocità del vento) danno come risultato una velocità al suolo leggermente più lenta in direzione un po’ più a Est del Nord.
Se tu guardassi l’aereo da terra sembrerebbe che stia scivolando un po’ lateralmente.
Hai mai visto accadere questo? Forse avete visto uccelli che lottano contro un forte vento e che sembrano volare di lato. I vettori aiutano a spiegarlo.
Velocità, accelerazione, forza e molte altre cose sono vettori.
Sottrarre
Possiamo anche sottrarre un vettore da un altro:
- prima invertiamo la direzione del vettore che vogliamo sottrarre,
- poi li sommiamo come al solito:
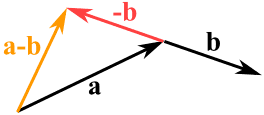
a – b
Notazione
Un vettore è spesso scritto in grassetto, come a o b.
| Un vettore può anche essere scritto come le lettere di testa e di coda con una freccia sopra, così: |
 |
Calcoli
Ora …. come facciamo i calcoli?
Il modo più comune è quello di scomporre prima i vettori in parti x e y, come questo:
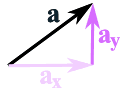
Il vettore a viene scomposto in
i due vettori ax e ay
(Vediamo dopo come fare questo.)
Addizione di vettori
Possiamo quindi sommare i vettori sommando le parti x e sommando le parti y:
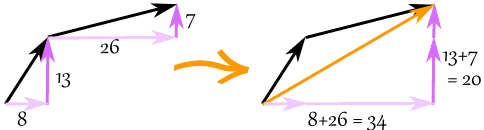
Il vettore (8, 13) e il vettore (26, 7) si sommano al vettore (34, 20)
esempio: sommare i vettori a = (8, 13) e b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Quando dividiamo un vettore in questo modo, ogni parte è chiamata componente:
Sottrarre i vettori
Per sottrarre, prima invertiamo il vettore che vogliamo sottrarre, poi aggiungiamo.
Esempio: sottrarre k = (4, 5) da v = (12, 2)
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
Magnitudine di un vettore
La magnitudine di un vettore è indicata da due barre verticali ai lati del vettore:
|a|
O si può scrivere con due barre verticali (per non confonderlo con il valore assoluto):
||a||
Usiamo il teorema di Pitagora per calcolarlo:
a| = √( x2 + y2 )
Esempio: qual è la grandezza del vettore b = (6, 8) ?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Un vettore con magnitudine 1 è chiamato vettore unitario.
Vettore vs scalare
Uno scalare ha solo magnitudine (grandezza).
Scalare: solo un numero (come 7 o -0.32) .. sicuramente non un vettore.
Un vettore ha grandezza e direzione, ed è spesso scritto in grassetto, così sappiamo che non è uno scalare:
- quindi c è un vettore, ha grandezza e direzione
- ma c è solo un valore, come 3 o 12.4
Esempio: kb è in realtà lo scalare k per il vettore b.
Moltiplicando un vettore per uno scalare
Quando moltiplichiamo un vettore per uno scalare si chiama “scalare” un vettore, perché cambiamo quanto è grande o piccolo il vettore.
Esempio: moltiplicare il vettore m = (7, 3) per lo scalare 3
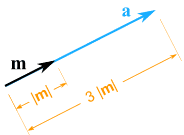 |
a = 3m = (3×7, 3×3) = (21, 9) |
Punta ancora nella stessa direzione, ma è 3 volte più lungo
(E ora sai perché i numeri si chiamano “scalari”, perché “scalano” il vettore in alto o in basso.)
Moltiplicare un vettore per un altro vettore (prodotto puntiforme e prodotto incrociato)
 |
Come si moltiplicano due vettori insieme? C’è più di un modo!
(Leggi queste pagine per maggiori dettagli.) |
Più di 2 dimensioni
I vettori funzionano perfettamente anche in 3 o più dimensioni:
Il vettore (1, 4, 5)
Esempio: sommare i vettori a = (3, 7, 4) e b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
esempio: qual è la grandezza del vettore w = (1, -2, 3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9) = √14
Ecco un esempio a 4 dimensioni (ma è difficile da disegnare!):
Esempio: sottrarre (1, 2, 3, 4) da (3, 3, 3, 3)
(3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3, 3) + (-1,-2,-3,-4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Magnitudine e direzione
Possiamo conoscere la grandezza e la direzione di un vettore, ma vogliamo le sue lunghezze x e y (o viceversa):
 |
<> |  |
| Vettore a in coordinate polari | Vettore a in coordinate cartesiane |
Puoi leggere come convertirli in Coordinate polari e cartesiane, ma ecco un rapido riassunto:
| Dalle coordinate polari (r,θ) alle coordinate cartesiane (x,y) |
Dalle coordinate cartesiane (x,y) alle coordinate polari (r,θ) |
|
|---|---|---|
|
|
Un esempio
Sam e Alex stanno tirando una scatola.
- Sam tira con 200 Newton di forza a 60°
- Alex tira con 120 Newton di forza a 45° come mostrato
Qual è la forza combinata, e la sua direzione?
Sommiamo i due vettori testa a coda:
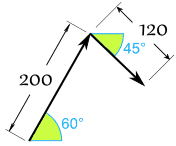
Prima convertiamo da polare a cartesiano (a 2 decimali):
Vettore di Sam:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21
Vettore di Alex:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84.85
Ora abbiamo:
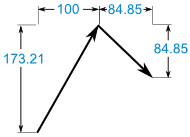
Somma:
(100, 173.21) + (84.85, -84.85) = (184.85, 88.36)
Questa risposta è valida, ma riconvertiamo in polare dato che la domanda era in polare:
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88.36 / 184.85 ) = 25.5°
E abbiamo questo risultato (arrotondato):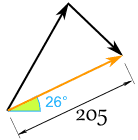
E appare così per Sam e Alex:
Potrebbero ottenere un risultato migliore se fossero spalla a spalla!





