Familywise Error Rates > Holm-。Bonferroni法
まずこの記事を読んでみてはいかがでしょうか。
Holm-Bonferroni法とは
Holm-Bonferroni法(Holm’s Sequential Bonferroni Procedureとも呼ばれる)は、多重仮説検定の家族単位の誤り率(FWER)を扱うための方法です。 これは、ボンフェローニ補正の修正です。 ボンフェローニ補正は、複数の検定を実行する際に、統計的に有意な結果(すなわち、第一種エラー)を得る可能性を低減します。 Bonferroniは計算が簡単ですが、統計的検出力が不足しています。 Holm-Bonferroni法も計算はかなり簡単ですが、シングルステップのBonferroniよりも強力です。
計算式
Holm-Bonferroniを計算する式は以下の通りです。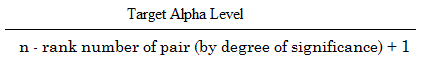
Where:
- 目標のアルファレベル=全体のアルファレベル(通常は.05)、
- n = テストの数
次の例では、この式がどのように機能するかを示します。
Example
質問です。 以下の4つの仮説とそれに関連するp値をアルファレベル0.05で検定するために、Holm-Bonferroni法を使用してください:
- H1 = 0.01.
- H2 = 0.04
- H3 = 0.03
- H4 = 0.005
注:各仮説に関連するp値はすでにわかっています。 p値がわからない場合は、Holm-Bonferroni法を使用してFWERを調整しようとする前に、各仮説に対するテストを実行してください。
Step 1: p値を小さいものから大きいものに並べる:
- H4 = 0.
- H4 = 0.005
- H1 = 0.01
- H3 = 0.03
- H2 = 0.04
Step 2: Holm-Bonferroniの公式を第1ランクに適用する:
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.Step 3: Step 1の1位の(最も小さい)p値をStep 2で計算したαレベルと比較します:
Smallest p-value, in Step 1 (H4 = 0. 005).005) < Step2のαレベル(.0125)
p値が小さければ、この個別テストの帰無仮説を棄却します。p値0.005は0.0125より小さいので、H4の帰無仮説は棄却されます。
Step 4: HBの式を2番目のランクについて繰り返します。
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167Step 5: Step 4のHB式の結果と、2位のp値を比較します。
2位のp値は、Step1(H1 = 0.01)< Step2のαレベル(.0167)
p値の.01は.0167より小さいので、H1の帰無仮説も棄却されます。Step 6: HB式を3位まで繰り返します。
HB = Target α / (n – rank + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025Step 7: Step 6のHB式の結果と、3位のp値を比較します。
3位のp値、Step1で(H3 = 0.03) > Step6のアルファレベル(.025)
p値0.03は0.025より大きいので、H3の帰無仮説は棄却されません。最初の非棄却仮説に到達した時点で、検定は停止します。
参考文献:
Holm, S. 1979. シンプルな逐次棄却型多重検定の手順。 Scandinavian Journal of Statistics 6:65-70CITE THIS AS:
Stephanie Glen. “Holm-Bonferroni Method: Step by Step” From StatisticsHowTo.com: 初歩的な統計学の知識を得ることができます。 https://www.statisticshowto.com/holm-bonferroni-method/——————————————————————————
宿題やテストの問題で助けが必要ですか? Chegg Studyでは、その分野の専門家があなたの質問にステップバイステップで解決策を提示します。 Cheggチューターとの最初の30分は無料です。