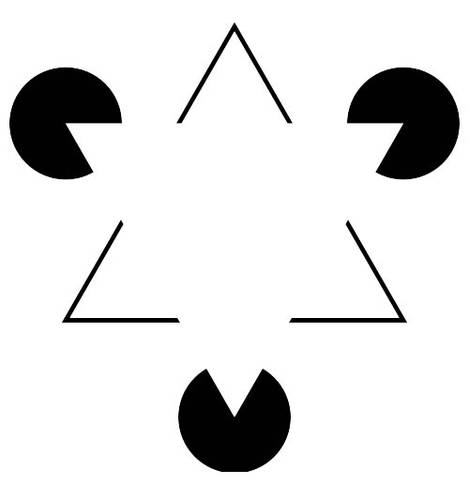
1955年にイタリアの心理学者ガエタノ・カニッツァが考案した「カニッツァ・トライアングル」は、錯視的な輪郭の典型的な例です。 上の画像のように、三角形を示す明確な線や囲まれた空間がないにもかかわらず、白い正三角形がはっきりと認識されます。
ゲシュタルト心理学者は、カニッツァトライアングルを使って、「グループ化されたオブジェクトは全体として見られる」という閉鎖の法則を説明しています。 つまり、私たちは、物体が不完全であっても全体として認識し、隙間を無視したり、輪郭線を完成させたりして、見慣れた図や形を形成しているのです。
「カニッツァの三角形の錯視」では、実際には円も三角形もないのに、3つの黒い円と2つの三角形を容易に認識することができます。 私たちはそれ以上のものを見ているのです。 私たちは、実際には存在しない物体を知覚しているのです。 “
「3つの別々の『パックマン』を1つの全体の一部として見る全体論的な視覚によってのみ、私たちは三角形を知覚することができる」(Simmons, 1996)
。