Learning Objectives
- damped harmonic motionの動きを説明する
- damped harmonic oscillationsの運動方程式を書く
- driven.or forced, damped harmonic motionの動きを説明する。
現実の世界では、振動が真のSHMに従うことはほとんどありません。 通常、何らかの摩擦が運動を減衰させるために作用し、その結果、振動が消滅するか、継続するためにはより大きな力が必要になります。
ギターの弦は、弾いてから数秒後には振動しなくなります。
ギターの弦は弾くと数秒後には振動しなくなります。 摩擦やその他の非保存的な力を小さくしたり無視したりすることはよくありますが、完全に減衰しない運動というのは稀です。

図は、質量mが力定数kのばねに取り付けられている状態です。 質量は、粘性のある流体の中で平衡位置の周りを振動しますが、振幅は振動するたびに小さくなります。 ダンピング量が少ないシステムでは、周期と周波数は一定で、SHMとほぼ同じですが、振幅は図のように徐々に小さくなります。
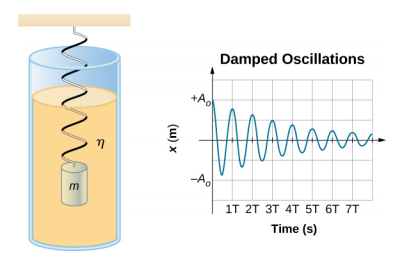
質量に作用する力を考えてみましょう。 この章の前半で説明したように、重りの唯一の寄与は平衡位置を変えることであることに注意してください。 したがって、正味の力は、ばねの力と減衰力(F_D\)になります。 速度の大きさが小さく、質量がゆっくりと振動する場合は、減衰力は速度に比例し、運動方向に対して作用します(˶ˆ꒳ˆ˵)。 したがって、質量にかかる正味の力は
これをxの微分方程式として書くと
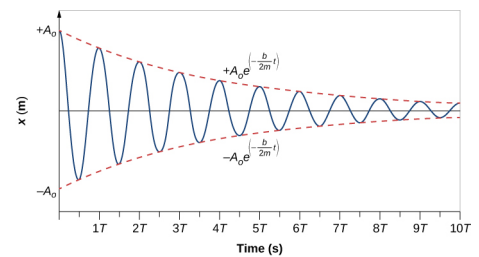
この方程式の解を求めるために、図(˶‾᷄ -̫ ‾᷅˵)のような位置と時間のプロットを考えてみましょう。 この曲線は、指数関数の包絡線の中で振動する余弦曲線のように見えます。 解答は
これが実際に解答であることを証明することが課題となります。 正しい解であることを証明するために、時間に関する1次および2次の導関数を取り、式15.23に代入します。
SHMを受ける質量の角周波数は、力の定数の平方根を質量で割ったものに等しいことを思い出してください。 これはしばしば固有角周波数と呼ばれ、次のように表されます
減衰調和運動の角周波数は
減衰調和運動の説明を始めたときに、減衰が小さくなければならないと述べたことを思い出してください。 ここで2つの疑問が浮かびます。 なぜダンピングを小さくしなければならないのか? また、小さいとはどの程度の大きさなのか? システムの減衰量を徐々に増やしていくと、周期と周波数に影響が出始めます。これは、減衰が前後の動きに逆らって、それを遅くするためです。 ダンピングが非常に大きい場合、システムは振動すらせず、ゆっくりと平衡状態に向かっていきます。 角周波数は次のようになります。
bが大きくなると、\frac{k}{m} – \left(dfrac{b}{2m}\right)^{2}\が小さくなり、最終的にはb = \sqrt{4mk}\でゼロになります。 bがこれ以上大きくなると、\(\frac{k}{m} – \left(hardfrac{b}{2m}\right)^{2}\)は負の数となり、\(sqrt{\frac{k}{m} – \left(hardfrac{b}{2m}\right)^{2}\)は複素数となります。
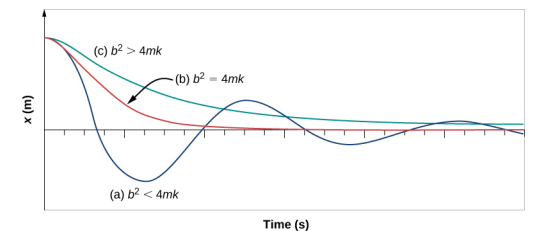
図は、ダンピング量を変えたときの調和振動子の変位を示したものです。
- 減衰定数b < が小さいとき、系は振動しながらも運動の振幅は指数関数的に減衰していきます。 この系は、曲線(a)のようにアンダーダンピングされているといいます。 多くの系はアンダーダンピングであり、質量がバネの上で振動するように、振幅が指数関数的に減少しながら振動します。
- 減衰定数が\\であれば、曲線(b\)のように、臨界減衰と呼ばれます。 臨界減衰系の例としては、自動車のショックアブソーバーなどが挙げられます。 振動はできるだけ早く減衰したほうが有利です。
- 図の曲線(c)は、オーバーダンピングされた系を表していますが、ここでは b > ²sqrt{4mk}\ となっています。
臨界的なダンピングが望まれるのは、そのようなシステムが急速に平衡に戻り、同様に平衡状態を維持するからです。
Exercise ˶‾᷅˵
完全に減衰していない調和振動子は、なぜそれほど珍しいのでしょうか?
Contributors and Attributions
-
Samuel J. Ling (Truman State University)、Jeff Sanny (Loyola Marymount University)、Bill Moebsをはじめとする多くの寄稿者がいます。 この作品はOpenStax University Physicsによって、クリエイティブ・コモンズ表示ライセンス(by 4.0)の下でライセンスされています。