A Step by Step Backpropagation Example - Matt Mazur

Background

バックプロパゲーションは、ニューラルネットワークをトレーニングするための一般的な方法です。バックプロパゲーションがどのように機能するかを説明しようとする論文には事欠きませんが、実際の数値を示した例を含むものはほとんどありません。

Backpropagation in Python

バックプロパゲーションアルゴリズムを実装するために私が書いた Python スクリプトは、この Github レポで遊ぶことができます。

Backpropagation Visualization

学習中のニューラルネットワークを示すインタラクティブなビジュアライゼーションについては、私の Neural Network visualization をご覧ください。

Overview

このチュートリアルでは、2つの入力、2つの隠れニューロン、2つの出力ニューロンを持つニューラルネットワークを使用します。さらに、隠れニューロンと出力ニューロンにはバイアスが含まれています。

基本的な構造は以下のとおりです。

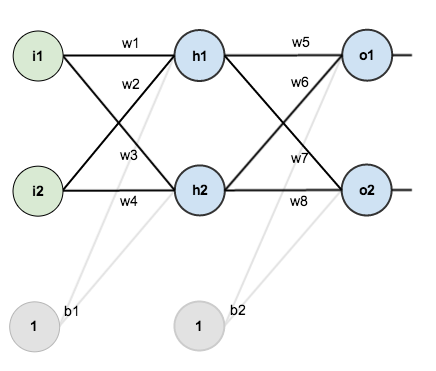
neural_network (7)

作業に必要な数を得るために、初期の重み、バイアス、トレーニング用の入力/出力を示します。

neural_network (9)

バックプロパゲーションの目的は、ニューラルネットワークが任意の入力を出力に正しくマッピングする方法を学習できるように、重みを最適化することです。

このチュートリアルの残りの部分では、単一のトレーニングセットを使用します: 入力 0.05 および 0.10 が与えられた場合、ニューラルネットワークに 0.01 および 0.99 を出力させます。

各隠れ層のニューロンへの純入力の合計を計算し、活性化関数 (ここではロジスティック関数を使用) を使用して純入力の合計を潰し、出力層のニューロンでこのプロセスを繰り返します。

総合正味入力は、一部の資料では単なる正味入力とも呼ばれています。

ここでは、 $h_1$ の総純入力を計算する方法を説明します。

$net_{h1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1$

$net_{h1} = 0.15 * 0.05 + 0.2 * 0.1 + 0.35 * 1 = 0.3775$

続いて、ロジスティック関数を用いて、 $h_1$ の出力を得ます：

$out_{h1} = ″frac{1}{1+e^{-net_{h1}}″ = ″frac{1}{1+e^{-0.3775}} = 0.593269992$

$h_2$ についても同様の処理を行うと次のようになります。596884378

隠れ層のニューロンからの出力を入力として、出力層のニューロンにこのプロセスを繰り返します。

以下は $o_1$ の出力です。 + W_6 * OUT_{H2}.. + b_2 * 1

$net_{o1} = 0.4 * 0.593269992 + 0.45 * 0.596884378 + 0.6 * 1 = 1.105905967$

$out_{o1} = ˶frac{1}{1+e^{-net_{o1}}} = ˶frac{1}{1+e^{-1.105905967}} = 0.75136507$

そして、 $o_2$ についても同様の処理を行うと次のようになります。

$out_{o2} = 0.772928465$

総合誤差の計算

ここで、二乗誤差関数を使って各出力ニューロンの誤差を計算し、それらを合計して総合誤差を得ることができます。

$E_{total} = sum ˶ˆ꒳ˆ˵ (target - output)^{2}$

ある資料では、ターゲットを理想、アウトプットを実際と呼んでいます。

$\frac{1}{2}$ が含まれているのは、後に微分する際に指数がキャンセルされるためです。

例えば、 $o_1$ の目標出力は0.

$E_{o1} = ˶ˆ꒳ˆ˵ (target_{o1} - out_{o1})^{2} = ˶ˆ꒳ˆ˵ (target_{o1} - out_{o1})^{2} = ˶ˆ꒳ˆ˵ (0.01 - 0.75136507)^{2} = 0.274811083$

このプロセスを $o_2$ （ターゲットが0.99であることを覚えておく）に対して繰り返すと、次のようになります。99であることを覚えておいてください）では次のようになります。

$E_{o2} = 0.023560026$

ニューラルネットワークのトータルエラーは、これらのエラーの合計です。 + E_{o2} = 0.274811083 + 0.023560026 = 0.298371109

バックワードパス

バックプロパゲーションの目的は、実際の出力が目標出力に近づくようにネットワーク内の各重みを更新することで、各出力ニューロンおよびネットワーク全体の誤差を最小化することです。

出力層

$w_5$ について考えてみましょう。

$w_5$ $frac{\\ E_{total}}{\ w_{5}}$ ）にどれだけ影響するかを知りたいのです。

$¥frac{\\ E_{total}}{\ w_{5}}$ $E_{total}$ $w_{5}$ $w_{5}$ を基準とした勾配」とも言えます。

連鎖律を適用すると次のようになります。

$\frac{\partial E_{total}}{\partial w_{5}} = \frac{\partial E_{total}}{\partial out_{o1}} * \frac{\partial out_{o1}}{\partial net_{o1}} * \frac{\partial net_{o1}}{\partial w_{5}}$ $\\ E_{total}}{\ w_{5}} = ˶ˆ꒳ˆ˵ ) * ˶ˆ꒳ˆ˵ )$

output_1_backprop (4)

この式の各部分を把握する必要があります。

まず、トータルエラーは出力に対してどのくらい変化するのでしょうか？

$E_{total} = ˶frac{1}{2}(target_{o1} - out_{o1})^{2}. + ¶frac{1}{2}(target_{o2} - out_{o2})^{2}$

$E_{total}}{ ¶partial out_{o1}} = 2 * ¶frac{1}{2}(target_{o1} - out_{o1})^{2 - 1}. * -1 + 0$

$-(target - out)$ $out - target$

総合誤差を $out_{o1}$ $out_{o1}$ $out_{o1}$ $量$ rac{1}{2}(target_{o2} – out_{o2})^{2}

はゼロとなり、ゼロである定数の微分を取っていることになります。

次に、 $o_1$ の出力は、その総正味入力に対してどのくらい変化するでしょうか。

ロジスティック関数の偏微分は、出力に1をかけたものから出力を引いたものになります。

$out_{o1} = ˶frac{1}{1+e^{-net_{o1}}}$

$˶frac{˶frac out_{o1}}{˶frac net_{o1}} = out_{o1}(1 - out_{o1}) = 0.75136507(1 - 0.75136507) = 0.186815602$

最後に、 $o1$ $w_5$ に対してどのくらい変化するでしょうか。

$net_{o1} = w_5 * out_{h1}. + W_6 * OUT_{H2}. + b_2 * 1$

$\frac{partial net_{o1}}{\partial w_{5}} = 1 * out_{h1}. * w_5^{(1 - 1)} + 0 + 0 = out_{h1} = 0.593269992$

Putting it all:

$\frac{˶E_{total}}{\frac w_{5}} = ˶E_{total}}{\frac out_{o1}}. * ˶ˆ꒳ˆ˵ )$

$\frac{partial E_{total}}{\frac{w_{5}} = 0.74136507 * 0.186815602 * 0.593269992 = 0.082167041$

この計算をデルタルールという形で組み合わせているのをよく見かけます。

$\frac{partial E_{total}}{\ w_{5}} = -(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1}) * out_{h1}$

別の方法としては。となり、 $\frac{˶E_{total}}{˶out_{o1}}$ $〘frac{˶E_{o1}}{˶out_{o1}〙となります。 out_{o1}}{\\ net_{o1}}$ $\frac{\ E_{total}}{\ net_{o1}}$ $\delta_{o1}$ （ギリシャ文字のデルタ）、別名、ノードデルタです。

$delta_{o1} = ˶ˆ꒳ˆ˵ )$

$delta_{o1}$ (ギリシャ文字のデルタ、別名ノードデルタ)を使って、上の計算を書き換えることができます。

$Delta_{o1} = - (target_{o1} - net_{o1})(target_{o1} - out_{o1}) * out_{o1}(1 - out_{o1})$

従って、以下のようになります。

$\frac{partial E_{total}}{\ w_{5}} = \delta_{o1} out_{h1}$

$delta$ から負の符号を抽出して、次のように書く資料もあります。

$\frac{partial E_{total}}{partial w_{5}} = -delta_{o1} out_{h1}$

誤差を減らすために、現在の重みからこの値を差し引きます（任意で学習率 eta を掛けますが、ここでは 0.5):

$w_5^{+} = w_5 - eta * \frac{\partial E_{total}}{\partial w_{5}} = 0.4 - 0.5 * 0.082167041 = 0.35891648$

学習率を表すのに、 $\alpha$ $\eta$ $\epsilon$ （イプシロン）を使う資料もあります。

この作業を繰り返して、 $w_6$ $w_7$ $w_8$ という新しい重みを得ることができます：

$w_6^{+} = 0.408666186$

$w_7^{+} = 0.511301270$

$w_8^{+} = 0.561370121$

隠れ層のニューロンにつながる新しい重みを得た後、ニューラルネットワークで実際の更新を実行します (つまり、以下のバックプロパゲーションアルゴリズムを続行する際には、更新された重みではなく、元の重みを使用します)。

隠れ層

次に、 $w_1$ $w_2$ $w_3$ $w_4$ の新しい値を計算します。

全体像を把握するには、次のようにします。

$\\\ w_{1} = ˶ˆ꒳ˆ˵ ) * ˶ˆ꒳ˆ˵ )$

視覚的に。

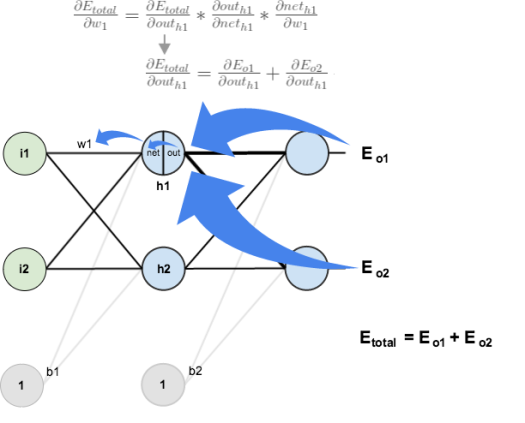
nn-calculation

出力層で行ったのと同様のプロセスを使用しますが、各隠れ層ニューロンの出力が複数の出力ニューロンの出力 (したがって誤差) に寄与するという事実を考慮して、若干異なります。 $out_{h1}$ $out_{o1}$ $out_{o2}$ の両方に影響を与えることが分かっています。

$\frac{partial E_{total}}{̫⃝{out_{h1}}$ は、両方の出力ニューロンへの影響を考慮する必要があります。

$\frac{partial E_{total}}{\frac{out_{h1}} = ˶‾᷄덴덴 E_{o1}}{\frac{out_{h1}}$

まず、 $\frac{\partial E_{o1}}{\partial out_{h1}}$ から始めます。

$\frac{˶E_{o1}}{˶E_{h1}} = ˶E_{o1}}{˶E_{o1}} net_{o1}}$

先ほど計算した値を使って、 $\\ E_{o1}}{\ net_{o1}}$ を計算することができます。

$\frac{\partial E_{o1}}{\partial net_{o1}} = ˶ˆ꒳ˆ˵ ) * 0.74136507 * 0.186815602 = 0.138498562$

そして、 $\frac{parttial net_{o1}}{parttial out_{h1}}$ $w_5$ と等しくなります：

$net_{o1} = w_5 * out_{h1}. + w_6 * out_{h2} + b_2 * 1$

$\frac{partial net_{o1}}{\partial out_{h1}} = w_5 = 0.40$

プラグイン：

$\frac{partial E_{o1}}{partial out_{h1}} = ˶‾᷄덴덴{o1}}{partial net_{o1}} * 0.138498562 * 0.40 = 0.055399425$

$\frac{\partial E_{o2}}{\partial out_{h1}}$ についても同様に考えると、次のようになります。019049119

Therefore:

$\frac{partial E_{total}}{\frac{out_{h1}} = ˶ˆ꒳ˆ˵ ) + ˶ˆ꒳ˆ˵ ) = 0.055399425 + -0.019049119 = 0.036350306$

さて、 $\frac{partial E_{total}}{\frac{out_{h1}}$ が得られました。

$frac{partial E_{total}}{}{partial out_{h1}}$ $frac{partial net_{h1}}{˶w}$ を計算する必要があります。

$out_{h1} = ″frac{1}{1+e^{-net_{h1}}″$

$\frac{partial out_{h1}}{partial net_{h1}} = out_{h1}(1 - out_{h1}) = 0.59326999(1 - 0.59326999 ) = 0.241300709$

出力ニューロンで行ったのと同じように、 $h_1$ $w_1$ に対する偏微分を計算します。

$net_{h1} = w_1 * i_1 + w_3 * i_2 + b_1 * 1$

$frac{˶ˆ꒳ˆ˵ net_{h1}}{˶ˆ꒳ˆ˵ w_1} = i_1 = 0.05$

Putting all is it together:

$˶‾᷅˵‾᷄˵ E_{total}}{˶‾᷄˵ E_{total}}{˶‾᷄˵ E_{total}}{˶‾᷄˵ E_{h1} = ˶‾᷄˵ E_{total}}{˶‾᷅˵ E_{h1} * ˶‾᷄˵ E_{total}}{˶‾᷅˵ * ˶ˆ꒳ˆ˵ ) * ˶ˆ꒳ˆ˵ )$

$˶ˆ꒳ˆ˵ )$

= 0.036350306 * 0.241300709 * 0.05 = 0.000438568

これを次のように書くこともできます。

$\frac{\partial E_{total}}{\partial w_{1}} = (sums\limits_{o}{\frac{\partial E_{total}}{\partial out_{o}}) * ˶ˆ꒳ˆ˵ ) * ˶ˆ꒳ˆ˵ ) * ˶ˆ꒳ˆ˵ ) * ˶ˆ꒳ˆ˵ )$

$˶ˆ꒳ˆ˵ )$

= (˶ˆ꒳ˆ˵ ) out_{h1}) * i_{1}

$\frac{partial E_{total}}{\partial w_{1}} = ˶ˆ꒳ˆ˵ )$

これで $w_1$ を更新することができました。

$w_1^{+} = w_1 - ˶ˆ꒳ˆ˵ * ˶ˆ꒳ˆ˵ }}{˶ˆ꒳ˆ˵ w_{1}} = 0.15 - 0.5 * 0.000438568 = 0.149780716$

これを $w_2$ $w_3$ $w_4$

$w_2^{+} = 0.19956143$

$w_3^{+} = 0.24975114$

$w_4^{+} = 0.29950229$

最終的に、すべてのウェイトを更新しました! 最初に 0.05 と 0.1 の入力をフィードフォワードしたとき、ネットワークのエラーは 0.298371109 でした。今回のバックプロパゲーションの結果、誤差の合計は0.291027924となりました。しかし、これを例えば1万回繰り返すと、誤差は0.0000351085にまで減少します。

ここまで来て、上記のいずれかに誤りを発見したり、将来の読者のためにもっとわかりやすくする方法を思いついたりしたら、遠慮なく私に連絡してください。ありがとうございました！