このチュートリアルでは、Active Band Pass Filterについて、その周波数特性、タイプ、例などを学びます。
バンドパスフィルタは、他のフィルタと同様に、トランジスタやオペアンプなどのアクティブなコンポーネントで設計することができます。
概要
はじめに
バンドパスフィルターとは、特定の帯域の周波数のみを通過させる回路です。 この通過帯域は主にカットオフ周波数の間にあり、それらはfLとfHです。
中心周波数は「fC」で示され、共振周波数やピーク周波数とも呼ばれます。
fLの値は常にfHの値よりも小さくなければなりません。 フィルターの通過帯域は、帯域幅に他なりません。 フィルターの利得は、共振周波数または中心周波数で最大となり、これを全通過帯域利得と呼びます。
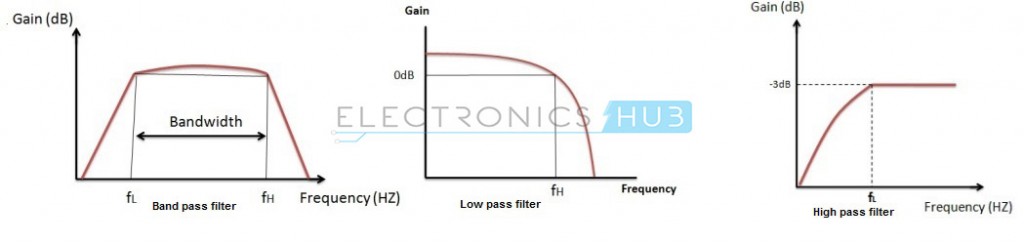
ローパスフィルターの場合、このパスバンドは0Hzから始まり、最大パスバンドゲインから-3dB下がったところで共振周波数の値に達するまで続きます。
ハイパス・フィルターの場合、このパスバンドは、-3 dBの共振周波数から始まり、アクティブ・フィルターの最大ループ・ゲインの値で終わります。 ローパス応答とハイパス応答の組み合わせにより、以下のようなバンドパス応答が得られます:
BACK TO TOP
アクティブバンドパスフィルタ
品質係数によって、バンドパスフィルタはワイドバンドパスフィルタとナローバンドパスフィルタに分類されます。 品質係数は「メリットの数値」とも呼ばれています。

これらのハイパスフィルタとローパスフィルタの間の増幅回路は、アイソレーションを提供し、回路のオーバーオール電圧ゲインを与えます。 両フィルターのカットオフ周波数の値は、最小の差で維持されなければなりません。
この差が非常に小さい場合、ハイパスとローパスのステージが相互に影響し合う可能性があります。
アクティブバンドパスフィルターの回路図を以下に示します。アクティブバンドパスフィルタの回路図
BACK TO TOP
ワイドバンドパスフィルタ
Quality Factorの値が10以下であれば、通過帯域が広くなり、より広い帯域を得ることができます。
このフィルタでは、高いカットオフ周波数が低いカットオフ周波数よりも大きくなければなりません。 設計には2つの増幅素子(オペアンプ)を使用しています。
まず、信号はハイパス・フィルタを通過し、このハイパス・フィルタの出力信号は無限大に傾くので、無限大に傾いた信号は最後にローパス・フィルタに与えられます。
このローパス・フィルタは高周波信号を低域通過させます。
ハイパス・フィルタをローパス・フィルタとカスケード接続すると、単純なバンドパス・フィルタが得られます。 このフィルターを実現するためには、ローパス回路とハイパス回路の順序を同じにする必要があります。
1つの1次のローパスとハイパスをカスケード接続すると、2次のバンドパス フィルターが得られ、2つの1次のローパス フィルターと2つのハイパス フィルターをカスケード接続すると、4次のバンドパス フィルターが得られます。
このカスケード接続により、回路は低い値の品質係数を生成します。
2次フィルター(High + Low)の場合、両方のストップバンドでのゲインロールオフは±20 dB/decadeです。
同様に、ハイパスフィルタとローパスフィルタが2次の場合、両方のストップバンドでのゲインロールオフは±40dB/decadeとなります。
バンドパスフィルタの電圧利得の式は次のように与えられます:
| Vout / Vin | = / √{}
それはハイパスフィルタとローパスフィルタの両方の個別の利得によって得られ、ハイパスフィルタとローパスフィルタの両方の個別の利得は次のように与えられます。
ハイパスフィルターの電圧利得:
| Vout / Vin | = / √
ローパスフィルターの電圧利得。
| Vout / Vin | = Amax2 / √
Amax = Amax1 * Amax2
ここで、Amaxx1はハイパス段のゲイン、Amaxx2はローパス段のゲインです。
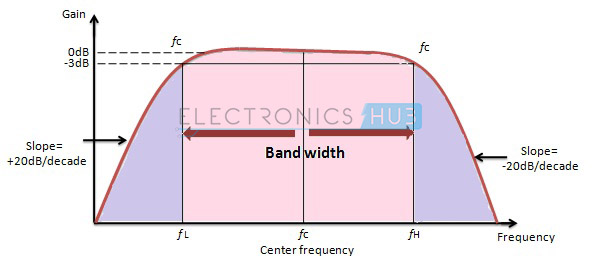
広帯域フィルタの応答を以下に示します。
BACK TO TOP
狭帯域フィルタ
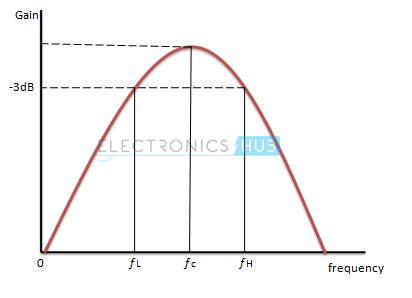
品質係数の値が10より大きい場合、通過帯域は狭くなり、帯域幅も狭くなります。
能動素子(オペアンプ)を2つではなく1つだけ使用し、このオペアンプを反転構成にしたバンドパスフィルタをNarrow Band Pass Filterと呼びます。
BACK TO TOP
狭帯域通過フィルタの回路
入力を反転入力端子に印加します。 これは、オペアンプが反転構成であることを示しています。


上記のフィルタ回路の電圧利得は、AV = – R2 / R1
フィルタ回路のカットオフ周波数は、
R1 / R2 / R3
R2 / R3 p
fC1 = 1 / (2πR1C1)、fC2 = 1 / (2πR2C2)
BACK TO TOP
Multi Feedback Active Band Pass Filter
このフィルター回路は、フィルターの負のフィードバックに基づいて、同調回路を生成します。 この多重帰還の重要な利点は、中心周波数での最大利得を変えることなく、カットオフ周波数の値を変えることができることです。 このカットオフ周波数の変更は、抵抗「R3」によって行うことができます。
以下のアクティブフィルター回路を考え、変更された抵抗値をR3′、変更されたカットオフ周波数の値をfc′とすると、新しい抵抗値は以下のように計算できます:
R3′ = R3(fc /fc′)²
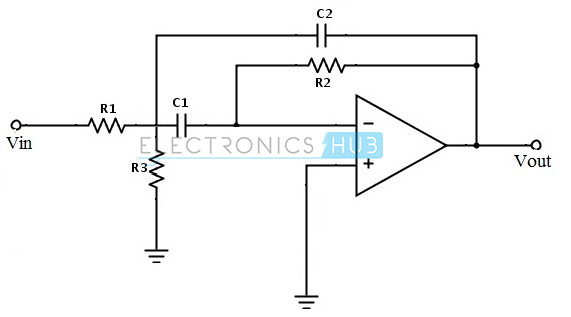
2つのフィードバック・パスから構成されており、この複数のフィードバック・パスから、「マルチ・フィードバック・バンドパス回路」とも呼ばれます。 この回路は、無限ゲインの多重帰還バンドパスフィルタを生成します。 この回路により、品質係数の値は最大で20まで上昇します。
fc = 1/√(R1R2C1C2)
Q = fc/Bandwidth = (1/2){√}
Amax = -.R2/2R1
R1 = Q/{2πfcCAmax}
R2 = Q/πfcC
R3 = Q/{2πfcC(2Q² – Amax)}
中心周波数「Amax」での利得は2Q²より小さくなければなりません。 つまり、
Amax < 2Q²
ここで、
fc = カットオフ周波数(Hz)
C = 静電容量。 (C1 = C2 = C)
Q = 品質係数
Amax = 最大利得
BACK TO TOP
アクティブバンドフィルターの周波数特性
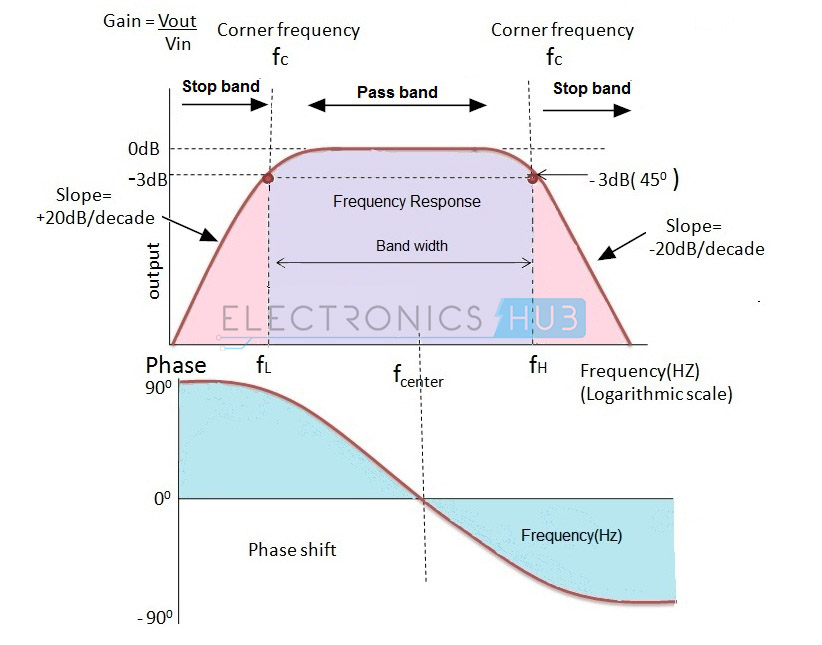
ハイパスフィルターとローパスフィルターの2つの中心周波数を持っています。 ハイパスフィルタの中心周波数は、ローパスフィルタの中心周波数よりも低くなければなりません。
バンドパスフィルタの中心周波数は、ローカットオフ周波数とアッパーカットオフ周波数の幾何学的平均値fr2 = fH * fLです。
フィルターのゲインは20 log (Vout/Vin) dB/Decadeです。 振幅応答は、ローパスフィルタとハイパスフィルタの応答と同様です。
正規化された中間周波数はfr = 1として与えられます。
BACK TO TOP
品質係数
品質係数は、通過帯域の帯域幅に依存します。 品質係数は帯域幅に反比例します。
Q = fc/Bandwidth
広帯域のパスフィルターでは、パスバンドの幅が大きいため、品質係数は低くなります。 狭帯域のパスフィルターでは、品質係数は高い。
この品質係数は、ダンピング係数()とも関係があります。
この品質係数は、ダンピング係数()にも関係しており、ダンピング係数の値が大きければ、出力レスポンスのフラットさも大きくなります。
ε=2/Q
異なる品質係数の値に対して、2次バンドパスフィルタの正規化された利得応答は次のように与えられます:
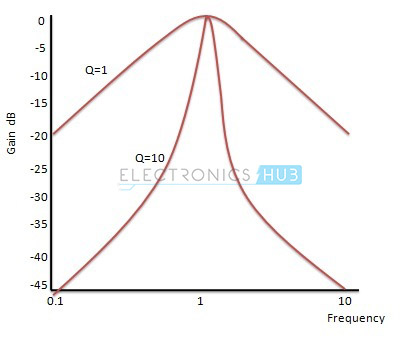

このグラフから、品質係数が高いほど選択性が高くなることがわかります。
BACK TO TOP
アクティブバンドパスフィルタの例
無限ゲインの多重帰還アクティブフィルタ回路を考えてみましょう。
抵抗について
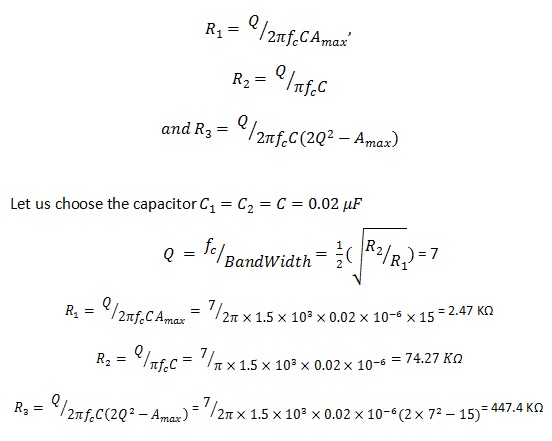
変更された抵抗値をR3´、変更されたカットオフ周波数をfc´=2KHzとすると、新しい抵抗値は次のように計算できます。