قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). Brug’s law (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).

定義

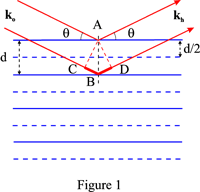
ブラッグの法則は、平面波が格子面のファミリーによって回折されるための条件を提供しています。

2 d sin θ = n λ

ここでdは平面間の間隔、θは入射平面波の波動ベクトルkoと格子面の間の角度、λはその波長、nは反射の次数である整数です。

ブラッグの法則の直接導出

• 第一面からの反射

反射波のベクトルの角度khがθにも等しい場合、第一面の点状散乱体の分布がどうであれ、散乱波は位相が揃う。これがSnell-Descartesの反射の法則である。

• 第2面からの反射

反射波の位相は面内の点散乱体の位置に依存しないので、連続する2つの格子面で反射される波の位相差は、第1面上の散乱点Aと第2面上の散乱点BをABが面の法線になるように任意に選ぶことで得られる。 Bを通る入射波と反射波のベクトルにAを投影したものをCとDとすると、AとBでそれぞれ反射した波の経路差は、図1から明らかです。

CB + BD = 2d sin θ

そして、この経路差がnλ（nは整数）に等しければ、2つの波は位相が揃うことになります。

• 第3などの面からの反射

最初の2つの面でブラッグの関係が満たされていれば、波動ベクトルkhで反射した波は、ファミリーのすべての面で位相が揃うことになります。

反射の次数

ブラッグの法則は次のように書くこともできます：

2 (d/n) sin θ = λ.

そうすると、次数nの格子面ファミリー上での次数nのブラッグ反射は、架空の、または想像上の格子間隔の平面ファミリー上での次数1の反射と同等であると言うことができます

d_{hkl} = d/n.

この架空のファミリーは、OH = n/d = 1/d_{hkl}となる逆格子ベクトルOHと関連しています。 反射の指標はhklです。 例えば、図1の破線の水平線は、2次、n = 2に関連する架空の平面に対応しています。

反射条件

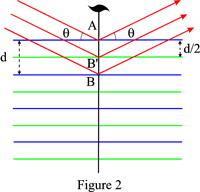
格子面に垂直なグライド面またはねじ軸がある場合、実際の反射面の間隔は、グライド面の場合はd/2、ねじ軸がqpの場合は(d p/q)となります。 そして、ブラッグの法則は次のように書かれるはずです。

2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ

グライド面の場合と

iv

2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ

ねじ軸qpの場合。

グライドプレーンでは奇数次、スクリュー軸では(q/p)nと異なる次数の反射がありません。

例として、図2は21本のねじ軸の場合を示しています。反射面は青の面と、ねじ軸の作用によって後者から推測される緑の面です。

変形の影響

ある格子面群(hkl)が歪まず、その格子間隔dが変わらない変形は、kkl反射のブラッグ角に影響を与えません。

歴史

Bragg (1890-1971)は、1912年11月11日にCambridge Philosophical Societyのミーティングで、反射条件の導出を発表しました。 彼の論文は1913年に出版されました。 詳細は、P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Section 5, p.64およびA. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Section 6.11, p.120を参照してください。