クロス集計表のカイ二乗統計量の計算

カイ二乗統計量は、まず表の各セルのカイ二乗値を計算し、次にそれらを合計して表の合計カイ二乗値を形成することによって計算されます。 セルのカイ二乗値は次のように計算されます。 (観測値-期待値)2 / (期待値)。

この表の例では、表のカイ二乗値が19.35であり、1000回に1回以下の確率で偶然に発生することがわかります。 したがって、差がないという帰無仮説を棄却し、変数間には関係があるはずだと結論づけます。

最も明らかなのは、各セルに計算されたカイ二乗値です。 レッドソックスとボストン」、「ブルージェイズとモントリオール」、「レッドソックスとバーモント州モンペリエ」の3つのセルでは、観測された回答者の数が予想よりも多かったことがわかります。 さらに、期待値と観測値の頻度を調べると、「ヤンキースとモントリオール」、「レッドソックスとバーモント州モンペリエ」、「レッドソックスとモントリオール」の頻度が期待値よりも少なかったことに注目します。

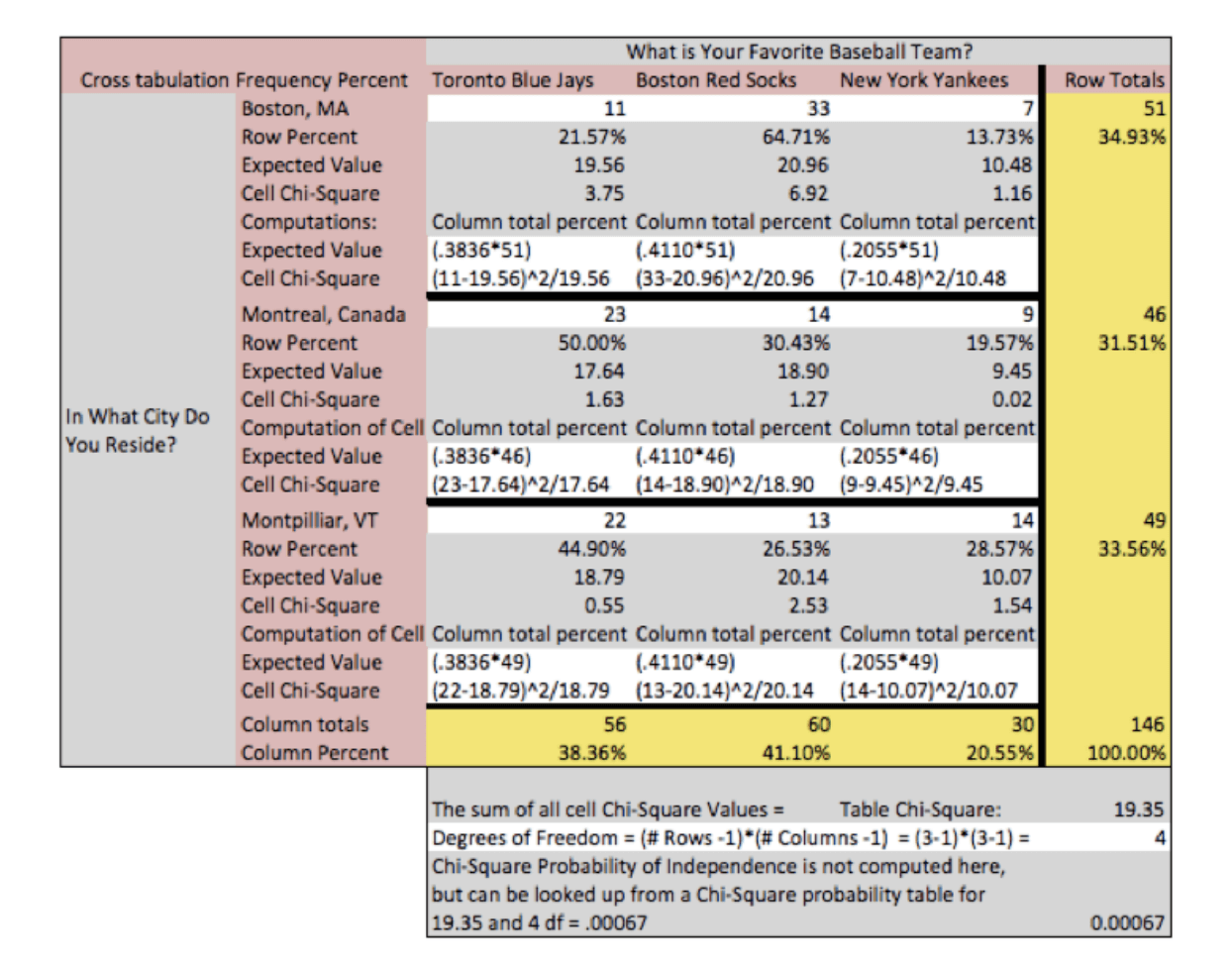
セルのカイ二乗と期待値は表示されないことが多いため、列合計のパーセントとセルのパーセント (行合計の) を比較することで、これらの同じ関係を観察することができます。 セル「レッドソックスとボストン」では、41.10%と64.71%を比較し、レッドソックスのファンのうち、ボストンが好きな人が予想よりも多いことがわかります。 統計解析で得られた関係を解釈する際には、注意が必要です。

現在の表では、「レッドソックスとボストン」は、どのチームの好みでも、居住都市でも、観察された回答者数と予想された回答者数の間のデルタが最大であることがわかります。 しかし、レッドソックスが回答者をボストンに移動させたとか、居住都市としてのボストンがファンの忠誠心を高めたと結論づけるのは、慎重にしなければなりません。 レッドソックスとボストンは、最も観察されたファンと都市の関係ですが、他の概念や関係を考慮すると、完全に独立している可能性が高いのです。

クロスタブやカイ二乗は、調査データを分析する強力な方法です。また、調査に影響を与える人気のあるツールとして、コンジョイント分析があります。