背景
楕円曲線暗号(Elliptic Curve Cryptography: ECC)は、有限体上の楕円曲線の代数的な構造に基づいた公開鍵暗号のアプローチです。
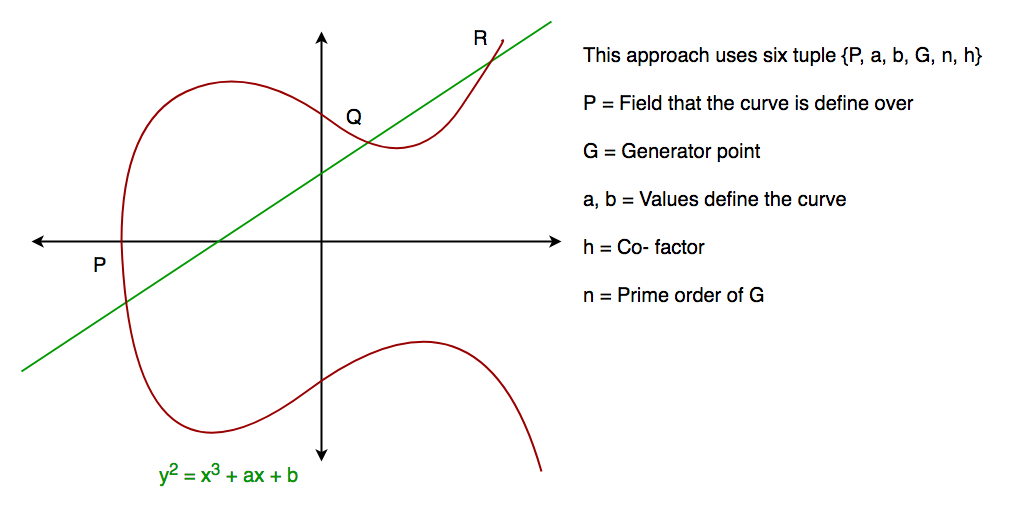
楕円曲線暗号の理解を深めるためには、楕円曲線の基本を理解することが非常に重要です。 楕円曲線とは、平面的な代数曲線で、次のような式で定義されます。
その曲線は非特異点であり、そのグラフには尖った部分や自己交差部分がありません。
一般的に、楕円曲線は以下のような形をしています。 楕円曲線は、曲線と交差する直線を引くと、ほぼ3点で交差します。 楕円曲線はx軸を中心に対称であることがわかりますが、この性質はアルゴリズムにおいて重要な役割を果たします。
Diffie-Hellmanアルゴリズム
Diffie-Hellmanアルゴリズムは、楕円曲線を使って点を生成し、そのパラメータを使って秘密鍵を得ることで、公衆ネットワーク上でデータを交換しながら、秘密通信に使用できる共有秘密を確立するために使用されています。
- アルゴリズムを簡単にして実用的にするために、1つの素数PとG(Pの原始根)、2つの秘密値aとbの4つの変数だけを考えます。
- PとGはどちらも公開されている数字です。
- PとGはどちらも公開されている数字です。ユーザー(AliceとBobとします)が秘密値aとbを選び、鍵を生成して公開で交換し、反対側の人はその鍵を受け取り、そこから秘密鍵を生成し、その後、同じ秘密鍵で暗号化します。
Step by Step Explanation
| Alice | Bob |
|---|---|
| パブリック・キーあり=P, G | Public Keys available = P, G |
| Private Key Selected = a | Private Key Selected = b |
| Key generated!
|
生成されたキー =
|
| 生成されたキーの交換が行われる | |
| キー 受信したキー=y | 受信したキー=x |
|
生成されたシークレットキー =
|
|
|
代数的には次のように示すことができます
。 |
|
| ユーザーは暗号化するための対称的な秘密鍵を持つことになります | |
例
Step 1: Alice and Bob get public numbers P = 23, G = 9Step 2: Alice selected a private key a = 4 and Bob selected a private key b = 3Step 3: Alice and Bob compute public valuesAlice: x =(9^4 mod 23) = (6561 mod 23) = 6 Bob: y = (9^3 mod 23) = (729 mod 23) = 16Step 4: Alice and Bob exchange public numbersStep 5: Alice receives public key y =16 and Bob receives public key x = 6Step 6: Alice and Bob compute symmetric keys Alice: ka = y^a mod p = 65536 mod 23 = 9 Bob: kb = x^b mod p = 216 mod 23 = 9Step 7: 9 is the shared secret.
実装してみました。
#include<stdio.h>#include<math.h>longlongintpower(longlonginta, longlongintb, longlongintP) { if(b == 1) returna; else return(((longlongint)pow(a, b)) % P); }intmain() { longlongintP, G, x, a, y, b, ka, kb; P = 23; printf("The value of P : %lld\n", P); G = 9; printf("The value of G : %lld\n\n", G); a = 4; printf("The private key a for Alice : %lld\n", a); x = power(G, a, P); div
b = 3; printf("The private key b for Bob : %lld\n\n", b); y = power(G, b, P); ka = power(y, a, P); div
kb = power(x, b, P); printf("Secret key for the Alice is : %lld\n", ka); printf("Secret Key for the Bob is : %lld\n", kb); return0; }
fromrandom importrandint if__name__ =='__main__': div P =23 div G =9 print('The Value of P is :%d'%(P)) print('The Value of G is :%d'%(G)) a =4 div
print('The Private Key a for Alice is :%d'%(a)) x =int(pow(G,a,P)) b =3 print('The Private Key b for Bob is :%d'%(b)) y =int(pow(G,b,P)) ka =int(pow(y,a,P)) div
kb =int(pow(x,b,P)) print('Secret key for the Alice is : %d'%(ka)) print('Secret Key for the Bob is : %d'%(kb)) iv
アウトプット
The value of P : 23The value of G : 9The private key a for Alice : 4The private key b for Bob : 3Secret key for the Alice is : 9Secret Key for the Bob is : 9
この記事はSouvik Nandi氏からの寄稿です。 もしあなたがGeeksforGeeksを気に入ってくださり、貢献したいと思ってくださったなら、contribute.GeeksforGeeks.orgを使って記事を書いていただくか、 [email protected] までメールでお送りください。 あなたの記事がGeeksforGeeksのメインページに掲載されるのを見て、他のGeeksを助けてください。
間違っている点を見つけたり、上記のトピックについてもっと情報を共有したい場合は、コメントを書いてください。
div