これはベクトルです:

ベクトルには大きさ(サイズ)と方向があります。
線の長さはその大きさを示し、矢じりは方向を指しています。
2つのベクトルを頭から尻尾までつなげて足すことができます:
しかも、どの順番で足しても同じ結果になります。
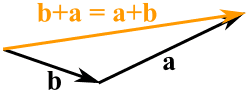
例を挙げます。
2つのベクトル(プロペラによる速度と風の速度)により、北から少し東に向かう地上速度が少し遅くなります。
地上から飛行機を見ると、少し横にずれているように見えるでしょう。
そんなことを見たことはありませんか? もしかしたら、強風に苦戦している鳥が横向きに飛んでいるように見えるのを見たことがあるかもしれません。
速度、加速度、力など、さまざまなものがベクトルです。
引き算
あるベクトルから別のベクトルを引くこともできます。
- まず、引きたいベクトルの向きを逆にします。
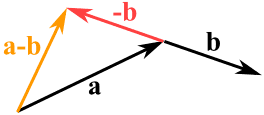
a – b
注釈
ベクトルはaやbのように太字で書かれることが多いです。
| ベクトルは次のように、頭と尻尾の文字 に上に矢印をつけて書くこともできます。 |
Calculations
さて.……どうやって計算するのでしょうか?
最も一般的な方法は、以下のように、まずベクトルをxとyの部分に分割することです:
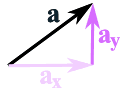
ベクトルaは、
2つのベクトルaxとayに分割されます
(この方法は後述します。
ベクトルの足し算
xの部分を足し算し、yの部分を足し算してベクトルを足すことができます:
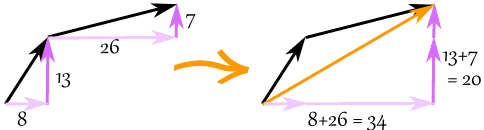
ベクトル(8, 13)とベクトル(26, 7)を足し算して、ベクトル(34, 20)になります
例: ベクトルa = (8, 13)とb = (26, 7)を足す
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
このようにベクトルを分解するとき、それぞれの部分を成分といいます。
ベクトルの引き算
引き算をするには、まず引きたいベクトルを反転させ、次に足し算をします。
例を示します。 v = (12, 2)からk = (4, 5)を引く
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
ベクトルの大きさ
ベクトルの大きさは、ベクトルの両脇にある2本の縦棒で示されます。
|a|
または、(絶対値と混同しないように)二重の縦棒で書くこともできます。
|a||
ピタゴラスの定理を使って計算します:
|a| = √( x2 + y2 )
例題:ベクトルb = (6, 8)の大きさは何ですか?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
大きさが1のベクトルを単位ベクトルといいます。
ベクトルとスカラーの比較
スカラーは大きさ(サイズ)のみを持ちます。
- だからcはベクトルで、大きさと方向を持っています
- でもcは3や12のようにただの値です
- だからcはベクトルで、大きさと方向を持っています
- でもcは3や12のようにただの値です。4
- スカラーまたはドット積(結果はスカラー)
- ベクトルまたはクロス積(結果はベクトル)
- x = r × cos( θ )
- y = r × sin( θ )
- r = √ ( x2 + y2 )
- θ = tan- 。1 ( y / x )
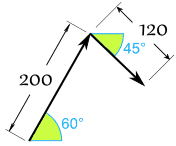
- サムは60°で200ニュートンの力で引っ張ります
- アレックスは図のように45°で120ニュートンの力で引っ張ります
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84.85
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88.36 / 184.85 ) = 25.5°
例:kbは実際にはスカラーkにベクトルbを掛けたものです。
Multiplying a Vector by a Scalar
ベクトルにスカラーを掛けることは、ベクトルの大きさや小ささを変えることになるので、「スケーリング」と呼ばれます。
例を示します。 ベクトルm=(7, 3)にスカラー3を乗じる
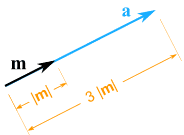 |
a = 3m = (3×7, 3×3) = (21, 9) |
まだ同じ方向を向いていますが、3倍長くなっています
(そして、なぜ数が「スカラー」と呼ばれるのか、それはベクトルを上下に「スケーリング」するからだということがわかりました。)
ベクトルとベクトルの掛け算(ドット積とクロス積)
 |
2つのベクトルを掛け合わせるにはどうすればよいのでしょうか? (詳細はこれらのページをお読みください。) |
2次元以上
ベクトルは3次元以上でも完全に動作します。
ベクトル (1, 4, 5)
Example: ベクトルa = (3, 7, 4)とb = (2, 9, 11)を足す
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
例:ベクトルw = (1, -2, 3)の大きさは何ですか?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9 ) = √14
ここで、4次元の例を挙げます(ただし、描くのは難しい!)。):
例です。 (3, 3, 3, 3)から(1, 2, 3, 4)を引く
(3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3) + (-1, -2, -3, -4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
大きさと方向
ベクトルの大きさと方向はわかっていても、xとyの長さ(またはその逆)が知りたい場合があります。
 |
<> |  |
| 極座標におけるベクトルa | デカルトにおけるベクトル |
極座標と直交座標での変換方法をご覧ください。
変換方法は極座標と直交座標でご覧いただけますが、ここでは簡単にまとめてみました。
| 極座標(r,θ) から直交座標(x,y)へ |
直交座標(x,y) から極座標(r,θ) |
|
|---|---|---|
|
|
|
An example
SamとAlexが箱を引っ張っています。
結合された力とその方向は何でしょうか?
2つのベクトルを頭から尻尾まで加えてみましょう:
まず極座標からデカルト座標への変換(小数点以下2桁まで):
サムのベクトル:
Alexのベクトル:
これで次のようになりました:
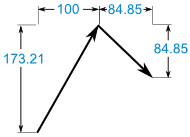
足し算:
(100, 173.21) + (84.85, -84.85) = (184.85, 88.36)
この答えは有効ですが、質問が極座標だったので極座標に変換してみましょう:
そして、次のような(丸められた)結果が得られました: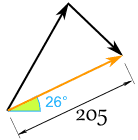
そして、サムとアレックスの場合は次のようになります:
肩を並べていれば、もっと良い結果が得られるかもしれません!
このような結果が得られました。






