Posted on 1st October 2018 by Eveliina Ilola

交絡とは、第三の変数が両方と独立して関連しているために、独立変数と従属変数の間の関連性が歪められることを意味します。
2つの変数の間の因果関係は、独立変数が従属変数に影響を与える方法としてよく説明されます。 独立変数は独立して異なる値を取ることができ、従属変数は独立変数の値に応じて変化します。
例えば、アルコールの消費量が死亡率にどのような影響を与えるかを調べたいとします。
あなたは、アルコールのヘビーユーザーと禁酒家からなる2つのグループの死亡率を比較することにしました。
アルコールの消費量が多い人ほど死亡する確率が高いことがわかった場合、アルコールの使用が死亡のリスクを高めると直感的に結論づけることができるかもしれません。 しかし、実際には、状況はもっと複雑かもしれません。
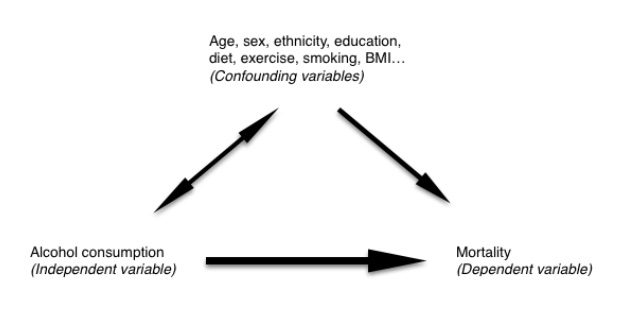
アルコール摂取量が少ない人は、健康的な食生活を送っていたり、喫煙率が低かったりする可能性があります。
例えば、アルコール摂取量が少ない人は、健康的な食事をしている可能性が高く、喫煙率も低いかもしれません。 このような他の影響因子を交絡変数と呼びます。 これらを無視して、死亡率の差がアルコール摂取量の差によって引き起こされるに違いないと仮定すると、現実をあまり反映していない結果になってしまう可能性があります。
研究デザインで交絡の影響を最小限に抑える方法
介入の効果を調査する場合、介入群と対照群に無作為に人々を割り当てることができます。 無作為化の目的は、既知の交絡因子と未知の交絡因子を2つのグループに均等に配分することです。 偶然、両群間に潜在的な交絡因子の差が生じることがありますが、無作為化によりその差を最小限に抑えることができます。
他のタイプの研究では、制限やマッチングによって交絡に対処することができます。 制限とは、交絡変数の点で類似している人のみを対象とすることです。例えば、年齢が交絡変数であると考えた場合、65歳以上の人のみを対象とすることができます。 例えば、年齢が交絡変数であると考えた場合、65歳以上の人だけを対象とすることができます。 マッチングとは、潜在的な交絡因子に基づいて、2つのグループの人々をペアにすることです。
統計解析中に交絡の影響を最小限に抑える方法
研究を終えた後、統計的手法を用いて交絡の影響を最小限に抑えることができます。 層別では、交絡変数が変化しない小さなグループを作り、それぞれのグループで独立変数と従属変数の関係を調べます。
潜在的な交絡因子の数が多ければ、ロジスティック回帰や線形回帰などの多変量解析を使用することができます。
結論
2つの変数の間の関連性は、第3の変数によって修正される可能性があり、これによって結果が歪められる可能性があります。 しかし、その影響を減らすための最初のステップは、結果を歪める可能性があることを認識し、それに応じて計画を立てることです。
Pourhoseingholi, M. A., Baghestani, A. R., & Vahedi, M. (2012). 統計解析で交絡効果をコントロールする方法。 Gastroenterology and Hepatology From Bed to Bench, 5(2), 79-83.
Catalogue of bias collaboration, Aronson JK, Bankhead C, Nunan D. Confounding. In Catalogue Of Biases. 2018. https://catalogofbias.org/biases/confounding/
http://www.ucl.ac.uk/ich/short-courses-events/about-stats-courses/stats-rm/chapter_1_content/Confounding_Factors