p>taxas de Erro Familiar > Holm-Método Bonferroni

p>P>Pode querer ler primeiro este artigo: Taxas de erro familiares.

Qual é o Método Holm-Bonferroni?

O Método Holm-Bonferroni (também chamado Procedimento Sequencial de Holm Bonferroni) é uma forma de lidar com as taxas de erro familiares (FWER) para múltiplos testes de hipóteses. É uma modificação da correcção de Bonferroni. A correcção Bonferroni reduz a possibilidade de obter um resultado estatisticamente significativo (ou seja, um erro de Tipo I) ao realizar múltiplos testes. Embora o Bonferroni seja simples de calcular, sofre de uma falta de poder estatístico. O método de Holm-Bonferroni é também bastante simples de calcular, mas é mais poderoso que o método de um único passo Bonferroni.

Fórmula

A fórmula para calcular o Holm-Bonferroni é: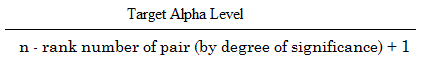

onde:

ul>

Este próximo exemplo mostra como funciona a fórmula.

Exemplo

Question: Usar o método Holm-Bonferroni para testar as quatro hipóteses seguintes e os seus valores p associados a um nível alfa de .05:

• H1 = 0.01.
• H2 = 0.04
• H3 = 0.03
• H4 = 0.005

Nota: já sabemos os valores p associados a cada hipótese. Se não souber os valores p, faça um teste para cada hipótese antes de tentar ajustar o FWER usando o método Holm-Bonferroni.

P>Passo 1: Encomende os valores p do mais pequeno para o maior:

• H4 = 0.005
• H1 = 0.01
• H3 = 0.03
• H2 = 0.04

Step 2: Trabalhar a fórmula de Holm-Bonferroni para a primeira posição:
HB = Alvo α / (n – posição + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

P>Passo 3: Compare o valor p do primeiro grau (menor) do Passo 1 com o nível alfa calculado no Passo 2:
Valor p mais baixo, no Passo 1 (H4 = 0.005) <Nível alfa, no Etapa 2 (.0125).
Se o valor de p for menor, rejeitar a hipótese nula para este teste individual.

O valor p de .005 é inferior a .0125, pelo que a hipótese nula para H4 é rejeitada.

P>Passo 4: Repetir a fórmula HB para o segundo nível.
HB = Alvo α / (n – classificação + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

P>Passo 5: Comparar o resultado da fórmula HB no Passo 4 com o valor p do segundo classificado:
Segundo valor p, no Passo 1 (H1 = 0,01) < Nível Alfa no Passo 2 (.0167).
O valor p de .01 é inferior a .0167, pelo que a hipótese nula para H1 também é rejeitada.

passo 6: Repetir a fórmula HB para o terceiro nível.
HB = Alvo α / (n – nível + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

passo 7: Comparar o resultado da fórmula HB no passo 6 com o valor p do terceiro nível:
Terceiro valor de p, no Passo 1 (H3 = 0.03) >Nível Alfa no Passo 6 (.025).
O valor de p de .03 é superior a .025, pelo que a hipótese nula para H3 não é rejeitada.

Os testes param quando se atinge a primeira hipótese não rejeitada. Todas as hipóteses subsequentes são não significativas (ou seja, não rejeitadas).

Referência:
Holm, S. 1979. Um procedimento de teste múltiplo simples e sequencialmente rejeitado. Scandinavian Journal of Statistics 6:65-70

——————————————————————————
p>Need help with a homework or test question? Com o Chegg Study, pode obter soluções passo a passo para as suas perguntas de um especialista na matéria. Os seus primeiros 30 minutos com um tutor de Chegg são gratuitos!