In deze tutorial leren we over actieve banddoorlaatfilters, hun frequentierespons, types, voorbeelden en nog veel meer. In een eerdere tutorial hebben we gezien over Band Pass filters, maar de ontwerpbenadering in die tutorial was gebaseerd op passieve componenten.
Band Pass Filter, net als elk ander filter, kan worden ontworpen rond actieve componenten zoals Transistors en Op-amps. Als je meer informatie wilt over passieve banddoorlaatfilters, lees dan “Passief banddoorlaat RC-filter”.
Outline
Inleiding
Een banddoorlaatfilter is een schakeling die slechts een bepaalde band van frequenties doorlaat. Deze band ligt voornamelijk tussen de afsnijfrequenties fL en fH, waarbij fL de onderste afsnijfrequentie is en fH de bovenste afsnijfrequentie.
De middenfrequentie wordt aangeduid met ‘fC’ en wordt ook wel resonantiefrequentie of piekfrequentie genoemd.
De waarde van fL moet altijd lager zijn dan de waarde van fH. De doorlaatband van het filter is niets anders dan de bandbreedte. De versterking van het filter is maximaal bij de resonantie- of middenfrequentie en dit wordt de totale doorlaatbandversterking genoemd. Deze doorlaatbandversterking wordt aangeduid met “Amax”.
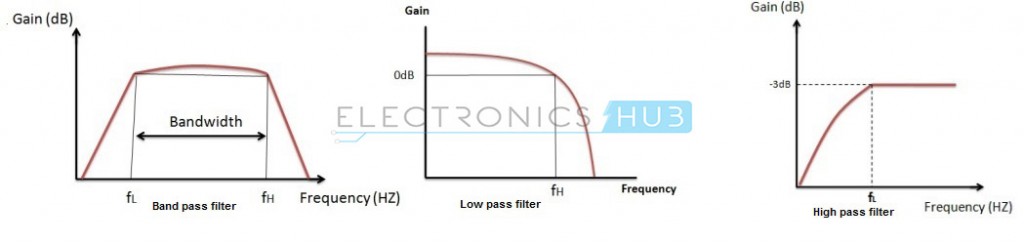
Voor een laagdoorlaatfilter begint deze doorlaatband bij 0 Hz en loopt door tot de waarde van de resonantiefrequentie bij -3 dB vanaf een maximale doorlaatbandversterking.
Zoals bij het hoogdoorlaatfilter deze band begint bij de -3 dB resonantiefrequentie en eindigt bij de waarde van de maximale lusversterking voor het actieve filter. De combinatie van de laagdoorlaat- en hoogdoorlaatresponsies levert de hieronder getoonde banddoorlaatresponsie op:
Terug naar boven
Actief banddoorlaatfilter
Afhankelijk van de kwaliteitsfactor wordt het banddoorlaatfilter ingedeeld in breedbanddoorlaatfilter en smalbanddoorlaatfilter. De kwaliteitsfactor wordt ook wel “figure of merit” genoemd. Door cascadering van hoogdoorlaatfilter en laagdoorlaatfilter met een versterkingscomponent verkrijgen we een banddoorlaatfilter.

De versterkingsschakeling tussen deze hoogdoorlaat- en laagdoorlaatfilters zorgt voor isolatie en geeft over de hele schakeling een spanningsversterking. De waarden van de afsnijfrequenties van beide filters moeten met een minimum verschil worden gehandhaafd.
Als dit verschil erg klein is, bestaat de mogelijkheid dat de hoogdoorlaat- en laagdoorlaatfasen op elkaar inwerken. Om de juiste niveaus van deze afsnijfrequenties te verkrijgen, is dus een versterkingsschakeling nodig.
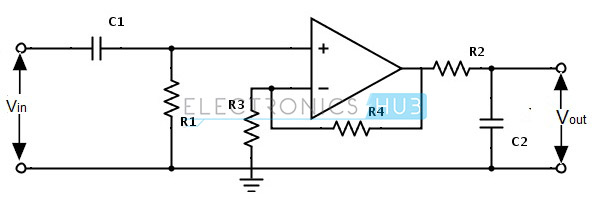
Het schakelschema voor het actieve banddoorlaatfilter is hieronder afgebeeld:
Terug naar boven
Breedbanddoorlaatfilter
Als de waarde van de kwaliteitsfactor kleiner is dan tien, dan is de doorlaatband breed, waardoor we een grotere bandbreedte krijgen. Dit banddoorlaatfilter wordt breedbanddoorlaatfilter genoemd.
In dit filter moet de hoge afsnijfrequentie groter zijn dan de lage afsnijfrequentie. Bij het ontwerp worden twee versterkingselementen (Op-amps) gebruikt.
Eerst gaat het signaal door het hoogdoorlaatfilter, het uitgangssignaal van dit hoogdoorlaatfilter zal naar oneindig neigen en dus wordt het signaal dat naar oneindig neigt aan het eind aan het laagdoorlaatfilter gegeven.
Dit laagdoorlaatfilter zal het hoogfrequente signaal laagdoorlaten.
Wanneer het hoogdoorlaatfilter wordt gecascadeerd met het laagdoorlaatfilter wordt het eenvoudige banddoorlaatfilter verkregen. Om dit filter te realiseren moet de volgorde van de laagdoorlaat- en hoogdoorlaatschakelingen gelijk zijn.
Door een eerste orde laagdoorlaat- en hoogdoorlaatfilter in cascade te schakelen krijgen we een tweede orde banddoorlaatfilter en door twee eerste orde laagdoorlaatfilters in cascade te schakelen met twee hoogdoorlaatfilters ontstaat een vierde orde banddoorlaatfilter.
Door deze cascade te schakelen krijgt de schakeling een lage kwaliteitsfactor. De condensator in het eerste orde hoogdoorlaatfilter blokkeert elke DC biasing van het ingangssignaal.
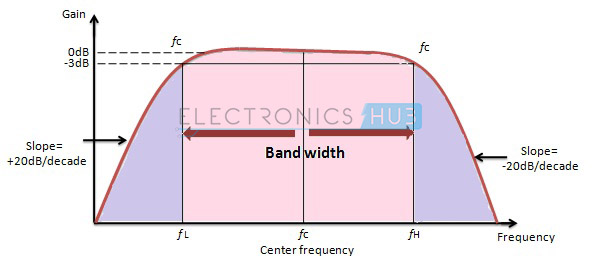
De afrol van de versterking bij beide stopbanden is ± 20 dB /decade in het geval van een tweede orde filter (Hoog + Laag). De hoogdoorlaat- en laagdoorlaatfilters mogen alleen van de eerste orde zijn.
Zo ook, wanneer de hoogdoorlaat- en laagdoorlaatfilters van de tweede orde zijn, dan is de afrol van de versterking op beide stopplaatsen ± 40dB/decade.
De uitdrukking voor de spanningsversterking van het banddoorlaatfilter is als volgt:
| Vout / Vin | = / √{}
Het wordt verkregen door de afzonderlijke versterkingen van zowel het hoogdoorlaat- als het laagdoorlaatfilter, de afzonderlijke versterkingen van zowel het hoogdoorlaat- als het laagdoorlaatfilter zijn hieronder gegeven.
Voltageversterking voor Hoogdoorlaatfilter:
| Vout / Vin | = / √
Voltageversterking voor Laagdoorlaatfilter:
| Vout / Vin | = Amax2 / √
Amax = Amax1 * Amax2
Waarbij Amax1 de versterking is van de hoogdoorlaat trap en Amax2 de versterking van de laagdoorlaat trap.
De respons van het breedbandfilter is hieronder weergegeven.
Terug naar boven
Smalbanddoorlaatfilter
Als de waarde van de kwaliteitsfactor groter is dan tien, is de doorlaatband smal en is de bandbreedte van de doorlaatband ook kleiner. Dit banddoorlaatfilter wordt smalbanddoorlaatfilter genoemd.
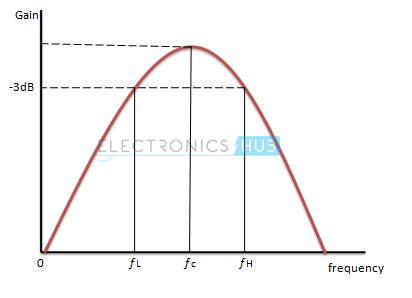
Het gebruikt slechts één actieve component (op-amp) in plaats van twee en deze op-amp is inverterend geconfigureerd. In dit filter is de versterking van de op-amp maximaal bij de middenfrequentie fc.
Terug naar boven
Narrow Band Pass Filter Circuit
De ingang wordt toegepast op de inverterende ingangsaansluiting. Dit toont aan dat de Op-amp in inverterende configuratie is. Deze filterkring produceert een smalbanddoorlaatfilterrespons.

De spanningsversterking van de bovenstaande filterschakeling is AV = – R2 / R1
De afsnijfrequenties van deoff frequenties van de filterkring zijn
fC1 = 1 / (2πR1C1) en fC2 = 1 / (2πR2C2)
Terug naar boven
Multi Feedback Actief Band Pass Filter
Deze filterkring produceert een afgestemde kring op basis van de negatieve terugkoppeling van het filter. Het belangrijke voordeel van deze meervoudige terugkoppeling is dat we zonder enige verandering in de maximale versterking bij de middenfrequentie de waarde van de afsnijfrequentie kunnen veranderen. Deze verandering van de afsnijfrequentie kan worden bewerkstelligd door de weerstand ‘R3’.
Beschouwen we de onderstaande actieve filterschakeling als volgt, beschouwen we de gewijzigde weerstandswaarde als R3′ en de gewijzigde afsnijfrequentie als fc′, dan kunnen we de nieuwe weerstandswaarde als volgt gelijkstellen:
R3′ = R3(fc /fc′)²
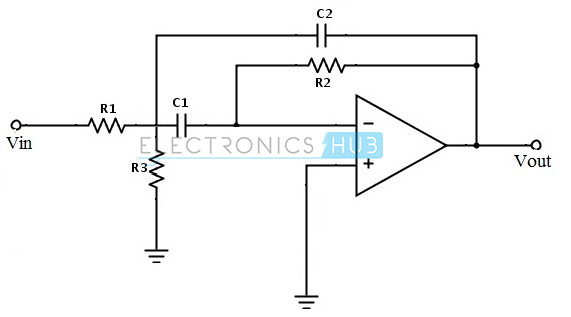
Het bestaat uit twee feedback paden, vanwege deze meervoudige feedback paden wordt het ook wel aangeduid als ‘Multiple feedback band pass circuit’. Deze schakeling produceert een oneindig versterkte meervoudige terugkoppeling banddoorlaatfilter. Door deze schakeling stijgt de kwaliteitsfactor maximaal tot 20.
fc = 1/√(R1R2C1C2)
Q = fc/Bandbreedte = (½){√}
Amax = -R2/2R1
R1 = Q/{2πfcCAmax}
R2 = Q/πfcC
R3 = Q/{2πfcC(2Q² – Amax)}
De versterking bij de centrumfrequentie ‘Amax’ moet kleiner zijn dan 2Q². Dat wil zeggen,
Amax < 2Q²
Waar,
fc = afsnijfrequentie in Hz
C = Capaciteit, (C1 = C2 = C)
Q = Kwaliteitsfactor
Amax = Maximale versterking
Terug naar boven
De frequentierespons van een actief bandfilter
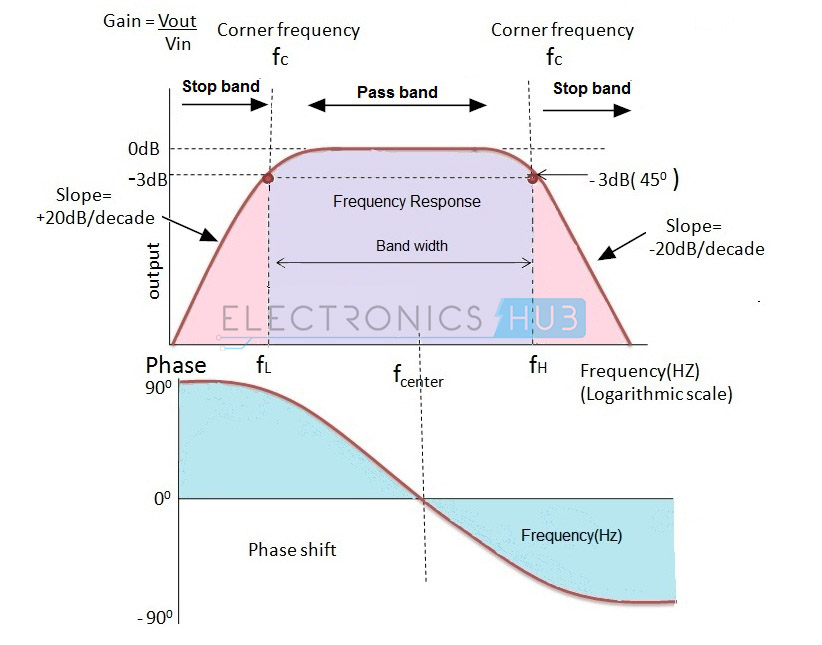
Het heeft twee centrumfrequenties, een van het hoogdoorlaatfilter en de andere van het laagdoorlaatfilter. De middenfrequentie van het hoogdoorlaatfilter moet lager zijn dan de middenfrequentie van het laagdoorlaatfilter.
De middenfrequentie van het banddoorlaatfilter is het meetkundig gemiddelde van de onder- en bovengrens van de afsnijfrequenties fr2 = fH * fL.
De versterking van het filter is 20 log (Vout/Vin) dB/Decade. De amplituderesponsie is vergelijkbaar met de responsies van het laagdoorlaat- en hoogdoorlaatfilter. De responscurve hangt af van de cascadevolgorde van het filter.
De genormaliseerde middenfrequentie is gegeven als fr = 1. Beschouwen we twee afsnijfrequenties, 300 Hz en 900 Hz, dan is de bandbreedte van het filter 300 Hz -900 Hz = 600 Hz.
Terug naar boven
De kwaliteitsfactor
De kwaliteitsfactor is afhankelijk van de bandbreedte van de doorlaatband. De kwaliteitsfactor is omgekeerd evenredig met de bandbreedte. Dat betekent dat als de bandbreedte toeneemt de kwaliteitsfactor afneemt en als de bandbreedte afneemt de kwaliteitsfactor toeneemt.
Q = fc/Bandbreedte
Voor een breedbanddoorlaatfilter is de kwaliteitsfactor laag omdat de doorlaatbandbreedte hoog is. Voor een smalbandig doorlaatfilter is de kwaliteitsfactor hoog. De selectiviteit en niet-selectiviteit hangt af van de breedte van de doorlaatband.
Deze kwaliteitsfactor houdt ook verband met de dempingsfactor (). Als de waarde van de dempingscoëfficiënt hoger is, is ook de vlakheid van de uitgangsresponsie groter. Dit wordt als volgt berekend:
ε = 2/Q
Voor verschillende waarden van de kwaliteitsfactor is de genormaliseerde versterkingsrespons van een tweede-ordebanddoorlaatfilter gegeven als:
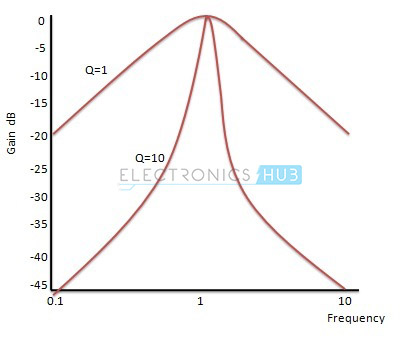
Uit deze grafiek blijkt duidelijk dat de selectiviteit groter is bij een hogere kwaliteitsfactor.
Terug naar boven
Actief banddoorlaatfilter voorbeeld
Laat ons de oneindige meervoudige terugkoppelingsschakeling van het actieve filter beschouwen waarvoor de resonantiefrequentie 1,5 kHz is en de maximale spanningsversterking 15,0 kHz.5 kHz is, de maximale spanningsversterking 15 en de kwaliteitsfactor 7. Dan worden de componentwaarden als volgt berekend:
Voor weerstanden
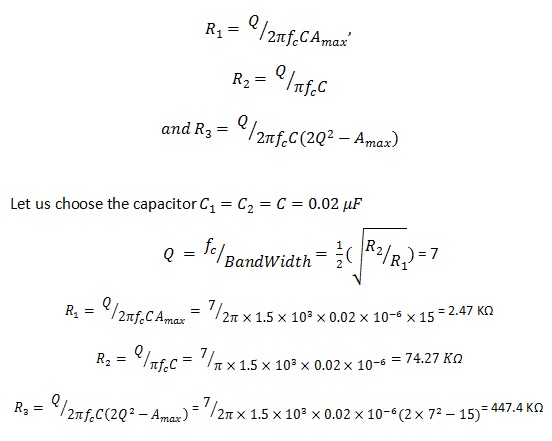
Wij gaan ervan uit dat de gewijzigde weerstandswaarde R3´ is en de gewijzigde afsnijfrequentie fc´=2 KHz, dan kunnen we de nieuwe weerstandswaarde als volgt vergelijken: