Inleiding

Column buckling is een merkwaardig en uniek onderwerp. Het is misschien wel het enige gebied van de constructiemechanica waar bezwijken niet gerelateerd is aan de sterkte van het materiaal. Een knikanalyse van een kolom bestaat uit het bepalen van de maximale belasting die een kolom kan dragen voordat hij bezwijkt. Maar voor lange kolommen heeft het bezwijken niets te maken met de sterkte van het materiaal. In plaats daarvan wordt het bepaald door de stijfheid van de kolom, zowel materieel als geometrisch.
Op deze pagina worden de standaardvergelijkingen voor het knikken van kolommen op twee manieren afgeleid. Eerst wordt de gebruikelijke ontwikkeling van de vergelijkingen behandeld, d.w.z. de Euler Buckling Theorie. Dit is de afleiding die in handboeken staat en in ingenieurscursussen wordt gepresenteerd. Maar ik heb er nooit van gehouden. Niet omdat zij onjuist is (zij is juist), maar omdat ik vind dat zij niet op bevredigende wijze de fysische mechanismen weergeeft die het knikproces beheersen. Daarom wordt ook een tweede afleiding van de knikvergelijkingen gegeven.
Vreemd genoeg worden objecten kolommen genoemd als ze axiaal worden belast, zoals hier het geval is, maar balken als ze dwars worden belast.
Toch staat de balkbuigtheorie centraal bij kolomknikanalyses, dus het is aan te bevelen dat de lezer deze balkbuigpagina doorneemt.
Euler Buckling Theory
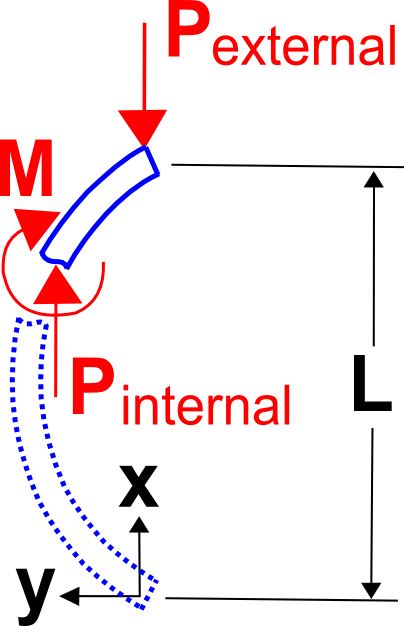
De Euler Buckling Theory is de klassieke theorie die in leerboeken en klaslokalen wordt gepresenteerd. De theorie begint eenvoudig met de constatering dat het interne buigmoment in een belaste en vervormde kolom gelijk is aan -P , y , waarbij -P de drukbelasting is en -Y de doorbuiging van de kolom. Voeg dus \(-P, y\) in voor \(M) in de liggerbuigingsvergelijking, \( E, I, y” = M).
Dit levert de volgende differentiaalvergelijking
die de oplossing heeft
waarbij \(A) en \(B) constanten zijn die bepaald zijn uit de randvoorwaarden.
De randvoorwaarden zijn \(y = 0) bij \(x = 0) en \(x = L).
De eerste randvoorwaarde, \(y = 0) bij \(x = 0), leidt tot de conclusie dat \(B = 0). En dan blijft er over… Tot zover alles goed. Maar op dit punt heeft de klassieke afleiding de neiging om de natuurkundige intuïtie achter zich te laten en openlijk wiskundig te worden…
De dingen worden erg interessant met de tweede randvoorwaarde omdat, zoals we zullen zien, deze niet leidt tot de bepaling van de onbekende constante, nl. Om dit te zien, voegen we de tweede randvoorwaarde als volgt in.
Er zijn hier in principe twee mogelijkheden. In het eerste geval is A = 0, maar dit is saai omdat het leidt tot het resultaat dat alle verschuivingen nul zijn. Dit is gewoon de niet-geknikte oplossing. Voordat de kolom knikt, zijn de zijwaartse verplaatsingen gewoon nul.
Het tweede geval is het interessantste, en het geval dat direct verband houdt met het knikken van de kolom. De tweede methode om aan de randvoorwaarde te voldoen is op te merken dat (\sin(\pi) = 0). De manier om aan de randvoorwaarde te voldoen is dus om te eisen dat het argument in de vergelijking, links( \sqrt{P \over E \, I}} \; L \rechts)\) gelijk moet zijn aan \(\pi).Dit geeft
\en oplossen voor \(P\) geeft
Dit is het klassieke Euler knik-theorie resultaat. Het geeft de kritische waarde van de belasting (P), genaamd P_{cr}), waarboven de kolom zal knikken.
Dit resultaat is volkomen legitiem. Maar, zoals nu wel duidelijk zal zijn, is het erg wiskundig van aard, en levert het weinig natuurkundig inzicht op. De komende afleiding hieronder zal een alternatieve methode voorstellen om tot dezelfde vergelijking te komen, die naar mijn mening een veel directer fysisch verband met het knikproces biedt dan de bovenstaande afleiding deed.

Buckling vs Yielding
Zoals in het begin gezegd, is de klassieke knikanalyse onafhankelijk van de vloeigrens van een materiaal. Dit is duidelijk in de bovenstaande afleiding, omdat op geen enkel moment spanning of rek werd besproken of vergeleken met de sterkte van een materiaal. aar in feite mogen overwegingen betreffende de vloeigrens nooit volledig worden genegeerd. Als men eenmaal een schatting van P(cr) uit bovenstaande vergelijking heeft, moet men deze altijd delen door de doorsnede van de kolom(A) om een spanning
(cr)(cr) te verkrijgen en deze waarde vergelijken met de vloeigrens van het materiaal om te bepalen of er vloeigrens optreedt voordat de kolom bezwijkt. Dit is kritisch voor korte kolommen omdat deze inherent hoge waarden hebben omdat deze in de noemer van de knikvergelijking staan.

End Constraints in Buckling
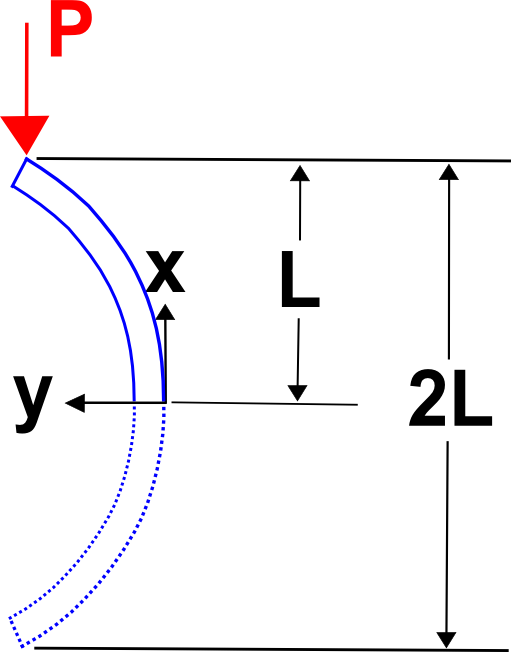
Hoewel niet de focus van deze pagina, is het belangrijk te onderkennen dat eindbeperkingen kritisch zijn voor knikanalyses omdat ze de waarde van P_{cr} wijzigen. Bedenk bijvoorbeeld dat de kritische knikbelasting van de hier getoonde kolom gegeven wordt door ²(P_{cr}}). Merk op dat deze waarde 1/4 is van die in de eerdere vergelijking voor ²(P_{cr}}). Maar het is gemakkelijk te zien waarom. Uit de schets blijkt dat de knikvoorwaarde hier precies gelijk is aan het knikken van een kolom van tweemaal de lengte en met dezelfde randvoorwaarden als in de bovenstaande afleiding. En dit leidt tot
Fysisch-gebaseerde Knikafleiding
In dit deel wordt een alternatieve methode gepresenteerd voor het bepalen van kritische knikbelastingen die volgens mij fysisch intuïtiever is dan de klassieke Euler knikbelastingstheorie. Het belangrijkste kenmerk is de vergelijking van het inwendige buigmoment dat ontstaat door de interne spanningsverdeling met het uitwendige buigmoment dat ontstaat door de op de kolom uitgeoefende belasting. (De vorige zin is kritisch.)
Deze benadering gaat ongeveer verder waar eerder werd opgemerkt dat de klassieke Euler benadering openlijk mathematisch wordt. De eerste stap is het aannemen van een vervormde vorm. We weten dat y = 0 aan beide uiteinden van de kolom, en dat de vorm een functie volgt die gebaseerd is op de abovedifferentiaalvergelijking. De meest logische keuze is dus
waarbij \(\delta_{max}\) de zijdelingse verplaatsing in het midden van de kolom is. De waarde hiervan is onbekend, maar het is bekend dat deze in het midden van de kolom groter is dan in elk ander punt van de kolom, vandaar het subscript \(max}). De keuze van \pi x / L als argument van de functie \(sin()\) zorgt ervoor dat de verplaatsingen nul zijn op \(x = 0) en \(x = L). (Over andere aangenomen vormen zullen we het zo meteen hebben.)

Als je je afvraagt hoe het zit met de term \(\sqrt{P/EI}) in de functie \(\sin()\) uit de eerdere Euler-oplossing, dan hoeft dat niet. Die term komt uit de oplossing van de differentiaalvergelijking, maar we doen hier net alsof we niets weten over de details van die oplossing (uitzonderingsalarm!). We hebben alleen een functie nodig die kan lijken op een gebogen kolom met nul verplaatsingen aan de uiteinden. Met behulp van de functie sin ( {pi x x over L} ) bereiken we dit.
De “uitzonderingswaarschuwing” is hierboven aanwezig omdat we in feite gebruik maken van een stukje kennis over de eerdere analyse. Daarom moeten zoveel mogelijk sinussen en cosinussen worden gebruikt om de vervormde vormen te beschrijven, omdat die leiden tot de nauwkeurigste schattingen van P_{cr}).
Herinner u uit de balkbuigtheorie dat het buigend moment, \(M), gerelateerd is aan de doorbuiging van de kolom door
Hoewel het niet kritisch is, is het nuttig om te onthouden dat deze relatie is ontstaan uit de berekening van het moment in de doorsnede als gevolg van de spanningsverdeling. De relatie laat zien dat we deze tweede afgeleide van de veronderstelde verplaatsingsfunctie nodig hebben.
Dit is het interne buigmoment in de kolom ten gevolge van de spanningsverdeling in de kolom, die op zijn beurt het gevolg is van het feit dat de kolom gebogen is.
Hier komt een belangrijke gedachte… Dit buigend moment kan worden gezien als de interne buigweerstand van de kolom, of de kracht waarmee de kolom probeert weer recht te komen.
De eenvoudige volgende stap is om dit interne weerstandbuigend moment gelijk te stellen aan het buigend moment ten gevolge van de uitwendige belasting. Dat moment is eenvoudig(M = -P, y(x)-). Het is niet moeilijk om nu al te zien dat deze benadering leidt tot dezelfde uitdrukking voor P_{cr} als de klassieke Euler kniktheorie. Maar gaandeweg heeft het veel meer inzicht gegeven in het fysische proces van knikken dan de vroegere theorie.
- We komen tot deze relatie door het inwendige buigmoment (ten gevolge van de inwendige spanningen ten gevolge van de buiging van de kolom) gelijk te stellen aan het uitwendige buigmoment ten gevolge van de uitwendige belasting, \(P\). Het moet duidelijk zijn dat bezwijken optreedt wanneer \(P\) groot genoeg is om aan de vergelijking te voldoen. Als de waarde kleiner is, zal \(P, y(x)\) kleiner zijn dan het “weerstandbuigmoment”.
- Het feit dat \(y(x)\) aan beide zijden van de vergelijking voorkomt, en dus zal worden opgeheven, betekent dat wanneer knik optreedt, dit gelijktijdig over de hele lengte van de kolom gebeurt. (Een fascinerend resultaat dat in de Eulertheorie niet terug te vinden is.)
Hoe dan ook, het wegstrepen van y(x)aan beide zijden van de vergelijking geeft
weer, maar met veel meer natuurkundig inzicht deze keer.

Voorbeeld met vast uiteinde
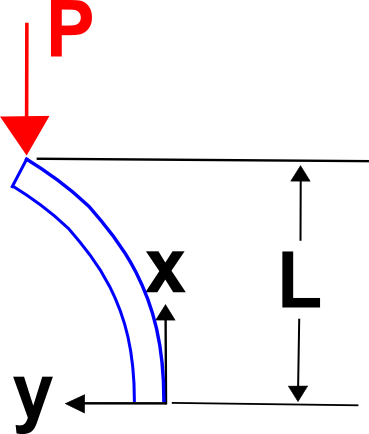
Ga deze keer uit van een vervormde vorm van
Bereken het buigmoment dat hierdoor ontstaat.
Het buigend moment ten gevolge van de uitwendige belasting is M = P ( \delta_{max} – y(x) )²). Door deze twee aan elkaar gelijk te stellen en te vereenvoudigen ontstaat het bekende resultaat.

Voorbeeld van een vast uiteinde met een andere veronderstelde vorm
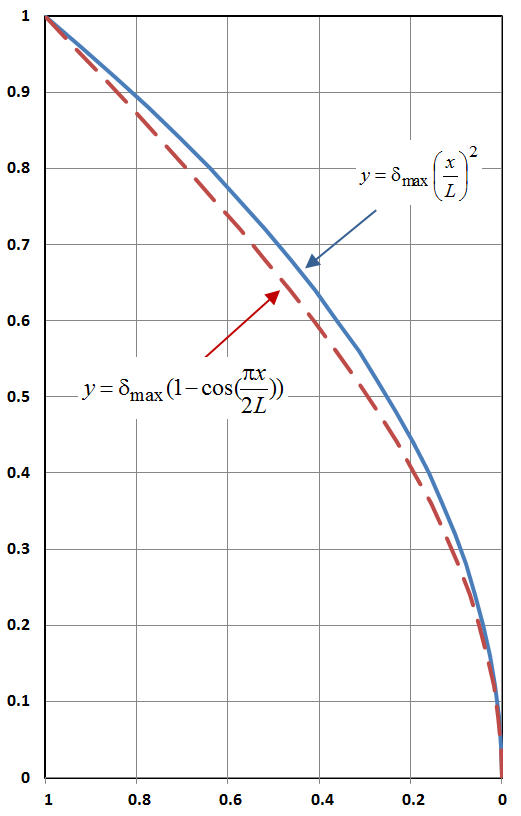
Dit voorbeeld toont aan dat alternatieve functies kunnen worden aangenomen voor de vervormde vorm van de kolom, en dat de resulterende formule voor P_{cr} niet significant zal verschillen van de exacte oplossing.
Vermoed deze keer een vervormde vorm van
Bereken het buigend moment als gevolg hiervan.
Het buigend moment als gevolg van de uitwendige belasting blijft \(M = P ( \delta_{max} – y(x) )²). Het gelijkstellen van deze twee geeft
Het is duidelijk uit de vergelijking dat de minimale waarde van P optreedt bij x = 0, omdat op dit punt y(x) een minimum is (nul in feite) en dus y(\delta_{max} – y(x))is een maximum. Door \(y(x)\) op nul te stellen en \(\delta_{max})\) van beide kanten af te trekken ontstaat
Dit resultaat is natuurlijk niet gelijk aan de exacte oplossing hierboven. Het verschil is dat de exacte oplossing 2,467% bevat, terwijl deze benaderende oplossing 2,23% verschil bevat. Significant, maar niet groot zoals, laten we zeggen, een factor 2, of een orde van grootte. Merk ook op dat de benaderende oplossing conservatief is, omdat zij een kritieke knikbelasting geeft die lager is dan die van de exacte oplossing.
Het is interessant op te merken dat deze oplossing, gebaseerd op de kwadratische vorm, leidde tot een lagere kritieke knikbelasting en een concentratie van de knikfalen aan de basis van de kolom, (x = 0).De exacte oplossing met de trig-functie daarentegen, gaf een gelijke knikneiging over de hele lengte van de kolom, en een overeenkomstige hogere P_{cr}.
Het belangrijkste hierbij is dat de veronderstelde kwadratische vervormingsvorm geen exacte oplossing van de regerende differentiaalvergelijking is (hoewel hij er dichtbij ligt). Trigfuncties zijn dat wel.