Hoi Glenn,

Ik ga ervan uit dat je te maken hebt met een regelmatige achthoek.

Eerst moet je weten hoeveel diagonalen een regelmatige achthoek heeft en vervolgens hoeveel de langste lengte hebben. Teken een octagon, kies een hoekpunt en construeer elke diagonaal vanuit dit hoekpunt.Je zult zien dat er 5 van zulke diagonalen zijn.

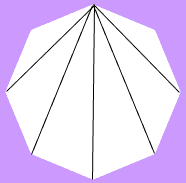
Dus voor elk van de 8 hoekpunten kun je 5 diagonalen tekenen en dus heb je 5 8 = 40 diagonalen geconstrueerd. Maar je hebt elke diagonaal twee keer geconstrueerd, één keer vanuit elk van zijn uiteinden. Er zijn dus 20 diagonalen in een regelmatige achthoek.

Als je naar het diagram hierboven kijkt, zie je dat een van de geconstrueerde diagonalen langer is dan de andere. Je construeert dus een lange diagonaal vanuit elk hoekpunt, en dus 8 lange diagonalen. Opnieuw heb je elke diagonaal twee keer geconstrueerd, dus zijn er 4 lange diagonalen. Dus als je één diagonaal kiest uit alle diagonalen in een regelmatige achthoek, heb je 4 kansen op 20 dat je één van de langste kiest, en dus een kans van 4/20 = 1/5.

Hoe zit het met de kortste?

Andrei en Penny