Laatst bijgewerkt op 25 september 2019

In plaats van de klassewaarden direct te voorspellen voor een classificatieprobleem, kan het handig zijn om de waarschijnlijkheid te voorspellen dat een observatie tot elke mogelijke klasse behoort.

Het voorspellen van waarschijnlijkheden biedt enige flexibiliteit, waaronder het beslissen hoe de waarschijnlijkheden moeten worden geïnterpreteerd, het presenteren van voorspellingen met onzekerheid, en het bieden van meer genuanceerde manieren om de vaardigheid van het model te evalueren.

Voorspelde waarschijnlijkheden die overeenkomen met de verwachte verdeling van de waarschijnlijkheden voor elke klasse worden gekalibreerd genoemd. Het probleem is dat niet alle machine learning modellen in staat zijn om gekalibreerde kansen te voorspellen.

Er zijn methoden om zowel te diagnosticeren hoe gekalibreerd de voorspelde kansen zijn als om de voorspelde kansen beter te kalibreren met de waargenomen verdeling van elke klasse. Vaak kan dit leiden tot kwalitatief betere voorspellingen, afhankelijk van hoe de vaardigheid van het model wordt geëvalueerd.

In deze tutorial ontdekt u het belang van het kalibreren van voorspelde kansen en hoe u de kalibratie van modellen die worden gebruikt voor probabilistische classificatie kunt diagnosticeren en verbeteren.

Na afloop van deze tutorial weet u:

• Nonlineaire machine learning-algoritmen voorspellen vaak niet-gekalibreerde klassenwaarschijnlijkheden.
• Betrouwbaarheidsdiagrammen kunnen worden gebruikt om de kalibratie van een model te diagnosticeren, en methoden kunnen worden gebruikt om de voorspellingen voor een probleem beter te kalibreren.
• Hoe je betrouwbaarheidsdiagrammen ontwikkelt en classificatiemodellen kalibreert in Python met scikit-learn.

Kick-start je project met mijn nieuwe boek Probability for Machine Learning, inclusief stap-voor-stap tutorials en de Python broncodebestanden voor alle voorbeelden.

Laten we beginnen.

Hoe en wanneer een gekalibreerd classificatiemodel gebruiken met scikit-learn
Foto door Nigel Howe, sommige rechten voorbehouden.

Tutorial Overzicht

Deze tutorial is onderverdeeld in vier delen; deze zijn:

1. Voorspellen van waarschijnlijkheden
2. Kalibreren van voorspellingen
3. Hoe waarschijnlijkheden te kalibreren in Python
4. Werkvoorbeeld van het kalibreren van SVM waarschijnlijkheden

Voorspellen van waarschijnlijkheden

Een classificatie voorspellend modelleringsprobleem vereist het voorspellen of voorspellen van een label voor een gegeven observatie.

Een alternatief voor het direct voorspellen van het label, kan een model de waarschijnlijkheid voorspellen dat een waarneming bij elk mogelijk class label hoort.

Dit biedt enige flexibiliteit, zowel in de manier waarop voorspellingen worden geïnterpreteerd en gepresenteerd (keuze van drempelwaarde en voorspellingsonzekerheid) als in de manier waarop het model wordt geëvalueerd.

Hoewel een model in staat kan zijn kansen te voorspellen, kan het zijn dat de verdeling en het gedrag van de kansen niet overeenkomen met de verwachte verdeling van waargenomen kansen in de trainingsdata.

Dit komt vooral voor bij complexe niet-lineaire machine learning-algoritmen die niet direct probabilistische voorspellingen doen, maar in plaats daarvan benaderingen gebruiken.

De verdeling van de waarschijnlijkheden kan worden aangepast om beter overeen te komen met de verwachte verdeling die in de gegevens is waargenomen. Deze aanpassing wordt kalibratie genoemd, zoals in de kalibratie van het model of de kalibratie van de verdeling van de klassenwaarschijnlijkheden.

we willen dat de geschatte klassenwaarschijnlijkheden een afspiegeling zijn van de werkelijke onderliggende waarschijnlijkheid van de steekproef. Dat wil zeggen, de voorspelde klassikale kans (of kans-achtige waarde) moet goed gekalibreerd zijn. Om goed gekalibreerd te zijn, moeten de kansen effectief de ware waarschijnlijkheid van de gebeurtenis van belang weerspiegelen.

– Pagina 249, Applied Predictive Modeling, 2013.

Kalibratie van voorspellingen

Er zijn twee aandachtspunten bij het kalibreren van kansen; dat zijn het diagnosticeren van de kalibratie van voorspelde kansen en het kalibratieproces zelf.

Betrouwbaarheidsdiagrammen (kalibratiecurves)

Een betrouwbaarheidsdiagram is een lijnplot van de relatieve frequentie van wat is waargenomen (y-as) versus de voorspelde waarschijnlijkheidsfrequentie (x-as).

Betrouwbaarheidsdiagrammen zijn gangbare hulpmiddelen om de eigenschappen van probabilistische voorspellingssystemen te illustreren. Ze bestaan uit een plot van de waargenomen relatieve frequentie tegen de voorspelde waarschijnlijkheid, en bieden een snelle visuele vergelijking bij het afstemmen van probabilistische voorspellingssystemen, en documenteren de prestaties van het eindproduct

– Increasing the Reliability of Reliability Diagrams, 2007.

Specifiek worden de voorspelde waarschijnlijkheden opgedeeld in een vast aantal buckets langs de x-as. Vervolgens wordt voor elke bak het aantal gebeurtenissen (klasse=1) geteld (d.w.z. de relatieve waargenomen frequentie). Tenslotte worden de tellingen genormaliseerd.

Deze plots worden in de prognoseliteratuur doorgaans “betrouwbaarheidsdiagrammen” genoemd, maar kunnen ook “kalibratieplots” of “-curven” worden genoemd, omdat ze aangeven hoe goed de prognosemogelijkheden zijn gekalibreerd.

Hoe beter een prognose is gekalibreerd of hoe betrouwbaarder deze is, hoe dichter de punten langs de hoofddiagonaal van linksonder naar rechtsboven op de plot liggen.

De positie van de punten of de curve ten opzichte van de diagonaal kan helpen bij de interpretatie van de waarschijnlijkheden; bijvoorbeeld:

• Onder de diagonaal: Het model heeft overvoorspeld; de waarschijnlijkheden zijn te groot.
• Boven de diagonaal: Het model heeft te laag voorspeld; de waarschijnlijkheden zijn te klein.

Waarschijnlijkheden zijn per definitie continu, dus verwachten we enige afwijking van de lijn, vaak weergegeven als een S-vormige curve met pessimistische neigingen tot overvoorspelling van lage waarschijnlijkheden en ondervoorspelling van hoge waarschijnlijkheden.

Betrouwbaarheidsdiagrammen bieden een diagnostiek om na te gaan of de voorspelde waarde Xi betrouwbaar is. Grofweg is een waarschijnlijkheidsvoorspelling betrouwbaar als de gebeurtenis daadwerkelijk plaatsvindt met een waargenomen relatieve frequentie die consistent is met de voorspelde waarde.

-Betrouwbaarheid van betrouwbaarheidsdiagrammen vergroten, 2007.

Het betrouwbaarheidsdiagram kan helpen om de relatieve kalibratie van de voorspellingen van verschillende voorspellingsmodellen te begrijpen.

Probabiliteitskalibratie

De voorspellingen die een voorspellend model doet, kunnen worden gekalibreerd.

Gekalibreerde voorspellingen kunnen (al dan niet) resulteren in een verbeterde kalibratie op een betrouwbaarheidsdiagram.

Sommige algoritmen zijn zodanig gefit dat hun voorspelde waarschijnlijkheden al gekalibreerd zijn. Zonder in detail te treden waarom, logistische regressie is zo’n voorbeeld.

Andere algoritmen produceren niet direct voorspellingen van kansen, en in plaats daarvan moet een voorspelling van kansen worden benaderd. Enkele voorbeelden zijn neurale netwerken, support vector machines, en beslisbomen.

De voorspelde kansen van deze methoden zullen waarschijnlijk niet gekalibreerd zijn en kunnen baat hebben bij een aanpassing via kalibratie.

Kalibratie van voorspellingskansen is een herschaling die wordt toegepast nadat de voorspellingen zijn gedaan door een voorspellend model.

Er zijn twee populaire benaderingen voor het kalibreren van kansen; dat zijn de Platt Scaling en Isotonic Regression.

Platt Scaling is eenvoudiger en is geschikt voor betrouwbaarheidsdiagrammen met de S-vorm. Isotonic Regression is complexer, vereist veel meer gegevens (anders kan het overfit), maar kan betrouwbaarheidsdiagrammen met verschillende vormen ondersteunen (is niet-parametrisch).

Platt Scaling is het meest effectief als de vervorming in de voorspelde waarschijnlijkheden sigmoïde-vormig is. Isotone regressie is een krachtigere kalibratiemethode die elke monotone vervorming kan corrigeren. Helaas heeft deze extra kracht een prijs. Een leercurve-analyse laat zien dat Isotone Regressie vatbaarder is voor overfitting, en dus slechter presteert dan Platt Scaling, wanneer de gegevens schaars zijn.

– Predicting Good Probabilities With Supervised Learning, 2005.

Note, en dit is echt belangrijk: beter gekalibreerde waarschijnlijkheden kunnen wel of niet leiden tot betere klasse- of waarschijnlijkheids-gebaseerde voorspellingen. Het hangt echt af van de specifieke metriek die wordt gebruikt om voorspellingen te evalueren.

In feite suggereren sommige empirische resultaten dat de algoritmen die het meest kunnen profiteren van het kalibreren van voorspelde waarschijnlijkheden SVMs, bagged decision trees, en random forests zijn.

na kalibratie zijn de beste methoden boosted trees, random forests en SVMs.

– Predicting Good Probabilities With Supervised Learning, 2005.

Hoe kansberekeningen te kalibreren in Python

Met de scikit-learn machine learning bibliotheek kunt u zowel een diagnose stellen van de kansberekening van een classifier als een classifier kalibreren die kansberekeningen kan voorspellen.

Kalibratie diagnosticeren

U kunt de kalibratie van een classifier diagnosticeren door een betrouwbaarheidsdiagram te maken van de werkelijke kansen versus de voorspelde kansen op een testset.

In scikit-learn wordt dit een kalibratiecurve genoemd.

Dit kan worden geïmplementeerd door eerst de kalibratie_curve() functie te berekenen. Deze functie neemt de ware klasse-waarden voor een dataset en de voorspelde waarschijnlijkheden voor de hoofdklasse (=1). De functie retourneert de ware kansen voor elke bin en de voorspelde kansen voor elke bin. Het aantal bins kan worden opgegeven met het n_bins argument en is standaard 5.

Hieronder staat bijvoorbeeld een stukje code dat het gebruik van de API laat zien:

1 2 3 4 5 6 7 8 9 10

… # voorspel waarschijnlijkheden probs = model.predic_proba(testX) # betrouwbaarheidsdiagram fop, mpv = calibration_curve(testy, probs, n_bins=10) # plot perfect gekalibreerd pyplot.plot(, , linestyle=’–‘) # plot model betrouwbaarheid pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

Kalibreer classifier

Een classifier kan in scikit-learn worden gekalibreerd met behulp van de klasse CalibratedClassifierCV.

Er zijn twee manieren om deze klasse te gebruiken: prefit en cross-validatie.

U kunt een model fitten op een training dataset en dit prefit model kalibreren met behulp van een hold-out validatie dataset.

Hieronder staat bijvoorbeeld een stukje code dat het gebruik van de API laat zien:

1 2 3 4 5 6 7 8 9 10 11 12 13

… # gegevens voorbereiden trainX, trainy = … valX, valy = … testX, testy = … # fit base model on training dataset model = … model.fit(trainX, trainy) # kalibreer model op validatiegegevens calibrator = CalibratedClassifierCV(model, cv=’prefit’) calibrator.fit(valX, valy) # evalueer het model yhat = calibrator.predict(testX)

Bij wijze van alternatief kan de CalibratedClassifierCV meerdere exemplaren van het model fitten met behulp van k-voudige kruisvalidatie en de door deze modellen voorspelde waarschijnlijkheden kalibreren met behulp van de hold-out set. Voorspellingen worden gedaan met behulp van elk van de getrainde modellen.

Hieronder staat bijvoorbeeld een stukje code dat het gebruik van de API laat zien:

1 2 3 4 5 6 7 8 9 10 11

… # gegevens voorbereiden trainX, trainy = … testX, testy = … # definieer basismodel model = … # fit en calibreer model op trainingsdata calibrator = CalibratedClassifierCV(model, cv=3) calibrator.fit(trainX, trainy) # evalueer het model yhat = calibrator.predict(testX)

De klasse CalibratedClassifierCV ondersteunt twee soorten waarschijnlijkheidskalibratie; namelijk de parametrische ‘sigmoid’-methode (methode van Platt) en de niet-parametrische ‘isotonic’-methode die kan worden opgegeven via het argument ‘methode’.

Werkvoorbeeld van het kalibreren van SVM-kansen

We kunnen de discussie over kalibratie concreet maken met enkele werkvoorbeelden.

In deze voorbeelden passen we een support vector machine (SVM) toe op een ruisachtig binair classificatieprobleem en gebruiken we het model om waarschijnlijkheden te voorspellen, vervolgens bekijken we de kalibratie met behulp van een betrouwbaarheidsdiagram en kalibreren we de classificator en bekijken we het resultaat.

SVM is een goed model om te kalibreren omdat het van nature geen waarschijnlijkheden voorspelt, wat betekent dat de waarschijnlijkheden vaak niet gekalibreerd zijn.

Een opmerking over SVM: waarschijnlijkheden kunnen worden voorspeld door de decision_function() functie op het fit model aan te roepen in plaats van de gebruikelijke predict_proba() functie. De waarschijnlijkheden zijn niet genormaliseerd, maar kunnen worden genormaliseerd bij het aanroepen van de calibration_curve() functie door het ‘normalize’ argument op ‘True’ te zetten.

Het onderstaande voorbeeld past een SVM model op het testprobleem, voorspelt de kansen, en plot de kalibratie van de kansen als een betrouwbaarheidsdiagram,

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

# SVM-betrouwbaarheidsdiagram from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # genereer 2 klasse dataset X, y = make_classification(n_samples=1000, n_klassen=2, gewichten=, random_state=1) # splitsen in train/test sets trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # fit een model model = SVC() model.fit(trainX, trainy) # voorspellen waarschijnlijkheden probs = model.decision_function(testX) # betrouwbaarheidsdiagram fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot perfect gekalibreerd pyplot.plot(, , linestyle=’–‘) # plot model betrouwbaarheid pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

Het uitvoeren van het voorbeeld creëert een betrouwbaarheidsdiagram dat de kalibratie toont van de SVM’s voorspelde waarschijnlijkheden (ononderbroken lijn) in vergelijking met een perfect gekalibreerd model langs de diagonaal van de plot (onderbroken lijn.)

We zien de verwachte S-vormige curve van een conservatieve voorspelling.

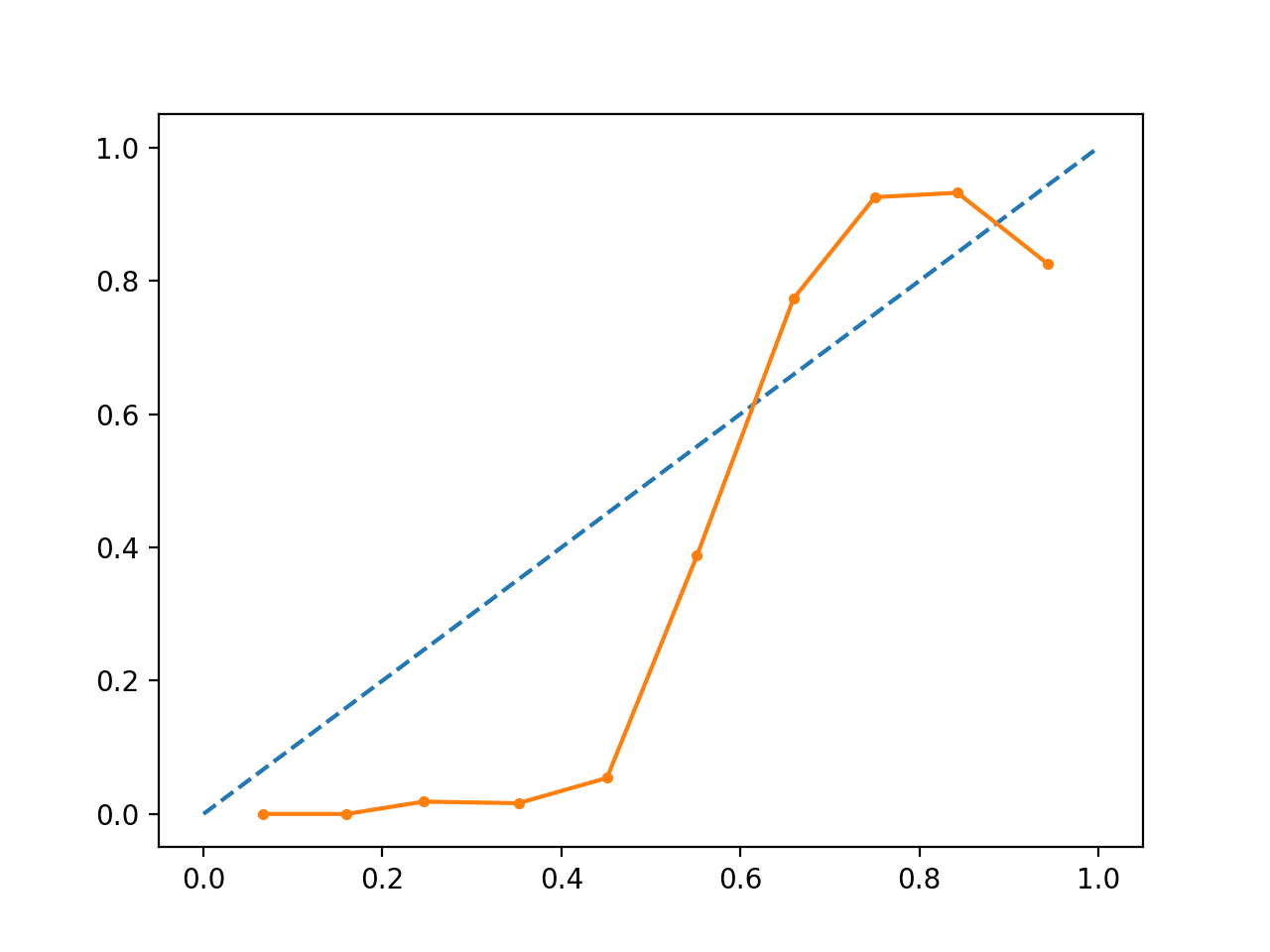
Ongekalibreerd SVM Betrouwbaarheidsdiagram

We kunnen het voorbeeld bijwerken om het SVM te fitten via de CalibratedClassifierCV klasse met 5-voudige kruisvalidatie, waarbij we de holdout sets gebruiken om de voorspelde waarschijnlijkheden te kalibreren.

Het volledige voorbeeld staat hieronder.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

# SVM-betrouwbaarheidsdiagram met kalibratie from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # genereer 2 klasse dataset X, y = make_classification(n_samples=1000, n_klassen=2, gewichten=, random_state=1) # splitsen in train/test sets trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # fit een model model = SVC() calibrated = CalibratedClassifierCV(model, method=’sigmoid’, cv=5) calibrated.fit(trainX, trainy) # voorspel waarschijnlijkheden probs = calibrated.predict_proba(testX) # betrouwbaarheidsdiagram fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot perfect gecalibreerd pyplot.plot(, , linestyle=’–‘) # plot gekalibreerde betrouwbaarheid pyplot.plot(mpv, fop, marker=’.’) pyplot.show()

Het uitvoeren van het voorbeeld creëert een betrouwbaarheidsdiagram voor de gekalibreerde waarschijnlijkheden.

De vorm van de gekalibreerde waarschijnlijkheden is anders, ze volgen de diagonale lijn veel beter, hoewel ze in het bovenste kwadrant nog steeds te laag voorspellen.

Visueel suggereert de plot een beter gekalibreerd model.

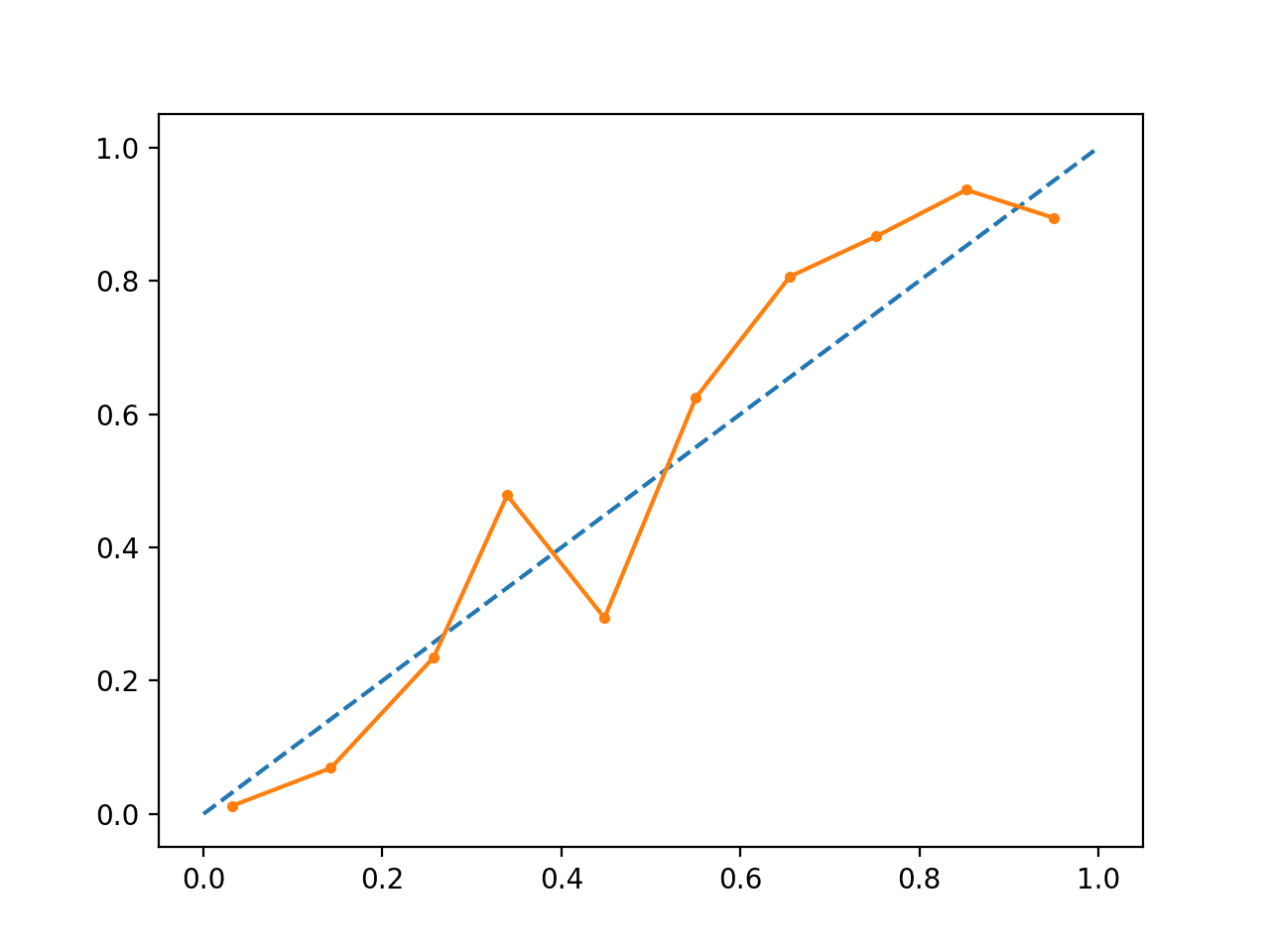
Gekalibreerd SVM Betrouwbaarheidsdiagram

We kunnen het contrast tussen de twee modellen duidelijker maken door beide betrouwbaarheidsdiagrammen in dezelfde plot op te nemen.

Het volledige voorbeeld staat hieronder.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

# SVM-betrouwbaarheidsdiagrammen met ongekalibreerde en gekalibreerde waarschijnlijkheden from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot #voorspel ongecalibreerde waarschijnlijkheden def uncalibrated(trainX, testX, trainy): # fit een model model = SVC() model.fit(trainX, trainy) # predict probabilities return model.decision_function(testX) # predict calibrated probabilities def calibrated(trainX, testX, trainy): # definieer model model = SVC() # definieer en fit kalibratiemodel gekalibreerd = GekalibreerdeClassifierCV(model, method=’sigmoid’, cv=5) gekalibreerd.fit(trainX, trainy) # voorspel waarschijnlijkheden return gekalibreerd.predict_proba(testX) # genereer dataset van 2 klassen X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # splitsing in train/test sets trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # ongekalibreerde voorspellingen yhat_uncalibrated = ongekalibreerd(trainX, testX, trainy) # gekalibreerde voorspellingen yhat_gekalibreerd = gekalibreerd(trainX, testX, trainy) # betrouwbaarheidsdiagrammen fop_ongecalibreerd, mpv_ongekalibreerd = kalibratie_curve(testy, yhat_ongekalibreerd, n_bins=10, normalize=True) fop_gekalibreerd, mpv_gekalibreerd = kalibratie_curve(testy, yhat_gekalibreerd, n_bins=10) # plot perfect gekalibreerd pyplot.plot(, , linestyle=’–‘, color=’black’) # plot modelbetrouwbaarheden pyplot.plot(mpv_ongekalibreerd, fop_ongekalibreerd, marker=’.’) pyplot.plot(mpv_gekalibreerd, fop_gekalibreerd, marker=’.’) pyplot.show()

Het uitvoeren van het voorbeeld levert één betrouwbaarheidsdiagram op dat zowel de gekalibreerde (oranje) als de ongekalibreerde (blauwe) waarschijnlijkheden toont.

Het is niet echt een vergelijking van appels met appels, aangezien de voorspellingen van het gekalibreerde model in feite een combinatie van vijf submodellen zijn.

Niettemin zien we een duidelijk verschil in de betrouwbaarheid van de gekalibreerde kansen (zeer waarschijnlijk veroorzaakt door het kalibratieproces).

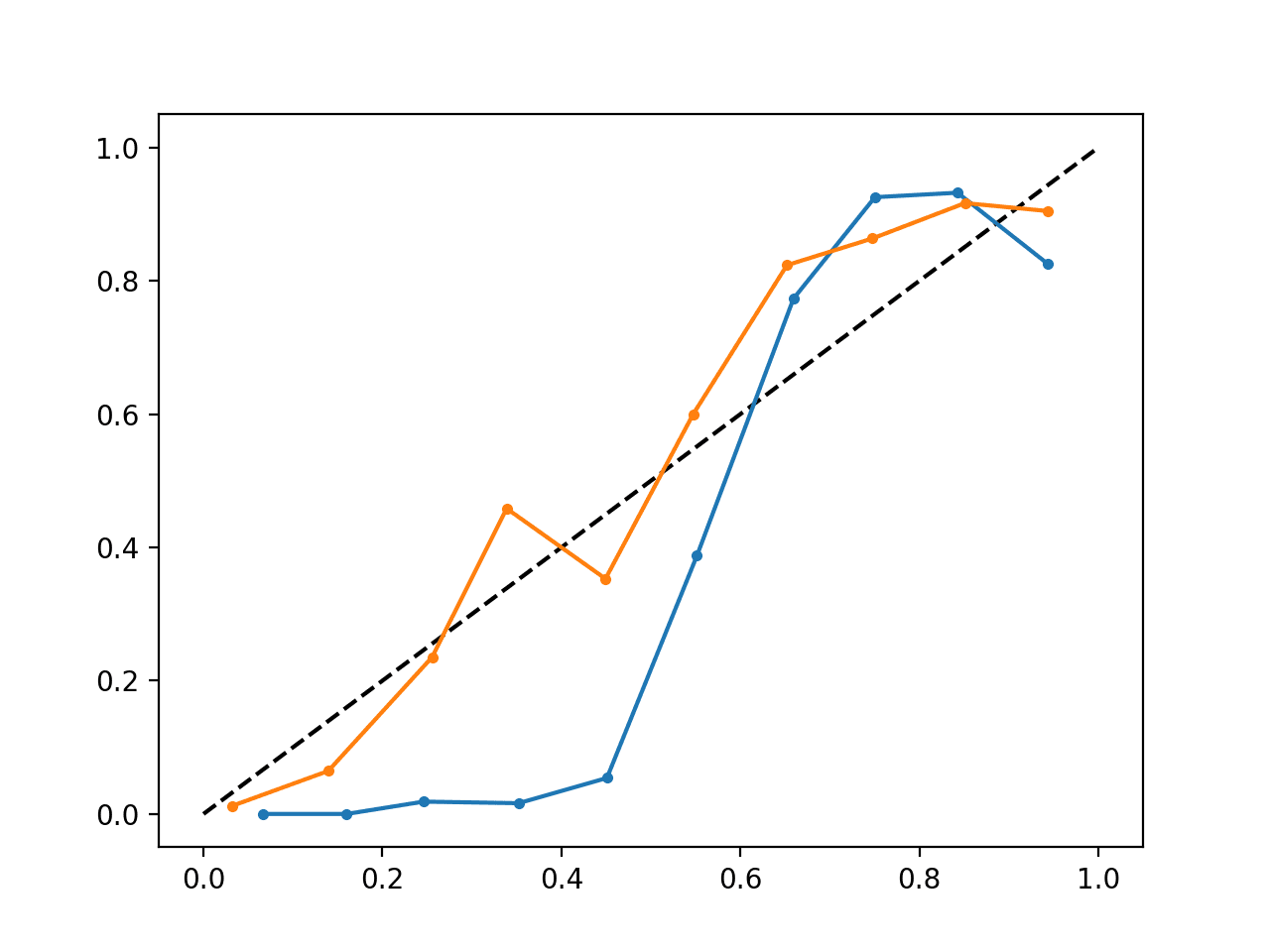
Gekalibreerd en Niet-gekalibreerd SVM Betrouwbaarheidsdiagram

Verder lezen

In deze sectie vind je meer bronnen over dit onderwerp als je dieper op de materie in wilt gaan.

Boeken en papers

• Applied Predictive Modeling, 2013.
• Predicting Good Probabilities With Supervised Learning, 2005.
• Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers, 2001.
• Het verhogen van de betrouwbaarheid van betrouwbaarheidsdiagrammen, 2007.

API

• sklearn.calibration.CalibratedClassifierCV API
• sklearn.calibration.calibration_curve API
• Probability calibration, scikit-learn User Guide
• Probability Calibration curves, scikit-learn
• Vergelijking van calibratie van classifiers, scikit-learn

Artikelen

• CAWCAR Verificatie Website
• Calibratie (statistiek) op Wikipedia
• Probabilistische classificatie op Wikipedia
• Scikit correcte manier om classifiers te kalibreren met CalibratedClassifierCV op CrossValidated

Summary

In deze tutorial, heb je ontdekt hoe belangrijk het is om voorspelde kansen te kalibreren en hoe je de kalibratie van modellen die worden gebruikt voor probabilistische classificatie kunt vaststellen en verbeteren.

In het bijzonder hebt u geleerd:

• Nonlineaire machine learning-algoritmen voorspellen vaak niet-gekalibreerde klassenwaarschijnlijkheden.
• Betrouwbaarheidsdiagrammen kunnen worden gebruikt om de kalibratie van een model te diagnosticeren, en methoden kunnen worden gebruikt om voorspellingen voor een probleem beter te kalibreren.
• Hoe je betrouwbaarheidsdiagrammen ontwikkelt en classificatiemodellen kalibreert in Python met scikit-learn.

Heb je nog vragen?
Stel je vragen in de reacties hieronder en ik zal mijn best doen om ze te beantwoorden.

Krijg grip op kansberekening voor Machine Learning!

Ontwikkel uw inzicht in kansberekening

…met slechts een paar regels python code

Ontdek hoe in mijn nieuwe Ebook:
Probability for Machine Learning

Het biedt zelfstudie tutorials en end-to-end projecten over:
Bayes Theorem, Bayesian Optimization, Distributions, Maximum Likelihood, Cross-Entropy, Calibrating Models
en nog veel meer.

Haal eindelijk de onzekerheid uit uw projecten

Schuif de academici over boord. Zie wat er in staat

Tweet Share Share