Familywise Error Rates > Holm-Bonferroni Methode

Je wilt misschien eerst dit artikel lezen: Familywise Error Rates.

Wat is de Holm-Bonferroni Methode?

De Holm-Bonferroni Methode (ook wel Holm’s Sequential Bonferroni Procedure genoemd) is een manier om met familywise error rates (FWER) voor meervoudige hypothesetests om te gaan. Het is een wijziging van de Bonferroni-correctie. De Bonferroni-correctie vermindert de kans op een statistisch significant resultaat (d.w.z. een Type I-fout) bij het uitvoeren van meervoudige tests. Hoewel de Bonferroni eenvoudig te berekenen is, lijdt zij aan een gebrek aan statistisch vermogen. De Holm-Bonferroni-methode is ook vrij eenvoudig te berekenen, maar is krachtiger dan de Bonferroni in één stap.

Formule

De formule om de Holm-Bonferroni te berekenen is: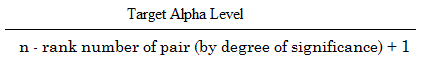

Waar:

• Doel alfa-niveau = algemeen alfa-niveau (meestal .05),
• n = aantal tests.

Het volgende voorbeeld laat zien hoe de formule werkt.

Voorbeeld

Vraag: Gebruik de Holm-Bonferroni-methode om de volgende vier hypothesen en hun bijbehorende p-waarden te toetsen bij een alfaniveau van .05:

• H1 = 0.01.
• H2 = 0.04
• H3 = 0.03
• H4 = 0.005

Opgelet: we kennen al de p-waarden die bij elke hypothese horen. Als u de p-waarden niet kent, voer dan voor elke hypothese een test uit voordat u FWER probeert aan te passen met de Holm-Bonferroni-methode.

Stap 1: Rangschik de p-waarden van klein naar groot:

• H4 = 0.005
• H1 = 0.01
• H3 = 0.03
• H2 = 0.04

Stap 2: Werk de Holm-Bonferroni formule uit voor de eerste rang:
HB = Doel α / (n – rang + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Stap 3: Vergelijk de eerst gerangschikte (kleinste) p-waarde uit Stap 1 met het alpha niveau berekend in Stap 2:
Kleinste p-waarde, in Stap 1 (H4 = 0.005) < Alfaniveau in Stap 2 (.0125).
Als de p-waarde kleiner is, verwerp dan de nulhypothese voor deze individuele test.

De p-waarde van .005 is kleiner dan .0125, dus de nulhypothese voor H4 wordt verworpen.

Stap 4: Herhaal de HB-formule voor de tweede rang .
HB = Doel α / (n – rang + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

Step 5: Vergelijk het resultaat van de HB formule in Stap 4 met de p-waarde van de tweede rang:
De als tweede gerangschikte p-waarde, in Stap 1 (H1 = 0.01) < Alfaniveau in Stap 2 (.0167).
De p-waarde van .01 is kleiner dan .0167, dus de nulhypothese voor H1 wordt ook verworpen.

Stap 6: Herhaal de HB formule voor de derde rang.
HB = Doel α / (n – rang + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

Stap 7: Vergelijk het resultaat van de HB formule in Stap 6 met de p-waarde van de derde rang:
De derde rang p-waarde, in Stap 1 (H3 = 0.03) > Alfaniveau in Stap 6 (.025).
De p-waarde van .03 is groter dan .025, dus de nulhypothese voor H3 wordt niet verworpen.

De toetsing stopt als je de eerste niet-verworpen hypothese bereikt. Alle volgende hypothesen zijn niet-significant (d.w.z. niet verworpen).

Referentie:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70

——————————————————————————

Heb je hulp nodig bij een huiswerk of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!