Dit is een vector:

Een vector heeft magnitude (grootte) en richting:
De lengte van de lijn geeft de magnitude aan en de pijlpunt wijst in de richting.
We kunnen twee vectoren optellen door ze kop aan staart samen te voegen:
En het maakt niet uit in welke volgorde we ze optellen, we krijgen hetzelfde resultaat:
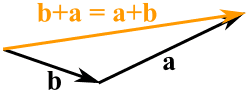
Voorbeeld: Een vliegtuig vliegt met de neus naar het noorden, maar de wind komt uit het noordwesten.
De twee vectoren (de snelheid veroorzaakt door de propeller, en de snelheid van de wind) resulteren in een iets lagere grondsnelheid in de richting van iets ten oosten van het noorden.
Als je het vliegtuig vanaf de grond zou bekijken, lijkt het een beetje zijwaarts te glijden.
Heb je dat ooit zien gebeuren? Misschien hebt u vogels gezien die tegen een sterke wind in worstelen en zijwaarts lijken te vliegen. Vectoren helpen dat te verklaren.
Velociteit, versnelling, kracht en vele andere dingen zijn vectoren.
Aftrekken
We kunnen ook een vector van een andere vector aftrekken:
- eerst keren we de richting van de vector die we willen aftrekken om,
- dan tellen we ze zoals gewoonlijk op:
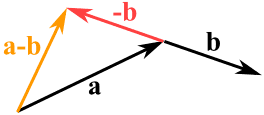
a – b
Notatie
Een vector wordt vaak vetgedrukt geschreven, zoals a of b.
| Een vector kan ook worden geschreven als de letters van zijn kop en staart met een pijltje erboven, zoals dit: |
 |
Berekeningen
Nu …. hoe doen we de berekeningen?
De meest gebruikelijke manier is om vectoren eerst op te splitsen in x- en y-delen, zoals dit:
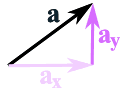
De vector a wordt opgedeeld in
de twee vectoren ax en ay
(We zien later hoe we dit moeten doen.)
Vectoren optellen
We kunnen dan vectoren optellen door de x-delen op te tellen en de y-delen op te tellen:
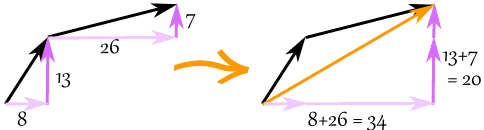
De vector (8, 13) en de vector (26, 7) tellen op tot de vector (34, 20)
Voorbeeld: tel de vectoren a = (8, 13) en b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Wanneer we een vector op die manier opbreken, heet elk deel een component:
Vectoren aftrekken
Om af te trekken, keren we eerst de vector die we willen aftrekken om, en dan voegen we toe.
Voorbeeld: k = (4, 5) aftrekken van v = (12, 2)
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
Magnitude van een vector
De magnitude van een vector wordt weergegeven door twee verticale balken aan weerszijden van de vector:
|a|
Of het kan geschreven worden met dubbele verticale balken (om het niet te verwarren met absolute waarde):
|a||
We gebruiken de stelling van Pythagoras om hem te berekenen:
|a| = √( x2 + y2 )
Voorbeeld: wat is de magnitude van de vector b = (6, 8) ?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Een vector met magnitude 1 heet een Eenheidsvector.
Vector vs Scalar
Een scalar heeft alleen magnitude (grootte).
Scalar: gewoon een getal (zoals 7 of -0,32) .. zeker geen vector.
Een vector heeft magnitude en richting, en wordt vaak vet geschreven, zodat we weten dat het geen scalair is:
- zo c is een vector, het heeft magnitude en richting
- maar c is gewoon een waarde, zoals 3 of 12.4
Voorbeeld: kb is eigenlijk de scalaire k maal de vector b.
Vermenigvuldiging van een vector met een scalaire
Wanneer we een vector met een scalaire vermenigvuldigen, noemen we dat “schalen” van een vector, omdat we veranderen hoe groot of klein de vector is.
Voorbeeld: vermenigvuldig de vector m = (7, 3) met de scalar 3
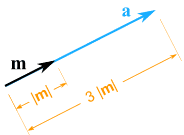 |
a = 3m = (3×7, 3×3) = (21, 9) |
Het wijst nog steeds in dezelfde richting, maar is 3 keer zo lang
(En nu weet je waarom getallen “scalars” worden genoemd, omdat ze de vector omhoog of omlaag “schalen”.)
Vermenigvuldiging van een vector met een vector (Stipproduct en Kruisproduct)
 |
Hoe vermenigvuldigen we twee vectoren met elkaar? Er is meer dan één manier!
(Lees deze pagina’s voor meer details.) |
Meer dan 2 dimensies
Vectoren werken ook prima in 3 of meer dimensies:
De vector (1, 4, 5)
Voorbeeld: tel de vectoren a = (3, 7, 4) en b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Voorbeeld: wat is de magnitude van de vector w = (1, -2, 3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9) = √14
Hier volgt een voorbeeld met 4 dimensies (maar het is moeilijk te tekenen!):
Voorbeeld: trek (1, 2, 3, 4) af van (3, 3, 3, 3)
(3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3) + (-1,-2,-3,-4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Grootte en richting
We kunnen de magnitude en richting van een vector weten, maar we willen de x- en y-lengte (of omgekeerd):
 |
<> |  |
| Vector a in pool coördinaten |
Vector a in Cartesische Coordinaten |
Hoe je ze moet omrekenen kun je lezen bij Poolse en Cartesische Coordinaten, maar hier is een korte samenvatting:
| Van Poolcoördinaten (r,θ) naar Cartesische Coördinaten (x,y) |
Van Cartesische Coördinaten (x,y) naar Poolcoördinaten (r,θ) |
|
|---|---|---|
|
|
Een voorbeeld
Sam en Alex trekken aan een doos.
- Sam trekt met 200 Newton kracht onder een hoek van 60°
- Alex trekt met 120 Newton kracht onder een hoek van 45° zoals weergegeven
Wat is de gecombineerde kracht, en de richting ervan?
Laten we de twee vectoren kop aan staart optellen:
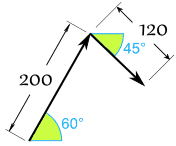
Eerst omrekenen van polair naar Cartesiaans (naar 2 decimalen):
Sams vector:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0,8660 = 173.21
Alex’s Vector:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0.7071 = 84.85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84,85
Nu hebben we:
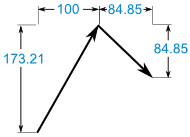
Tel ze bij elkaar op:
(100, 173,21) + (84,85, -84,85) = (184.85, 88.36)
Dit antwoord is geldig, maar laten we terugrekenen naar polair, want de vraag was in polair:
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88,36 / 184,85 ) = 25.5°
En we hebben dit (afgeronde) resultaat: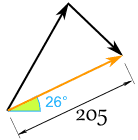
En zo ziet het er voor Sam en Alex uit:
Ze zouden misschien een beter resultaat krijgen als ze schouder aan schouder stonden!





