قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).
Definitie
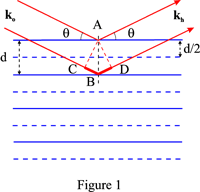
De wet van Bragg geeft de voorwaarde voor een vlakke golf om te worden afgebogen door een familie van roostervlakken:
2 d sin θ = n λ
waarbij d de interplanaire afstand is, θ de hoek tussen de golfvector van de invallende vlakke golf, ko, en de roostervlakken, λ de golflengte en n een geheel getal, de orde van de reflectie. Zij is equivalent aan de diffractievoorwaarde in de reciproke ruimte en aan de vergelijkingen van Laue.
Directe afleiding van de wet van Bragg
- Weerspiegeling uit het eerste vlak
De verstrooide golven zullen in fase zijn, ongeacht de verdeling van de puntverstrooiers in het eerste vlak, indien de hoek van de gereflecteerde golfvector, kh, ook gelijk is aan θ. Dit is de wet van Snell-Descartes van de weerkaatsing.
- Reflectie vanuit het tweede vlak
Omdat de fase van de gereflecteerde golven onafhankelijk is van de positie van de puntverstrooier in het vlak, wordt het faseverschil tussen de door twee opeenvolgende roosteroppervlakken gereflecteerde golven verkregen door willekeurig een verstrooiingspunt, A, op het eerste vlak en een verstrooiingspunt, B, op het tweede vlak zo te kiezen dat AB loodrecht op de vlakken staat. Indien C en D de projecties zijn van A op de invallende en weerkaatste golfvectoren die door B gaan, blijkt uit figuur 1 dat het padverschil tussen de in A en B weerkaatste golven respectievelijk is:
CB + BD = 2d sin θ
en dat de twee golven in fase zullen zijn als dit padverschil gelijk is aan nλ, waarbij n een geheel getal is.
- Reflectie van het derde, enz. vlak
Als voor de eerste twee vlakken aan de relatie van Bragg is voldaan, zullen de met golfvector kh gereflecteerde golven voor alle vlakken van de familie in fase zijn.
Rangorde van de reflectie
De wet van Bragg kan ook worden geschreven:
2 (d/n) sin θ = λ.
Dan kan men zeggen dat een Bragg-reflectie van orde n op een familie van roostervlakken van orde n gelijkwaardig is aan een reflectie van orde 1 op een familie van fictieve, of denkbeeldige, vlakken met roosterafstand
d_{hkl} = d/n.
Deze fictieve familie is geassocieerd met de reciproke roostervector OH waarbij OH = n/d = 1/d_{hkl}. De indexen van de reflecties zijn hkl. Zo komen de gestippelde horizontale lijnen in figuur 1 overeen met de fictieve vlakken geassocieerd met de tweede orde, n = 2.
Reflectieomstandigheden
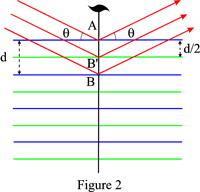
Als er een glijvlak of een schroefas loodrecht op de roostervlakken is, is de afstand tussen de eigenlijke reflecterende vlakken d/2 voor een glijvlak en (d p/q) voor een qp-schroefas. De wet van Bragg moet dan worden geschreven:
2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ
voor een glijvlak en
2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ
voor een schroefas qp.
De reflecties van oneven orde voor een glijvlak en van orde verschillend van (q/p)n voor een schroefas zijn dan afwezig. Men spreekt van systematische afwezigheden in verband met de aanwezigheid van glij- of schroefcomponenten.
Als voorbeeld toont figuur 2 het geval van een 21 schroefas: de spiegelende vlakken zijn de blauwe vlakken en de groene vlakken die door de werking van de schroefas uit de laatste worden afgeleid. Reflecties van oneven orde zullen systematisch afwezig zijn.
Invloed van vervorming
Een vervorming die een familie van roostervlakken (hkl) onvervormd laat en de roosterafstand d onveranderd laat, zal geen invloed hebben op de Bragghoek van kkl reflecties, bijv.b.v. roostervlakken evenwijdig aan een schroef dislocaties.
Geschiedenis
Bragg (1890-1971) presenteerde zijn afleiding van de reflectievoorwaarde op een bijeenkomst van de Cambridge Philosophical Society op 11 november 1912. Zijn artikel werd in 1913 gepubliceerd. Voor details, zie P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Section 5, p. 64 en A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Section 6.11, p. 120.
Zie ook
- Laue-vergelijkingen